|
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that curve. The evolute of a circle is therefore a single point at its center. Equivalently, an evolute is the envelope of the normals to a curve. The evolute of a curve, a surface, or more generally a submanifold, is the caustic of the normal map. Let be a smooth, regular submanifold in . For each point in and each vector , based at and normal to , we associate the point . This defines a Lagrangian map, called the normal map. The caustic of the normal map is the evolute of . Evolutes are closely connected to involutes: A curve is the evolute of any of its involutes. History Apollonius ( 200 BC) discussed evolutes in Book V of his ''Conics''. However, Huygens is sometimes credited with being the first to study them (1673). Huygen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve. It is a class of curves coming under the roulette family of curves. The evolute of an involute is the original curve. The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled '' Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673). Involute of a parameterized curve Let \vec c(t),\; t\in _1,t_2 be a regular curve in the plane with its curvature nowhere 0 and a\in (t_1,t_2), then the curve with the parametric representation \vec C_a(t)=\vec c(t) -\frac\; \int_a^t, \vec c'(w), \; dw is an ''involute'' of the given curve. Adding an arbitrary but fixed number l_0 to the integral \Bigl(\int_a^t, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of all time and a major figure in the Scientific Revolution. In physics, Huygens made groundbreaking contributions in optics and mechanics, while as an astronomer he is chiefly known for his studies of the rings of Saturn and the discovery of its moon Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, a breakthrough in timekeeping and the most accurate timekeeper for almost 300 years. An exceptionally talented mathematician and physicist, Huygens was the first to idealize a physical problem by a set of mathematical parameters, and the first to fully mathematize a mechanistic explanation of an unobservable physical phenomenon.Dijksterhuis, F.J. (2008) Stevin, Huygens and the Dutch re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (curve)
In the geometry of plane curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature, and some authors define a vertex to be more specifically a local extremum of curvature. However, other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant. For space curves, on the other hand, a vertex is a point where the torsion vanishes. Examples A hyperbola has two vertices, one on each branch; they are the closest of any two points lying on opposite branches of the hyperbola, and they lie on the principal axis. On a parabola, the sole vertex lies on the axis of symmetry and in a quadratic of the form: :ax^2 + bx + c\,\! it can be found by completing the square or by differentiation., p. 127. On an ellipse, two of the four vertices lie on the major axis and two lie on the minor axis. For a circle, which has constant curvature, every point is a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Osculating Circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve infinitesimally close to ''p''. Its center lies on the inner normal line, and its curvature defines the curvature of the given curve at that point. This circle, which is the one among all tangent circles at the given point that approaches the curve most tightly, was named ''circulus osculans'' (Latin for "kissing circle") by Leibniz. The center and radius of the osculating circle at a given point are called center of curvature and radius of curvature of the curve at that point. A geometric construction was described by Isaac Newton in his '' Principia'': Nontechnical description Imagine a car moving along a curved road on a vast flat plane. Suddenly, at one point along the road, the steering wheel locks in its present position. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Osculating Circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve infinitesimally close to ''p''. Its center lies on the inner normal line, and its curvature defines the curvature of the given curve at that point. This circle, which is the one among all tangent circles at the given point that approaches the curve most tightly, was named ''circulus osculans'' (Latin for "kissing circle") by Leibniz. The center and radius of the osculating circle at a given point are called center of curvature and radius of curvature of the curve at that point. A geometric construction was described by Isaac Newton in his '' Principia'': Nontechnical description Imagine a car moving along a curved road on a vast flat plane. Suddenly, at one point along the road, the steering wheel locks in its present position. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astroid
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by :x^ + y^ = a^. \, This implies that an astroid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid Osculating Circle Evolute 2
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician Jo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
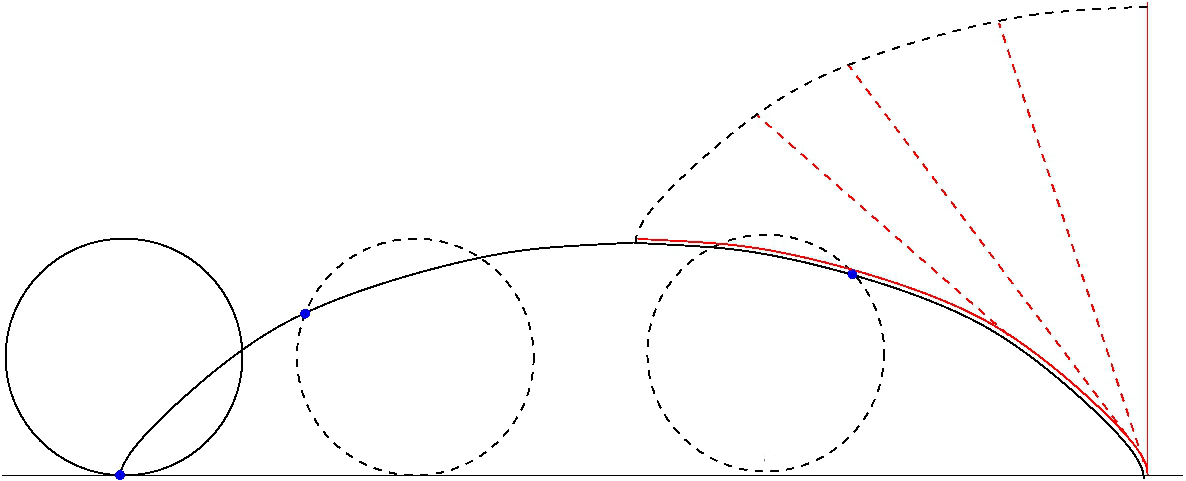
Tait–Kneser Theorem
In differential geometry, the Tait–Kneser theorem states that, if a smooth plane curve has monotonic curvature, then the osculating circles of the curve are disjoint and nested within each other. The logarithmic spiral or the pictured Archimedean spiral provide examples of curves whose curvature is monotonic for the entire curve. This monotonicity cannot happen for a simple closed curve (by the four-vertex theorem, there are at least four vertices where the curvature reaches an extreme point) but for such curves the theorem can be applied to the arcs of the curves between its vertices. The theorem is named after Peter Tait, who published it in 1896, and Adolf Kneser, who rediscovered it and published it in 1912. Tait's proof follows simply from the properties of the evolute, the curve traced out by the centers of osculating circles. For curves with monotone curvature, the arc length along the evolute between two centers equals the difference in radii of the corresponding cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semicubic Parabola
In mathematics, a cuspidal cubic or semicubical parabola is an algebraic plane curve that has an implicit equation of the form : y^2 - a^2 x^3 = 0 (with ) in some Cartesian coordinate system. Solving for leads to the ''explicit form'' : y = \pm a x^, which imply that every real point satisfies . The exponent explains the term ''semicubical parabola''. (A parabola can be described by the equation .) Solving the implicit equation for yields a second ''explicit form'' :x = \left(\frac\right)^. The parametric equation : \quad x = t^2, \quad y = a t^3 can also be deduced from the implicit equation by putting t = \frac. . The semicubical parabolas have a cuspidal singularity; hence the name of ''cuspidal cubic''. The arc length of the curve was calculated by the English mathematician William Neile and published in 1657 (see section History). Properties of semicubical parabolas Similarity Any semicubical parabola (t^2,at^3) is similar to the ''semicubical unit parabola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonius Of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today. Gottfried Wilhelm Leibniz stated “He who understands Archimedes and Apollonius will admire less the achievements of the foremost men of later times.” Apollonius worked on numerous other topics, including astronomy. Most of this work has not survived, where exceptions are typically fragments referenced by other authors like Pappus of Alexandria. His hypothesis of eccentric orbits to explain the apparently aberrant motion of the planets, commonly believed until the Middle Ages, was superseded during the Renaissance. The Apollon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Curve
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of '' parallel (straight) lines''. It can also be defined as a curve whose points are at a constant '' normal distance'' from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not. In computer-aided design the preferred term for a parallel curve is offset curve. (In other geometric contexts, the term offset can also refer to translation.) Offset curves are important for example in numerically controlled machining, where they describe for example the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point. In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |