|
Astroid
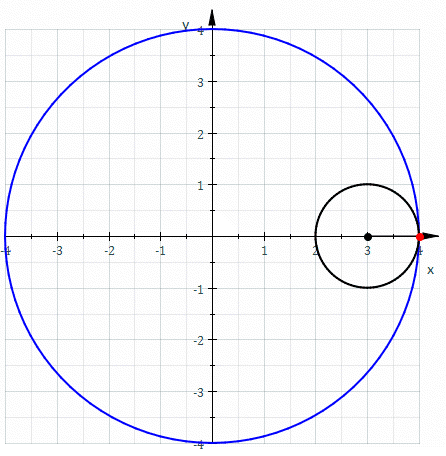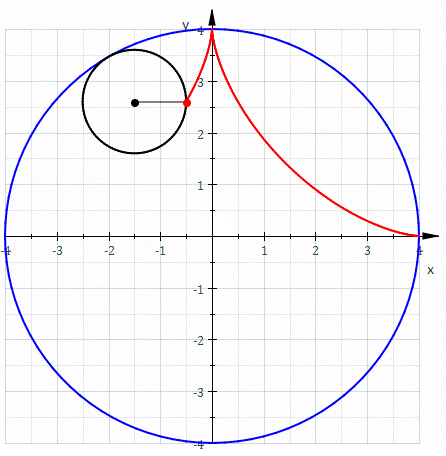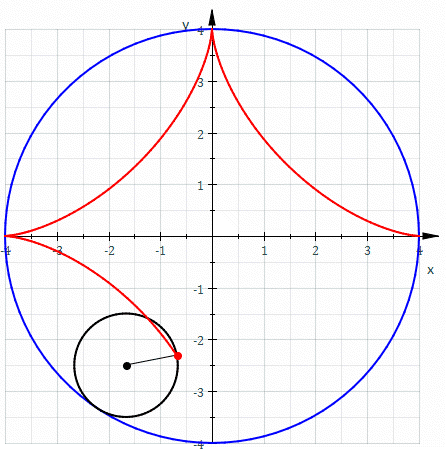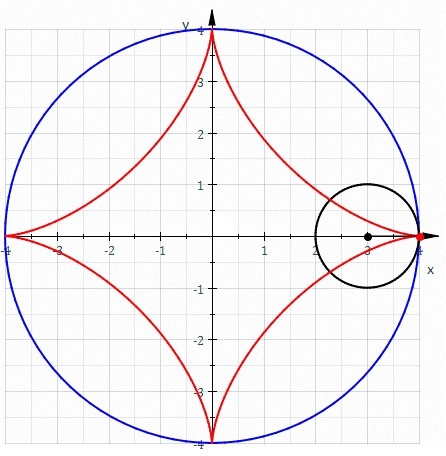
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by :x^ + y^ = a^. \, This implies that an astroid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astroid
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by :x^ + y^ = a^. \, This implies that an astroid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astroid Created With Elipses With A Plus B Const
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for " star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by :x^ + y^ = a^. \, This implies that an astroid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
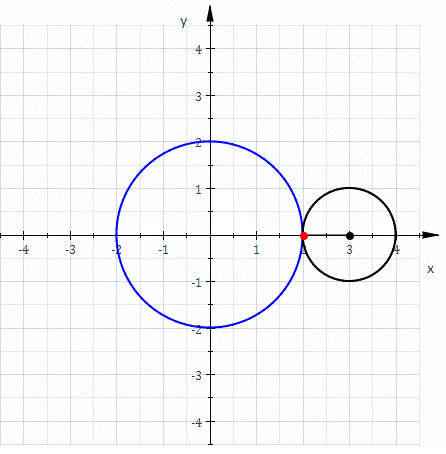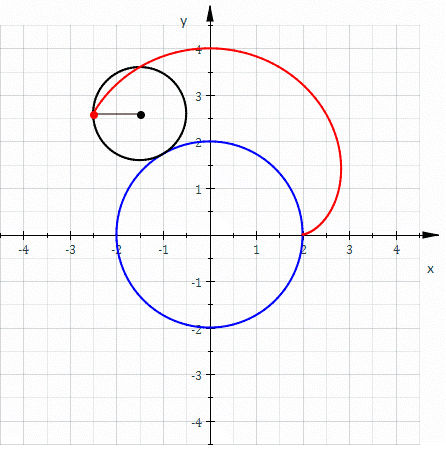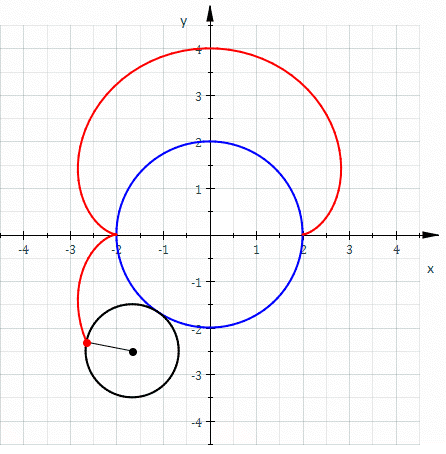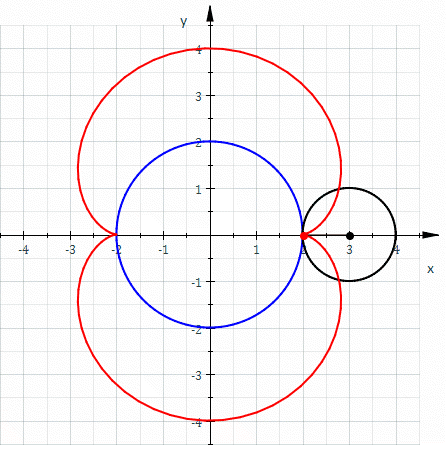
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. Properties If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & y (\theta) = (R - r) \sin \theta - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k - 1) \cos \theta + r \cos \left( (k - 1) \theta \right) \\ & y (\theta) = r (k - 1) \sin \theta - r \sin \left( (k - 1) \theta \right) \end If is an integer, then the curve is closed, and has cusps (i.e., sharp corners, where the curve is not differentiable). Specially for the curve is a straight line and the circles are called Cardano circles. Girolamo Cardano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipse
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape. In the Cartesian coordinate system, the set of all points (x,y) on the curve satisfy the equation :\left, \frac\^n\!\! + \left, \frac\^n\! = 1, where n,a and b are positive numbers, and the vertical bars around a number indicate the absolute value of the number. Specific cases This formula defines a closed curve contained in the rectangle −''a'' ≤ ''x'' ≤ +''a'' and −''b'' ≤ ''y'' ≤ +''b''. The parameters ''a'' and ''b'' are called the ''semi-diameters'' of the curve. The overall shape of the curve is determined by the value of the exponent ''n'', as shown in the following table: If ''n'' 2, a hyperellipse. When ''n'' ≥ 1 and ''a'' = ''b'', the superellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stoner–Wohlfarth Astroid
In magnetism the Stoner– Wohlfarth astroid curve is a curve that separates regions with two minima of the free energy density from those with only one energy minimum. It is a geometric representation of the Stoner–Wohlfarth model. This curve is of particular importance as discontinuous changes of the magnetization can take place when crossing it. One important property of the astroid is that tangents to the astroid represent magnetization directions with extremal energy, i.e. either local minima or local maxima. For a system with a uniaxial anisotropy the tangent(s) that are closest to the easy axis lead to stable solutions, i.e. minimal energy. History The astroid solution was first proposed by John P. Slonczewski in an unpublished IBM research memorandum. It has been extended to single-domain magnets with more general two-dimensional magnetic anisotropy In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hedgehog (geometry)
In differential geometry, a hedgehog or plane hedgehog is a type of plane curve, the envelope of a family of lines determined by a support function. More intuitively, sufficiently well-behaved hedgehogs are plane curves with one tangent line in each oriented direction. A projective hedgehog is a restricted type of hedgehog, defined from an anti-symmetric support function, and (again when sufficiently well-behaved) forms a curve with one tangent line in each direction, regardless of orientation. Every closed strictly convex curve, the envelope of its supporting lines. The astroid forms a non-convex hedgehog, and the deltoid curve forms a projective hedgehog. Hedgehogs can also be defined from support functions of hyperplanes in higher dimensions. Definitions Formally, a planar support function can be defined as a continuously differentiable function h from the unit circle in the plane to real numbers, or equivalently as a function f(\theta)=h\bigl((\cos\theta,\sin\theta)\bigr) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltoid Curve
In geometry, a deltoid curve, also known as a tricuspoid curve or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three or one-and-a-half times its radius. It is named after the capital Greek letter delta (Δ) which it resembles. More broadly, a ''deltoid'' can refer to any closed figure with three vertices connected by curves that are concave to the exterior, making the interior points a non-convex set. Equations A hypocycoid can be represented (up to rotation and translation) by the following parametric equations :x=(b-a)\cos(t)+a\cos\left(\fracat\right) \, :y=(b-a)\sin(t)-a\sin\left(\fracat\right) \, , where ''a'' is the radius of the rolling circle, ''b'' is the radius of the circle within which the aforementioned circle is rolling. (In the illustration above ''b = 3a'' tracing the deltoid.) In complex coordinates this b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pedal Equation
For a plane curve ''C'' and a given fixed point ''O'', the pedal equation of the curve is a relation between ''r'' and ''p'' where ''r'' is the distance from ''O'' to a point on ''C'' and ''p'' is the perpendicular distance from ''O'' to the tangent line to ''C'' at the point. The point ''O'' is called the ''pedal point'' and the values ''r'' and ''p'' are sometimes called the ''pedal coordinates'' of a point relative to the curve and the pedal point. It is also useful to measure the distance of ''O'' to the normal p_c (the ''contrapedal coordinate'') even though it is not an independent quantity and it relates to (r,p) as p_c:=\sqrt . Some curves have particularly simple pedal equations and knowing the pedal equation of a curve may simplify the calculation of certain of its properties such as curvature. These coordinates are also well suited for solving certain type of force problems in classical mechanics and celestial mechanics. Equations Cartesian coordinates For ''C'' given in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette Curve
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this case, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cusp (singularity)
In mathematics, a cusp, sometimes called spinode in old texts, is a point on a curve where a moving point must reverse direction. A typical example is given in the figure. A cusp is thus a type of singular point of a curve. For a plane curve defined by an analytic, parametric equation :\begin x &= f(t)\\ y &= g(t), \end a cusp is a point where both derivatives of and are zero, and the directional derivative, in the direction of the tangent, changes sign (the direction of the tangent is the direction of the slope \lim (g'(t)/f'(t))). Cusps are ''local singularities'' in the sense that they involve only one value of the parameter , in contrast to self-intersection points that involve more than one value. In some contexts, the condition on the directional derivative may be omitted, although, in this case, the singularity may look like a regular point. For a curve defined by an implicit equation :F(x,y) = 0, which is smooth, cusps are points where the terms of lowest de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinate System
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the ''pole'', and the ray from the pole in the reference direction is the ''polar axis''. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. Angles in polar notation are generally expressed in either degrees or radians (2 rad being equal to 360°). Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-17th century, though the actual term "polar coordinates" has been attributed to Gregorio Fontana in the 18th century. The initial motivation for the introduction of the polar system was the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nephroid
In geometry, a nephroid () is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger by a factor of one-half. Name Although the term ''nephroid'' was used to describe other curves, it was applied to the curve in this article by Richard A. Proctor in 1878. Strict definition A nephroid is * an algebraic curve of degree 6. * an epicycloid with two cusps * a plane simple closed curve = a Jordan curve Equations Parametric If the small circle has radius a, the fixed circle has midpoint (0,0) and radius 2a, the rolling angle of the small circle is 2\varphi and point (2a,0) the starting point (see diagram) then one gets the parametric representation: :x(\varphi) = 3a\cos\varphi- a\cos3\varphi=6a\cos\varphi-4a \cos^3\varphi \ , :y(\varphi) = 3a \sin\varphi - a\sin3\varphi =4a\sin^3\varphi\ , \qquad 0\le \varphi < 2\pi The complex map maps the unit circle to a nephroid [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |