Involute on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 For the second type, consider the curve . The arc from to is of length , and the tangent at has angle . Thus, the involute starting from at distance has parametric formulaExpand it up to order , we obtainwhich is a cusp of order 5/2. Explicitly, one may solve for the polynomial expansion satisfied by :or which clearly shows the cusp shape.
Setting , we obtain the involute passing the origin. It is special as it contains no cusp. By serial expansion, it has parametric equationor
For the second type, consider the curve . The arc from to is of length , and the tangent at has angle . Thus, the involute starting from at distance has parametric formulaExpand it up to order , we obtainwhich is a cusp of order 5/2. Explicitly, one may solve for the polynomial expansion satisfied by :or which clearly shows the cusp shape.
Setting , we obtain the involute passing the origin. It is special as it contains no cusp. By serial expansion, it has parametric equationor
 For a circle with parametric representation , one has
.
Hence , and the path length is .
Evaluating the above given equation of the involute, one gets
:
for the
For a circle with parametric representation , one has
.
Hence , and the path length is .
Evaluating the above given equation of the involute, one gets
:
for the 
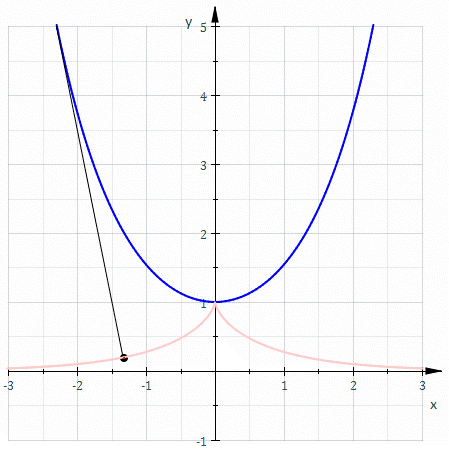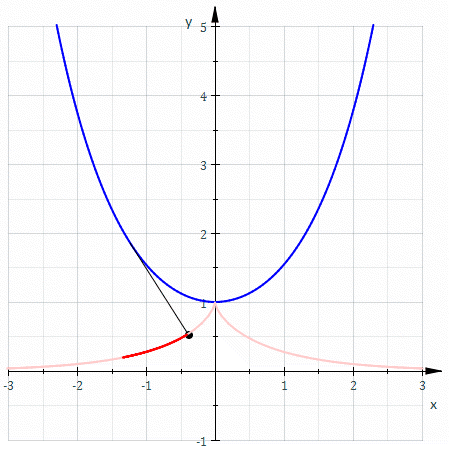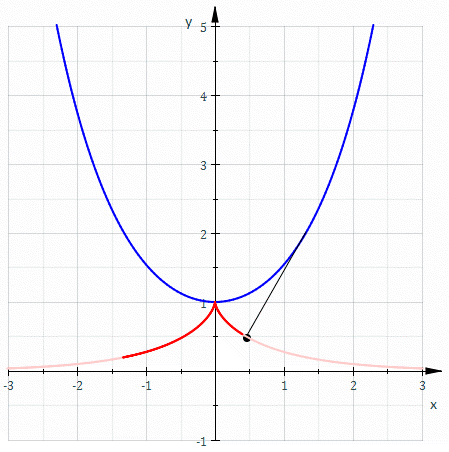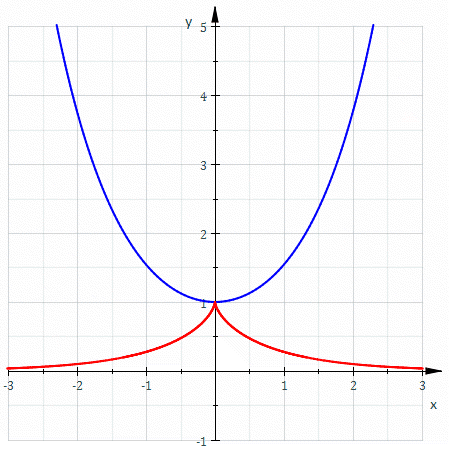
 The parametric representation describes a
The parametric representation describes a
Springerlink
(subscription required). The involute of a circle is also an important shape in gas compressing, as a
Involute
at
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, an involute (also known as an evolvent) is a particular type of curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve.
The evolute
In the differential geometry of curves, the evolute of a curve is the locus (mathematics), locus of all its Center of curvature, centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the result ...
of an involute is the original curve.
It is generalized by the roulette
Roulette (named after the French language, French word meaning "little wheel") is a casino game which was likely developed from the Italy, Italian game Biribi. In the game, a player may choose to place a bet on a single number, various grouping ...
family of curves. That is, the involutes of a curve are the roulettes of the curve generated by a straight line.
The notions of the involute and evolute of a curve were introduced by Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
in his work titled '' Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673), where he showed that the involute of a cycloid is still a cycloid, thus providing a method for constructing the cycloidal pendulum, which has the useful property that its period is independent of the amplitude of oscillation.
Involute of a parameterized curve
Let be a regular curve in the plane with itscurvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
nowhere 0 and , then the curve with the parametric representation
is an ''involute'' of the given curve.
Adding an arbitrary but fixed number to the integral results in an involute corresponding to a string extended by (like a ball of wool yarn
Yarn is a long continuous length of interlocked fibres, used in sewing, crocheting, knitting, weaving, embroidery, ropemaking, and the production of textiles. '' Thread'' is a type of yarn intended for sewing by hand or machine. Modern ...
having some length of thread already hanging before it is unwound). Hence, the involute can be varied by constant and/or adding a number to the integral (see Involutes of a semicubic parabola).
If one gets
:
Properties of involutes
In order to derive properties of a regular curve it is advantageous to suppose thearc length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ...
to be the parameter of the given curve, which lead to the following simplifications: and , with the curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
and the unit normal. One gets for the involute:
: and
:
and the statement:
*At point the involute is ''not regular'' (because ),
and from follows:
* The normal of the involute at point is the tangent of the given curve at point .
* The involutes are parallel curve
A parallel of a curve is the envelope (mathematics), envelope of a family of Congruence (geometry), congruent circles centered on the curve.
It generalises the concept of ''parallel (geometry), parallel (straight) lines''. It can also be defi ...
s, because of and the fact, that is the unit normal at .
The family of involutes and the family of tangents to the original curve makes up an orthogonal coordinate system
In mathematics, orthogonal coordinates are defined as a set of coordinates \mathbf q = (q^1, q^2, \dots, q^d) in which the coordinate hypersurfaces all meet at right angles (note that superscripts are indices, not exponents). A coordinate sur ...
. Consequently, one may construct involutes graphically. First, draw the family of tangent lines. Then, an involute can be constructed by always staying orthogonal to the tangent line passing the point.
Cusps
This section is based on. There are generically two types of cusps in involutes. The first type is at the point where the involute touches the curve itself. This is a cusp of order 3/2. The second type is at the point where the curve has an inflection point. This is a cusp of order 5/2. This can be visually seen by constructing a map defined by where is the arclength parametrization of the curve, and is the slope-angle of the curve at the point . This maps the 2D plane into a surface in 3D space. For example, this maps the circle into thehyperboloid of one sheet
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface (mathematics), surface generated by rotating a hyperbola around one of its Hyperbola#Equation, principal axes. A hyperboloid is the surface obtained ...
.
By this map, the involutes are obtained in a three-step process: map to , then to the surface in , then project it down to by removing the z-axis: where is any real constant.
Since the mapping has nonzero derivative at all , cusps of the involute can only occur where the derivative of is vertical (parallel to the z-axis), which can only occur where the surface in has a vertical tangent plane.
Generically, the surface has vertical tangent planes at only two cases: where the surface touches the curve, and where the curve has an inflection point.
cusp of order 3/2
For the first type, one can start by the involute of a circle, with equationthen set , and expand for small , to obtainthus giving the order 3/2 curve , a semicubical parabola.cusp of order 5/2
Examples
Involutes of a circle
parametric equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters.
In the case ...
of the involute of the circle.
The term is optional; it serves to set the start location of the curve on the circle. The figure shows involutes for (green), (red), (purple) and (light blue). The involutes look like Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
s, but they are actually not.
The arc length for and of the involute is
:
Involutes of a semicubic parabola
Theparametric equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters.
In the case ...
describes a semicubical parabola. From one gets and . Extending the string by extensively simplifies further calculation, and one gets
:
Eliminating yields showing that this involute is a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
.
The other involutes are thus parallel curves of a parabola, and are not parabolas, as they are curves of degree six (See ).

Involutes of a catenary
For thecatenary
In physics and geometry, a catenary ( , ) is the curve that an idealized hanging chain or wire rope, cable assumes under its own weight when supported only at its ends in a uniform gravitational field.
The catenary curve has a U-like shape, ...
, the tangent vector is , and, as its length is . Thus the arc length from the point is
Hence the involute starting from is parametrized by
:
and is thus a tractrix
In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angl ...
.
The other involutes are not tractrices, as they are parallel curves of a tractrix.
Involutes of a cycloid
cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve g ...
. From , one gets (after having used some trigonometric formulas)
:
and
:
Hence the equations of the corresponding involute are
:
:
which describe the shifted red cycloid of the diagram. Hence
* The involutes of the cycloid are parallel curves of the cycloid
:
(Parallel curves of a cycloid are not cycloids.)
Involute and evolute
Theevolute
In the differential geometry of curves, the evolute of a curve is the locus (mathematics), locus of all its Center of curvature, centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the result ...
of a given curve consists of the curvature centers of . Between involutes and evolutes the following statement holds:
:''A curve is the evolute of any of its involutes.''
Application
The most common profiles of moderngear
A gear or gearwheel is a rotating machine part typically used to transmit rotational motion and/or torque by means of a series of teeth that engage with compatible teeth of another gear or other part. The teeth can be integral saliences or ...
teeth are involutes of a circle. In an involute gear
The involute gear profile is the most commonly used system for gearing today, with cycloid gearing still used for some specialties such as clocks. In an involute gear, the profiles of the teeth are ''involutes of a circle.'' The involute of a ...
system, the teeth of two meshing gears contact at a single instantaneous point that follows along a single straight line of action. The forces the contacting teeth exert on each other also follow this line and are normal to the teeth. The involute gear system maintaining these conditions follows the fundamental law of gearing: the ratio of angular velocities between the two gears must remain constant throughout.
With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern planar gear systems are either involute or the related cycloidal gear system.V. G. A. Goss (2013) "Application of analytical geometry to the shape of gear teeth", Resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
18(9): 817 to 3Springerlink
(subscription required). The involute of a circle is also an important shape in gas compressing, as a
scroll compressor
A scroll compressor (also called ''spiral compressor'', scroll pump and scroll vacuum pump) is a device for Compressor, compressing air or refrigerant. It is used in air conditioning equipment, as an automobile supercharger (where it is known ...
can be built based on this shape. Scroll compressors make less sound than conventional compressors and have proven to be quite efficient.
The High Flux Isotope Reactor uses involute-shaped fuel elements, since these allow a constant-width channel between them for coolant.
See also
*Envelope (mathematics)
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of ...
* Evolute
In the differential geometry of curves, the evolute of a curve is the locus (mathematics), locus of all its Center of curvature, centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the result ...
* Goat grazing problem
* Involute gear
The involute gear profile is the most commonly used system for gearing today, with cycloid gearing still used for some specialties such as clocks. In an involute gear, the profiles of the teeth are ''involutes of a circle.'' The involute of a ...
* Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on ...
* Scroll compressor
A scroll compressor (also called ''spiral compressor'', scroll pump and scroll vacuum pump) is a device for Compressor, compressing air or refrigerant. It is used in air conditioning equipment, as an automobile supercharger (where it is known ...
References
External links
Involute
at
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science ...
{{Differential transforms of plane curves
Differential geometry
Roulettes (curve)