Kerr solution on:
[Wikipedia]
[Google]
[Amazon]
The Kerr metric or Kerr geometry describes the geometry of empty
Lecture XXVI: Kerr black holes: I. Metric structure and regularity of particle orbits
p. 1, Eq. 1 where the coordinates are standard
page 485
regarding determinant of metric tensor. Se
page 325
regarding generalizations.
Rotating Black Holes
page 42 :

 There are several important surfaces in the Kerr metric (). The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component ''g'' of the metric goes to infinity. Solving the quadratic equation yields the solution:
:
which in natural units (that give ) simplifies to:
:
While in the Schwarzschild metric the event horizon is also the place where the purely temporal component ''g'' of the metric changes sign from positive to negative, in Kerr metric that happens at a different distance. Again solving a quadratic equation yields the solution:
:
or in natural units:
:
Due to the cos''θ'' term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude ''θ'' equals 0 or ''π''; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component ''g'' is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive
There are several important surfaces in the Kerr metric (). The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component ''g'' of the metric goes to infinity. Solving the quadratic equation yields the solution:
:
which in natural units (that give ) simplifies to:
:
While in the Schwarzschild metric the event horizon is also the place where the purely temporal component ''g'' of the metric changes sign from positive to negative, in Kerr metric that happens at a different distance. Again solving a quadratic equation yields the solution:
:
or in natural units:
:
Due to the cos''θ'' term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude ''θ'' equals 0 or ''π''; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component ''g'' is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive
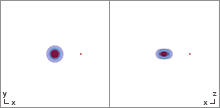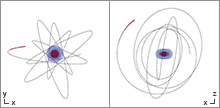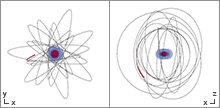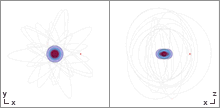 The
The
Gravitation
, pages 899, 900, 908 and Using Hamilton–Jacobi theory,
About Time: Einstein's Unfinished Revolution
/ref> While the physical reality of the anti-universe remains uncertain, its study provides valuable insights into the nature of spacetime, gravity, and the limits of our current understanding of the universe. While it is expected that the exterior region of the Kerr solution is stable, and that all rotating black holes will eventually approach a Kerr metric, the interior region of the solution appears to be unstable, much like a pencil balanced on its point. This is related to the idea of cosmic censorship.
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
around a rotating uncharged axially symmetric black hole
A black hole is a massive, compact astronomical object so dense that its gravity prevents anything from escaping, even light. Albert Einstein's theory of general relativity predicts that a sufficiently compact mass will form a black hole. Th ...
with a quasispherical event horizon
In astrophysics, an event horizon is a boundary beyond which events cannot affect an outside observer. Wolfgang Rindler coined the term in the 1950s.
In 1784, John Michell proposed that gravity can be strong enough in the vicinity of massive c ...
. The Kerr metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
is an exact solution of the Einstein field equations
In the General relativity, general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of Matter#In general relativity and cosmology, matter within it. ...
of general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
; these equations are highly non-linear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
, which makes exact solutions very difficult to find.
Overview
The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered byKarl Schwarzschild
Karl Schwarzschild (; 9 October 1873 – 11 May 1916) was a German physicist and astronomer.
Schwarzschild provided the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-r ...
in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric
In physics and astronomy, the Reissner–Nordström metric is a Static spacetime, static solution to the Einstein–Maxwell equations, Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, s ...
, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black hole physics, with an Afterword by Roy Kerr", Princeton University Press, Princeton, The natural extension to a charged, rotating black hole, the Kerr–Newman metric, was discovered shortly thereafter in 1965. These four related solutions may be summarized by the following table, where ''Q'' represents the body's electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
and ''J'' represents its spin angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
:
:
According to the Kerr metric, a rotating body should exhibit frame-dragging
Frame-dragging is an effect on spacetime, predicted by Albert Einstein's General relativity, general theory of relativity, that is due to non-static stationary distributions of mass–energy. A stationary Field (physics), field is one that is ...
(also known as Lense–Thirring precession
In general relativity, Lense–Thirring precession or the Lense–Thirring effect (; named after Josef Lense and Hans Thirring) is a relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is ...
), a distinctive prediction of general relativity. The first measurement of this frame dragging effect was done in 2011 by the Gravity Probe B
Gravity Probe B (GP-B) was a satellite-based experiment whose objective was to test two previously-unverified predictions of general relativity: the geodetic effect and frame-dragging. This was to be accomplished by measuring, very precisely, t ...
experiment. Roughly speaking, this effect predicts that objects coming close to a rotating mass will be entrained to participate in its rotation, not because of any applied force or torque that can be felt, but rather because of the swirling curvature of spacetime itself associated with rotating bodies. In the case of a rotating black hole, at close enough distances, all objects – even light – ''must'' rotate with the black hole; the region where this holds is called the ergosphere.
The light from distant sources can travel around the event horizon several times (if close enough); creating multiple images of the same object. To a distant viewer, the apparent perpendicular distance between images decreases at a factor of 2 (about 500). However, fast spinning black holes have less distance between multiplicity images.
Rotating black holes have surfaces where the metric seems to have apparent singularities; the size and shape of these surfaces depends on the black hole's mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and angular momentum. The outer surface encloses the ergosphere and has a shape similar to a flattened sphere. The inner surface marks the event horizon; objects passing into the interior of this horizon can never again communicate with the world outside that horizon. However, neither surface is a true singularity, since their apparent singularity can be eliminated in a different coordinate system
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are ...
. A similar situation obtains when considering the Schwarzschild metric which also appears to result in a singularity at dividing the space above and below ''r''s into two disconnected patches; using a different coordinate transformation one can then relate the extended external patch to the inner patch (see ') – such a coordinate transformation eliminates the apparent singularity where the inner and outer surfaces meet. Objects between these two surfaces must co-rotate with the rotating black hole, as noted above; this feature can in principle be used to extract energy from a rotating black hole, up to its invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
energy, ''Mc''2.
The LIGO experiment that first detected gravitational waves, announced in 2016, also provided the first direct observation of a pair of Kerr black holes.
Metric
The Kerr metric is commonly expressed in one of two forms, the Boyer–Lindquist form and the Kerr–Schild form. It can be readily derived from the Schwarzschild metric, using theNewman–Janis algorithm
In general relativity, the Newman–Janis algorithm (NJA) is a complexification technique for finding exact solutions to the Einstein field equations. In 1964, Newman and Janis showed that the Kerr metric could be obtained from the Schwarzschild ...
by Newman–Penrose formalism
The Newman–Penrose (NP) formalism The original paper by Newman and Penrose, which introduces the formalism, and uses it to derive example results.Ezra T Newman, Roger Penrose. ''Errata: An Approach to Gravitational Radiation by a Method of Sp ...
(also known as the spin–coefficient formalism), Ernst equation
In mathematics, the Ernst equation is an integrable non-linear partial differential equation, named after the American physicist .
The Ernst equation
The equation reads:
\Re(u)(u_+u_r/r+u_) = (u_r)^2+(u_z)^2.
where \Re(u) is the real part ...
, or Ellipsoid coordinate transformation.
Boyer–Lindquist coordinates
The Kerr metric describes the geometry of spacetime in the vicinity of a mass rotating with angular momentum . The metric (or equivalently itsline element
In geometry, the line element or length element can be informally thought of as a line segment associated with an infinitesimal displacement vector in a metric space. The length of the line element, which may be thought of as a differential arc ...
for proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. The proper time interval between two events on a world line is the change in proper time ...
) in Boyer–Lindquist coordinates
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.
Th ...
isChristopher M. HirataLecture XXVI: Kerr black holes: I. Metric structure and regularity of particle orbits
p. 1, Eq. 1 where the coordinates are standard
oblate spheroidal coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci ...
, which are equivalent to the cartesian coordinates
where is the Schwarzschild radius
and where for brevity, the length scales and have been introduced as
A key feature to note in the above metric is the cross-term . This implies that there is coupling between time and motion in the plane of rotation that disappears when the black hole's angular momentum goes to zero.
In the non-relativistic limit where (or, equivalently, ) goes to zero, the Kerr metric becomes the orthogonal metric for the oblate spheroidal coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci ...
Kerr–Schild coordinates
The Kerr metric can be expressed in "Kerr–Schild" form, using a particular set ofCartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
as follows. Especially see equations (7.10), (7.11) and (7.14). These solutions were proposed by Kerr
Kerr may refer to:
People
*Kerr (surname)
*Kerr (given name) Places
;United States
*Kerr Township, Champaign County, Illinois
*Kerr, Montana, A US census-designated place
*Kerr, Ohio, an unincorporated community
*Kerr County, Texas
Kerr Co ...
and Schild in 1965.
Notice that k is a unit 3-vector, making the 4-vector a null vector
In mathematics, given a vector space ''X'' with an associated quadratic form ''q'', written , a null vector or isotropic vector is a non-zero element ''x'' of ''X'' for which .
In the theory of real bilinear forms, definite quadratic forms an ...
, with respect to both ''g'' and ''η''. Here ''M'' is the constant mass of the spinning object, ''η'' is the Minkowski tensor, and ''a'' is a constant rotational parameter of the spinning object. It is understood that the vector is directed along the positive z-axis. The quantity ''r'' is not the radius, but rather is implicitly defined by
Notice that the quantity ''r'' becomes the usual radius ''R''
:
when the rotational parameter approaches zero. In this form of solution, units are selected so that the speed of light is unity (). At large distances from the source (''R'' ≫ ''a''), these equations reduce to the Eddington–Finkelstein form of the Schwarzschild metric.
In the Kerr–Schild form of the Kerr metric, the determinant of the metric tensor is everywhere equal to negative one, even near the source.Stephani, Hans et al. ''Exact Solutions of Einstein's Field Equations'' (Cambridge University Press 2003). Sepage 485
regarding determinant of metric tensor. Se
page 325
regarding generalizations.
Soliton coordinates
As the Kerr metric (along with the Kerr–NUT metric) is axially symmetric, it can be cast into a form to which the Belinski–Zakharov transform can be applied. This implies that the Kerr black hole has the form of a gravitational soliton.Mass of rotational energy
If the complete rotational energy of a black hole is extracted, for example with the Penrose process, the remaining mass cannot shrink below the irreducible mass. Therefore, if a black hole rotates with the spin , its total mass-equivalent is higher by a factor of in comparison with a corresponding Schwarzschild black hole where is equal to . The reason for this is that in order to get a static body to spin, energy needs to be applied to the system. Because of themass–energy equivalence
In physics, mass–energy equivalence is the relationship between mass and energy in a system's rest frame. The two differ only by a multiplicative constant and the units of measurement. The principle is described by the physicist Albert Einstei ...
this energy also has a mass-equivalent, which adds to the total mass–energy of the system, .
The total mass equivalent (the gravitating mass) of the body (including its rotational energy
Rotational energy or angular kinetic energy is kinetic energy due to the rotation of an object and is part of its total kinetic energy. Looking at rotational energy separately around an object's axis of rotation, the following dependence on the ob ...
) and its irreducible mass are related byStijn van TongerenRotating Black Holes
page 42 :
Wave operator
Since even a direct check on the Kerr metric involves cumbersome calculations, the contravariant components of themetric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
in Boyer–Lindquist coordinates are shown below in the expression for the square of the four-gradient
In differential geometry, the four-gradient (or 4-gradient) \boldsymbol is the four-vector analogue of the gradient \vec from vector calculus.
In special relativity and in quantum mechanics, the four-gradient is used to define the properties and ...
operator:
Frame dragging
We may rewrite the Kerr metric () in the following form: This metric is equivalent to a co-rotating reference frame that is rotating with angular speed Ω that depends on both the radius ''r'' and thecolatitude
In a spherical coordinate system, a colatitude is the complementary angle of a given latitude, i.e. the difference between a right angle and the latitude. In geography, Southern latitudes are defined to be negative, and as a result the colatitude ...
''θ'', where Ω is called the Killing horizon.
Thus, an inertial reference frame is entrained by the rotating central mass to participate in the latter's rotation; this is called frame-dragging, and has been tested experimentally.
Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction. An "ice skater", in orbit over the equator and rotationally at rest with respect to the stars, extends her arms. The arm extended toward the black hole will be torqued spinward. The arm extended away from the black hole will be torqued anti-spinward. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This is the opposite of what happens in everyday experience. If she is already rotating at a certain speed when she extends her arms, inertial effects and frame-dragging effects will balance and her spin will not change. Due to the equivalence principle
The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same t ...
, gravitational effects are locally indistinguishable from inertial effects, so this rotation rate, at which when she extends her arms nothing happens, is her local reference for non-rotation. This frame is rotating with respect to the fixed stars and counter-rotating with respect to the black hole. A useful metaphor is a planetary gear
An epicyclic gear train (also known as a planetary gearset) is a Reduction drive, gear reduction assembly consisting of two gears mounted so that the center of one gear (the "planet") revolves around the center of the other (the "sun"). A carri ...
system with the black hole being the sun gear, the ice skater being a planetary gear and the outside universe being the ring gear. This can also be interpreted through Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle (or Mach's conjecture) is the name given by Albert Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach. The ...
.
Important surfaces
 There are several important surfaces in the Kerr metric (). The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component ''g'' of the metric goes to infinity. Solving the quadratic equation yields the solution:
:
which in natural units (that give ) simplifies to:
:
While in the Schwarzschild metric the event horizon is also the place where the purely temporal component ''g'' of the metric changes sign from positive to negative, in Kerr metric that happens at a different distance. Again solving a quadratic equation yields the solution:
:
or in natural units:
:
Due to the cos''θ'' term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude ''θ'' equals 0 or ''π''; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component ''g'' is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive
There are several important surfaces in the Kerr metric (). The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component ''g'' of the metric goes to infinity. Solving the quadratic equation yields the solution:
:
which in natural units (that give ) simplifies to:
:
While in the Schwarzschild metric the event horizon is also the place where the purely temporal component ''g'' of the metric changes sign from positive to negative, in Kerr metric that happens at a different distance. Again solving a quadratic equation yields the solution:
:
or in natural units:
:
Due to the cos''θ'' term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude ''θ'' equals 0 or ''π''; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component ''g'' is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. The proper time interval between two events on a world line is the change in proper time ...
along its worldline, its path through spacetime. However, this is impossible within the ergosphere, where ''g'' is negative, unless the particle is co-rotating around the interior mass with an angular speed at least of . Thus, no particle can move in the direction opposite to central mass's rotation within the ergosphere.
As with the event horizon in the Schwarzschild metric, the apparent singularity at ''r'' is due to the choice of coordinates (i.e., it is a coordinate singularity
In mathematics and physics, a coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame that can be removed by choosing a different frame.
An example is the apparent (longitudinal) singularity a ...
). In fact, the spacetime can be smoothly continued through it by an appropriate choice of coordinates. In turn, the outer boundary of the ergosphere at ''r'' is not singular by itself even in Kerr coordinates due to non-zero term.
Ergosphere and the Penrose process
A black hole in general is surrounded by a surface, called the event horizon and situated at the Schwarzschild radius for a nonrotating black hole, where the escape velocity is equal to the velocity of light. Within this surface, no observer/particle can maintain itself at a constant radius. It is forced to fall inwards, and so this is sometimes called the ''static limit''. A rotating black hole has the same static limit at its event horizon but there is an additional surface outside the event horizon named the "ergosurface" given by : inBoyer–Lindquist coordinates
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.
Th ...
, which can be intuitively characterized as the sphere where "the rotational velocity of the surrounding space" is dragged along with the velocity of light. Within this sphere the dragging is greater than the speed of light, and any observer/particle is forced to co-rotate.
The region outside the event horizon but inside the surface where the rotational velocity is the speed of light, is called the ''ergosphere'' (from Greek ''ergon'' meaning ''work''). Particles falling within the ergosphere are forced to rotate faster and thereby gain energy. Because they are still outside the event horizon, they may escape the black hole. The net process is that the rotating black hole emits energetic particles at the cost of its own total energy. The possibility of extracting spin energy from a rotating black hole was first proposed by the mathematician Roger Penrose
Sir Roger Penrose (born 8 August 1931) is an English mathematician, mathematical physicist, Philosophy of science, philosopher of science and Nobel Prize in Physics, Nobel Laureate in Physics. He is Emeritus Rouse Ball Professor of Mathematics i ...
in 1969 and is thus called the Penrose process. Rotating black holes in astrophysics are a potential source of large amounts of energy and are used to explain energetic phenomena, such as gamma-ray burst
In gamma-ray astronomy, gamma-ray bursts (GRBs) are extremely energetic events occurring in distant Galaxy, galaxies which represent the brightest and most powerful class of explosion in the universe. These extreme Electromagnetic radiation, ele ...
s.
Features
The Kerr geometry exhibits many noteworthy features: the maximal analytic extension includes a sequence of asymptotically flat exterior regions, each associated with an ergosphere, stationary limit surfaces,event horizon
In astrophysics, an event horizon is a boundary beyond which events cannot affect an outside observer. Wolfgang Rindler coined the term in the 1950s.
In 1784, John Michell proposed that gravity can be strong enough in the vicinity of massive c ...
s, Cauchy horizons, closed timelike curve
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van St ...
s, and a ring-shaped curvature singularity. The geodesic equation
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
can be solved exactly in closed form. In addition to two Killing vector fields
In mathematics, a Killing vector field (often called a Killing field), named after Wilhelm Killing, is a vector field on a pseudo-Riemannian manifold that preserves the metric tensor. Killing vector fields are the Lie group#The Lie algebra associa ...
(corresponding to ''time translation
Time-translation symmetry or temporal translation symmetry (TTS) is a mathematical transformation in physics that moves the times of events through a common interval. Time-translation symmetry is the law that the laws of physics are unchanged ...
'' and ''axisymmetry''), the Kerr geometry admits a remarkable Killing tensor In mathematics, a Killing tensor or Killing tensor field is a generalization of a Killing vector, for symmetric tensor fields instead of just vector fields. It is a concept in Riemannian and pseudo-Riemannian geometry, and is mainly used in th ...
. There is a pair of principal null congruences (one ''ingoing'' and one ''outgoing''). The Weyl tensor is algebraically special, in fact it has Petrov type D. The global structure is known. Topologically, the homotopy type
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A ...
of the Kerr spacetime can be simply characterized as a line with circles attached at each integer point.
Note that the inner Kerr geometry is unstable with regard to perturbations in the interior region. This instability means that although the Kerr metric is axis-symmetric, a black hole created through gravitational collapse may not be so. This instability also implies that many of the features of the Kerr geometry described above may not be present inside such a black hole.
A surface on which light can orbit a black hole is called a photon sphere. The Kerr solution has infinitely many photon sphere
A photon sphere, or photon ring or photon circle, arises in a neighbourhood of the event horizon of a black hole where gravity is so strong that emitted photons will not just bend around the black hole but also return to the point where they we ...
s, lying between an inner one and an outer one. In the nonrotating, Schwarzschild solution, with , the inner and outer photon spheres degenerate, so that there is only one photon sphere at a single radius. The greater the spin of a black hole, the farther from each other the inner and outer photon spheres move. A beam of light traveling in a direction opposite to the spin of the black hole will circularly orbit the hole at the outer photon sphere. A beam of light traveling in the same direction as the black hole's spin will circularly orbit at the inner photon sphere. Orbiting geodesics with some angular momentum perpendicular to the axis of rotation of the black hole will orbit on photon spheres between these two extremes. Because the spacetime is rotating, such orbits exhibit a precession, since there is a shift in the variable after completing one period in the variable.
Trajectory equations
 The
The equations of motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathem ...
for test particle In physical theories, a test particle, or test charge, is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insuf ...
s in the Kerr spacetime are governed by four constants of motion In mechanics, a constant of motion is a physical quantity conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather tha ...
. The first is the invariant mass of the test particle, defined by the relation
where is the four-momentum
In special relativity, four-momentum (also called momentum–energy or momenergy) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum i ...
of the particle. Furthermore, there are two constants of motion given by the time translation and rotation symmetries of Kerr spacetime, the energy , and the component of the orbital angular momentum parallel to the spin of the black hole .Misner, Thorne & WheelerGravitation
, pages 899, 900, 908 and Using Hamilton–Jacobi theory,
Brandon Carter
Brandon Carter, (born 1942) is an Australian theoretical physics, theoretical physicist who explores the properties of black holes, and was the first to name and employ the anthropic principle in its contemporary form. He is a researcher at t ...
showed that there exists a fourth constant of motion, , now referred to as the Carter constant. It is related to the total angular momentum of the particle and is given by
Since there are four (independent) constants of motion for degrees of freedom, the equations of motion for a test particle in Kerr spacetime are integrable.
Using these constants of motion, the trajectory equations for a test particle can be written (using natural units of ),
with
*
*
*
where is an affine parameter such that . In particular, when the affine parameter , is related to the proper time through .
Because of the frame-dragging
Frame-dragging is an effect on spacetime, predicted by Albert Einstein's General relativity, general theory of relativity, that is due to non-static stationary distributions of mass–energy. A stationary Field (physics), field is one that is ...
-effect, a zero-angular-momentum observer (ZAMO) is corotating with the angular velocity which is defined with respect to the bookkeeper's coordinate time . The local velocity of the test-particle is measured relative to a probe corotating with . The gravitational time-dilation between a ZAMO at fixed and a stationary observer far away from the mass is
In Cartesian Kerr–Schild coordinates, the equations for a photon are
where is analogous to Carter's constant and is a useful quantity
If we set , the Schwarzschild geodesics
In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass M, that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the tests of gener ...
are restored.
Symmetries
The group of isometries of the Kerr metric is the subgroup of the ten-dimensionalPoincaré group
The Poincaré group, named after Henri Poincaré (1905), was first defined by Hermann Minkowski (1908) as the isometry group of Minkowski spacetime. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our unde ...
which takes the two-dimensional locus of the singularity to itself. It retains the time translation
Time-translation symmetry or temporal translation symmetry (TTS) is a mathematical transformation in physics that moves the times of events through a common interval. Time-translation symmetry is the law that the laws of physics are unchanged ...
s (one dimension) and rotations around its axis of rotation (one dimension). Thus it has two dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the component which reverses time and longitude; the component which reflects through the equatorial plane; and the component that does both.
In physics, symmetries are typically associated with conserved constants of motion, in accordance with Noether's theorem
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems (see Noether's second theorem) published by the mat ...
. As shown above, the geodesic equations have four conserved quantities: one of which comes from the definition of a geodesic, and two of which arise from the time translation and rotation symmetry of the Kerr geometry. The fourth conserved quantity does not arise from a symmetry in the standard sense and is commonly referred to as a hidden symmetry.
Overextreme Kerr solutions
The location of the event horizon is determined by the larger root of . When (i.e. ), there are no (real valued) solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a naked singularity.Kerr black holes as wormholes
Although the Kerr solution appears to be singular at the roots of , these are actually coordinate singularities, and, with an appropriate choice of new coordinates, the Kerr solution can be smoothly extended through the values of corresponding to these roots. The larger of these roots determines the location of the event horizon, and the smaller determines the location of a Cauchy horizon. A (future-directed, time-like) curve can start in the exterior and pass through the event horizon. Once having passed through the event horizon, the coordinate now behaves like a time coordinate, so it must decrease until the curve passes through the Cauchy horizon.Anti-universe region
The Kerr metric, which describes the spacetime geometry around a rotating black hole, can be extended beyond the inner event horizon. In the Boyer-Lindquist coordinate system , this inner horizon is located at As one crosses this inner horizon, the radial coordinate continues to decrease, even becoming negative.The ring singularity and beyond
At , a peculiar feature arises: a ring singularity. Unlike the point singularity in the Schwarzschild metric (a non-rotating black hole), the Kerr singularity is not a single point but a ring lying in the equatorial plane (). This ring singularity acts as a portal to a new region of spacetime. If we avoid the equatorial plane (), we can smoothly continue the coordinate to negative values. This region with is interpreted as an entirely new, asymptotically flat universe, often called the "anti-universe." This anti-universe has some surprising properties: Negative ADM Mass: The anti-universe possesses a negative Arnowitt-Deser-Misner (ADM) mass, which can be thought of as the total mass-energy of the spacetime as measured at infinity. A negative mass is a highly unusual concept in general relativity, and its physical interpretation is still debated.Closed timelike curves and the Cauchy horizon
Within the anti-universe, an even stranger phenomenon occurs. The metric component , which is related to the azimuthal direction around the ring singularity, can change sign. Specifically, is given by: When becomes negative, the coordinate becomes timelike, and a linear combination of the coordinates and becomes spacelike. This leads to the existence of closed timelike curves (CTCs). A CTC is a path through spacetime where an object could travel back to its own past, violating causality. The boundary where changes sign and CTCs first appear is called the Cauchy horizon. It is defined by the condition , which gives The Cauchy horizon acts as a boundary beyond which the familiar notions of cause and effect break down. The presence of CTCs raises fundamental questions about the predictability and consistency of the laws of physics in these extreme regions of spacetime. The anti-universe region of the extended Kerr metric is a fascinating and perplexing theoretical construct. It presents a scenario with a negative mass, reversed time orientation, and the possibility of time travel through closed timelike curves.Paul Davies
Paul Charles William Davies (born 22 April 1946) is an English physicist, writer and broadcaster, a professor in Arizona State University and director of BEYOND: Center for Fundamental Concepts in Science. He is affiliated with the Institute ...
About Time: Einstein's Unfinished Revolution
/ref> While the physical reality of the anti-universe remains uncertain, its study provides valuable insights into the nature of spacetime, gravity, and the limits of our current understanding of the universe. While it is expected that the exterior region of the Kerr solution is stable, and that all rotating black holes will eventually approach a Kerr metric, the interior region of the solution appears to be unstable, much like a pencil balanced on its point. This is related to the idea of cosmic censorship.
Relation to other exact solutions
The Kerr geometry is a particular example of a stationary axially symmetricvacuum solution
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress–energy tensor also vanishes identically, so that no matter or n ...
to the Einstein field equation
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Albert Einstein in 1915 in the ...
. The family of all stationary axially symmetric vacuum solutions to the Einstein field equation are the Ernst vacuums.
The Kerr solution is also related to various non-vacuum solutions which model black holes. For example, the Kerr–Newman electrovacuum models a (rotating) black hole endowed with an electric charge, while the Kerr–Vaidya null dust models a (rotating) hole with infalling electromagnetic radiation.
The special case of the Kerr metric yields the Schwarzschild metric, which models a ''nonrotating'' black hole which is static and spherically symmetric, in the Schwarzschild coordinates. (In this case, every Geroch moment but the mass vanishes.)
The ''interior'' of the Kerr geometry, or rather a portion of it, is locally isometric to the Chandrasekhar–Ferrari CPW vacuum, an example of a colliding plane wave
In physics, a collision is any event in which two or more bodies exert forces on each other in a relatively short time. Although the most common use of the word ''collision'' refers to incidents in which two or more objects collide with great for ...
model. This is particularly interesting, because the global structure of this CPW solution is quite different from that of the Kerr geometry, and in principle, an experimenter could hope to study the geometry of (the outer portion of) the Kerr interior by arranging the collision of two suitable gravitational plane waves.
Multipole moments
Each asymptotically flat Ernst vacuum can be characterized by giving the infinite sequence of relativisticmultipole moment
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Multipol ...
s, the first two of which can be interpreted as the mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
of the source of the field. There are alternative formulations of relativistic multipole moments due to Hansen, Thorne, and Geroch, which turn out to agree with each other. The relativistic multipole moments of the Kerr geometry were computed by Hansen; they turn out to be
:
Thus, the special case of the Schwarzschild vacuum
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumpti ...
() gives the "monopole point source
A point source is a single identifiable ''localized'' source of something. A point source has a negligible extent, distinguishing it from other source geometries. Sources are called point sources because, in mathematical modeling, these sources ...
" of general relativity.''Warning:'' Do not confuse the relativistic multipole moments computed by Hansen with the Weyl multipole moments discussed below.
''Weyl multipole moments'' arise from treating a certain metric function (formally corresponding to Newtonian gravitational potential) which appears the Weyl–Papapetrou chart for the Ernst family of all stationary axisymmetric vacuum solutions using the standard euclidean scalar multipole moment
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Multipol ...
s. They are distinct from the moments computed by Hansen, above. In a sense, the Weyl moments only (indirectly) characterize the "mass distribution" of an isolated source, and they turn out to depend only on the ''even order'' relativistic moments. In the case of solutions symmetric across the equatorial plane the ''odd order'' Weyl moments vanish. For the Kerr vacuum solutions, the first few Weyl moments are given by
:
In particular, we see that the Schwarzschild vacuum has nonzero second order Weyl moment, corresponding to the fact that the "Weyl monopole" is the Chazy–Curzon vacuum solution, not the Schwarzschild vacuum solution, which arises from the Newtonian potential of a certain finite length uniform density thin ''rod''.
In weak field general relativity, it is convenient to treat isolated sources using another type of multipole, which generalize the Weyl moments to ''mass multipole moments'' and ''momentum multipole moments'', characterizing respectively the distribution of mass and of momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
of the source. These are multi-indexed quantities whose suitably symmetrized and anti-symmetrized parts can be related to the real and imaginary parts of the relativistic moments for the full nonlinear theory in a rather complicated manner.
Perez and Moreschi have given an alternative notion of "monopole solutions" by expanding the standard NP tetrad of the Ernst vacuums in powers of (the radial coordinate in the Weyl–Papapetrou chart). According to this formulation:
* the isolated mass monopole source with ''zero'' angular momentum is the ''Schwarzschild vacuum'' family (one parameter),
* the isolated mass monopole source with ''radial'' angular momentum is the '' Taub–NUT vacuum'' family (two parameters; not quite asymptotically flat),
* the isolated mass monopole source with ''axial'' angular momentum is the ''Kerr vacuum'' family (two parameters).
In this sense, the Kerr vacuums are the simplest stationary axisymmetric asymptotically flat vacuum solutions in general relativity.
Open problems
The Kerr geometry is often used as a model of arotating black hole
A rotating black hole is a black hole that possesses angular momentum. In particular, it rotates about one of its axes of symmetry.
All currently known celestial objects, including planets, stars (Sun), galaxies, and black holes, spin about one ...
but if the solution is held to be valid only outside some compact region (subject to certain restrictions), in principle, it should be able to be used as an exterior solution to model the gravitational field around a rotating massive object other than a black hole such as a neutron star
A neutron star is the gravitationally collapsed Stellar core, core of a massive supergiant star. It results from the supernova explosion of a stellar evolution#Massive star, massive star—combined with gravitational collapse—that compresses ...
, or the Earth. This works out very nicely for the non-rotating case, where the Schwarzschild vacuum exterior can be matched to a Schwarzschild fluid interior, and indeed to more general static spherically symmetric perfect fluid solutions. However, the problem of finding a rotating perfect-fluid interior which can be matched to a Kerr exterior, or indeed to any asymptotically flat vacuum exterior solution, has proven very difficult. In particular, the Wahlquist fluid, which was once thought to be a candidate for matching to a Kerr exterior, is now known not to admit any such matching. At present, it seems that only approximate solutions modeling slowly rotating fluid balls are known (These are the relativistic analog of oblate spheroidal balls with nonzero mass and angular momentum but vanishing higher multipole moments). However, the exterior of the Neugebauer–Meinel disk, an exact dust solution
In general relativity, a dust solution is a fluid solution, a type of exact solution of the Einstein field equation, in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid that has ' ...
which models a rotating thin disk, approaches in a limiting case the Kerr geometry. Physical thin-disk solutions obtained by identifying parts of the Kerr spacetime are also known.
See also
*Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumpti ...
* De Sitter-Schwarzschild metric
* Kerr–Newman metric
* Kerr–Newman–de–Sitter metric
* Reissner–Nordström metric
In physics and astronomy, the Reissner–Nordström metric is a Static spacetime, static solution to the Einstein–Maxwell equations, Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, s ...
* Hartle–Thorne metric
* Spin-flip
* Rotating black hole
A rotating black hole is a black hole that possesses angular momentum. In particular, it rotates about one of its axes of symmetry.
All currently known celestial objects, including planets, stars (Sun), galaxies, and black holes, spin about one ...
Footnotes
References
Further reading
* * * * * ''See chapter 19'' for a readable introduction at the advanced undergraduate level. * ''See chapters 6--10'' for a very thorough study at the advanced graduate level. * ''See chapter 13'' for the Chandrasekhar/Ferrari CPW model. * ''See chapter 7''. * * Characterization of three standard families of vacuum solutions as noted above. * Gives the relativistic multipole moments for the Ernst vacuums (plus the electromagnetic and gravitational relativistic multipole moments for the charged generalization). * * * * "... This note is meant to be a guide for those readers who wish to verify all the details f the derivation of the Kerr solution..." {{DEFAULTSORT:Kerr Metric Exact solutions in general relativity Black holes Metric tensors Gravitational singularities fr:Trou noir de Kerr#Métrique de Kerr