|
Static Spherically Symmetric Perfect Fluid
In metric theories of gravitation, particularly general relativity, a static spherically symmetric perfect fluid solution (a term which is often abbreviated as ssspf) is a spacetime equipped with suitable tensor fields which models a static round ball of a fluid with isotropic pressure. Such solutions are often used as idealized models of stars, especially compact objects such as white dwarfs and especially neutron stars. In general relativity, a model of an ''isolated'' star (or other fluid ball) generally consists of a fluid-filled interior region, which is technically a perfect fluid solution of the Einstein field equation, and an exterior region, which is an asymptotically flat vacuum solution. These two pieces must be carefully ''matched'' across the ''world sheet'' of a spherical surface, the ''surface of zero pressure''. (There are various mathematical criteria called matching conditions for checking that the required matching has been successfully achieved.) Similar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Theories Of Gravitation
Metric or metrical may refer to: * Metric system, an internationally adopted decimal system of measurement * An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement Mathematics In mathematics, metric may refer to one of two related, but distinct concepts: * A function which measures distance between two points in a metric space * A metric tensor, in differential geometry, which allows defining lengths of curves, angles, and distances in a manifold Natural sciences * Metric tensor (general relativity), the fundamental object of study in general relativity, similar to the gravitational field in Newtonian physics * Senses related to measurement: ** Metric system, an internationally adopted decimal system of measurement ** Metric units, units related to a metric system ** International System of Units, or ''Système International'' (SI), the most widely used metric system * METRIC, a model that uses Landsat satellite data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotically Flat
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime. While this notion makes sense for any Lorentzian manifold, it is most often applied to a spacetime standing as a solution to the field equations of some metric theory of gravitation, particularly general relativity. In this case, we can say that an asymptotically flat spacetime is one in which the gravitational field, as well as any matter or other fields which may be present, become negligible in magnitude at large distances from some region. In particular, in an asymptotically flat vacuum solution, the gravitational field (curvature) becomes negligible at large distances from the source of the field (typically some isolated massive object such as a star). Intuitive significance The condition of asymptotic flatness is analogous to sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of ''nested round spheres''. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is ''adapted'' to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented. These charts have many applications in metric theories of gravitation such as general relativity. They are most often used in static spherically symmetric spacetimes. In the case of general relativity, Birkhoff's theorem states that every ''isolated'' spherically symmetric vacuum or electrovacuum solution of the Einstein field equation is static, but this is certa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic Coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of ''nested round spheres''. There are several different types of coordinate chart which are ''adapted'' to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often useful. The defining characteristic of an isotropic chart is that its radial coordinate (which is different from the radial coordinate of a Schwarzschild chart) is defined so that light cones appear ''round''. This means that (except in the trivial case of a locally flat manifold), the angular isotropic coordinates do not faithfully represent distances within the nested spheres, nor does the radial coordinate faithfully represent radial distances. On the other hand, angles in the constant time hyperslices are represented without distortion, hence the name of the chart. Isotropic charts are most often applied to static spherically symmetric spacetimes in metric theories of gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
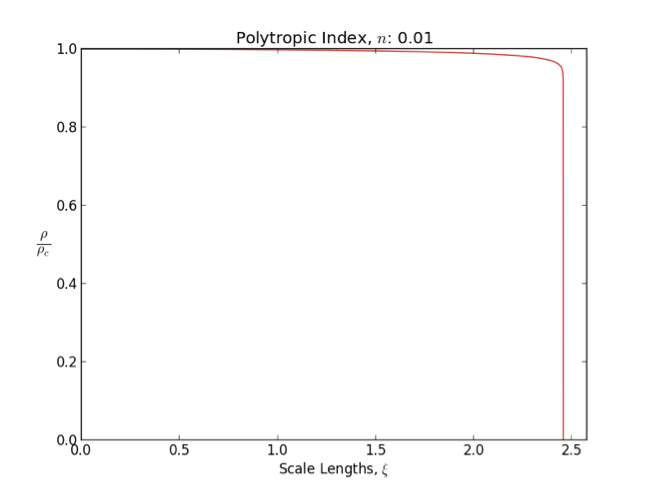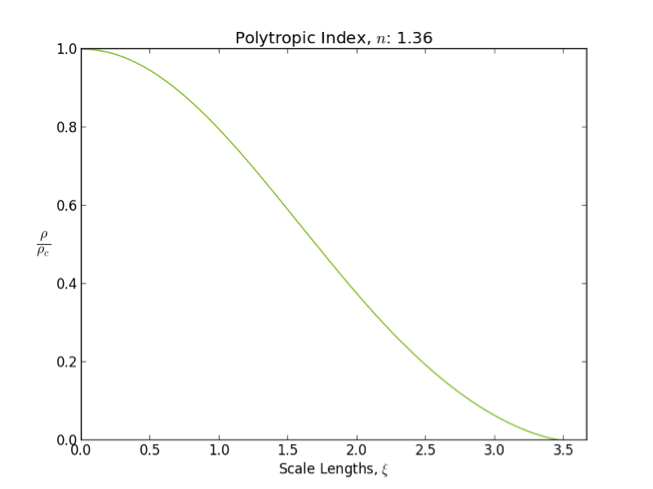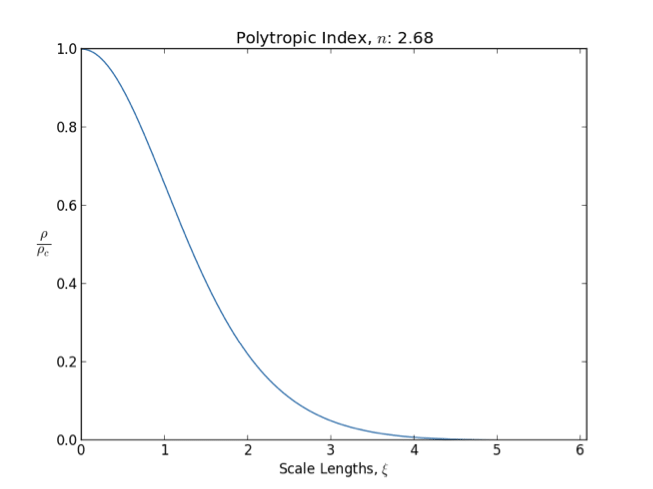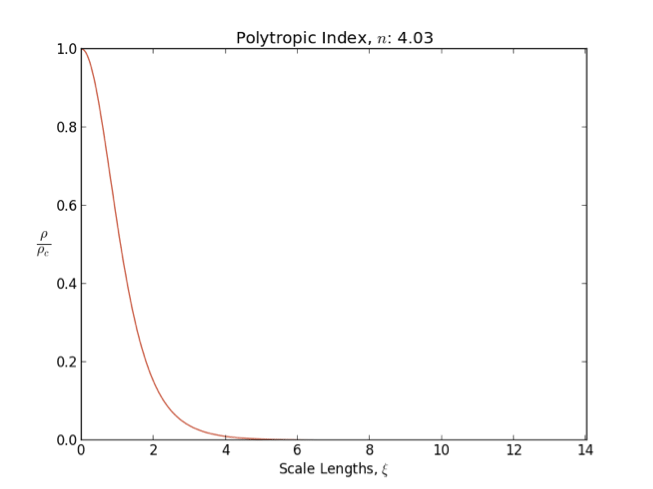
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form :P = K \rho^, where is pressure, is density and is a constant of proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer to an equation of state that looks similar to the thermody ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrostatic Equilibrium
In fluid mechanics, hydrostatic equilibrium (hydrostatic balance, hydrostasy) is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. Hydrostatic equilibrium is the distinguishing criterion between dwarf planets and small solar system bodies, and features in astrophysics and planetary geology. Said qualification of equilibrium indicates that the shape of the object is symmetrically ellipsoid, where any irregular surface features are consequent to a relatively thin solid crust. In addition to the Sun, there are a dozen or so equilibrium objects confirmed to exist in the Solar System. Mathematical consideration For a hydrostatic fluid o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior Schwarzschild Metric
In Einstein's theory of general relativity, the interior Schwarzschild metric (also interior Schwarzschild solution or Schwarzschild fluid solution) is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid (implying that density is constant throughout the body) and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric. Mathematics The interior Schwarzschild metric is framed in a spherical coordinate system with the body's centre located at the origin, plus the time coordinate. Its line element is : c^2 ^ = -\frac \left( 3 \sqrt-\sqrt \right)^2 c^2 dt^2 + \left( 1-\frac \right)^ dr^2 + r^2 \left(d\theta^2 + \sin^2\theta \, d\varphi^2\right), where * \tau is the proper time (time measured by a clock moving along the same world line with the test p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matching Conditions
Matching may refer to: * Matching, Essex, England ** Matching Green ** Matching Tye * Matching (graph theory), in graph theory, a set of edges without common vertices * Graph matching, detection of similarity between graphs * Matching (statistics), a technique for reducing bias when analyzing data from observational studies * Matching funds, funds set to be paid in equal amount to funds available from other sources * Matching principle, an accounting method * Matching theory (economics), the assigning of job candidates to vacancies * Matching law, in behaviorism and learning, the matching law suggests that an animal's response rate to a scenario will be proportionate to the amount/duration of reinforcement delivered * National Resident Matching Program, the process of allocating medical graduates to internship programs * Matchmaking, the process of introducing people for the purpose of marriage * Impedance matching, in electronics, attempting to make the output impedance of a sour ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |