astrophysics Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline, James Keeler, said, astrophysics "seeks to ascertain the ...

, a polytrope refers to a solution of the

Lane–Emden equation In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson's equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer L ...

in which the

pressure Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...

depends upon the

density Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...

in the form

P = K \rho^ = K \rho^,

where is pressure, is density and is a constant of proportionality. The constant is known as the polytropic index; note however that the

polytropic index A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and com ...

has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an

equation of state In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most mo ...

, which states ''P'' as a function of both ρ and ''T'' (the

temperature Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...

); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with

radius In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...

in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer to an equation of state that looks similar to the

thermodynamic Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of th ...

relation above, although this is potentially confusing and is to be avoided. It is preferable to refer to the

fluid In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...

itself (as opposed to the solution of the Lane–Emden equation) as a polytropic fluid or polytropic gas. Specifically, the polytropic gas is a gas for which the

specific heat In thermodynamics, the specific heat capacity (symbol ) of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat ...

is constant. The equation of state of a polytropic fluid is general enough that such idealized fluids find wide use outside of the limited problem of polytropes. The polytropic exponent (of a polytrope) has been shown to be equivalent to the pressure

derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...

of the

bulk modulus The bulk modulus (K or B or k) of a substance is a measure of the resistance of a substance to bulk compression. It is defined as the ratio of the infinitesimal pressure increase to the resulting ''relative'' decrease of the volume. Other mo ...

Weppner, S. P., McKelvey, J. P., Thielen, K. D. and Zielinski, A. K., "A variable polytrope index applied to planet and material models",

Monthly Notices of the Royal Astronomical Society ''Monthly Notices of the Royal Astronomical Society'' (MNRAS) is a peer-reviewed scientific journal in astronomy, astrophysics and related fields. It publishes original research in two formats: papers (of any length) and letters (limited to ...

, Vol. 452, No. 2 (Sept. 2015), pages 1375–1393, Oxford University Press also found a
the arXiv
/ref> where its relation to the

Murnaghan equation of state The Murnaghan equation of state is a relationship between the volume of a body and the pressure to which it is subjected. This is one of many state equations that have been used in earth sciences and shock physics to model the behavior of matter u ...

has also been demonstrated. The polytrope relation is therefore best suited for relatively low-pressure (below 10⁷ Pa) and high-pressure (over 10¹⁴ Pa) conditions when the pressure derivative of the bulk modulus, which is equivalent to the polytrope index, is near constant.

Example models by polytropic index

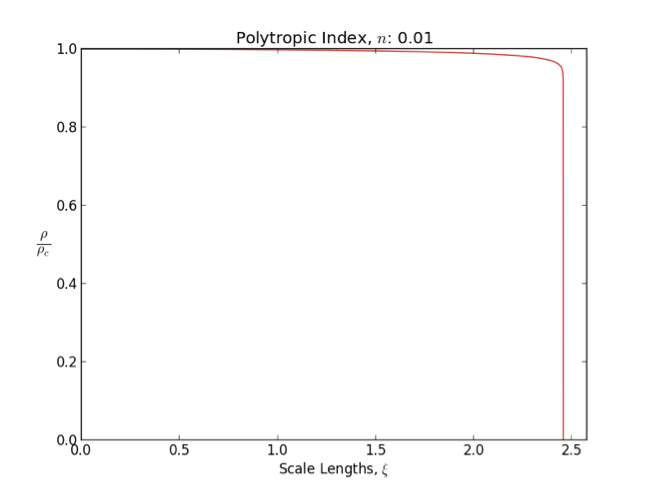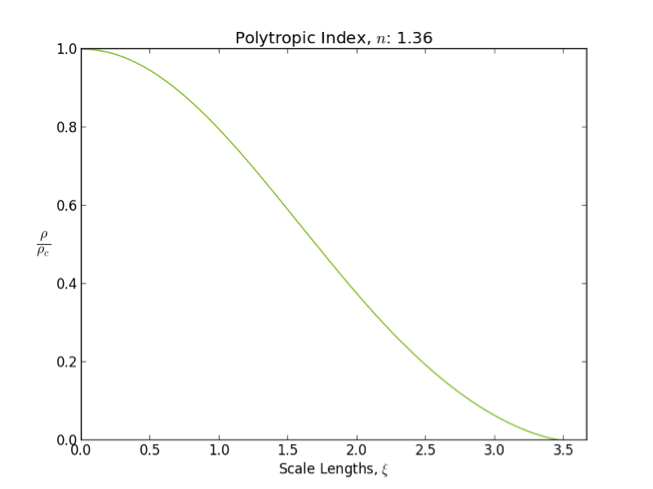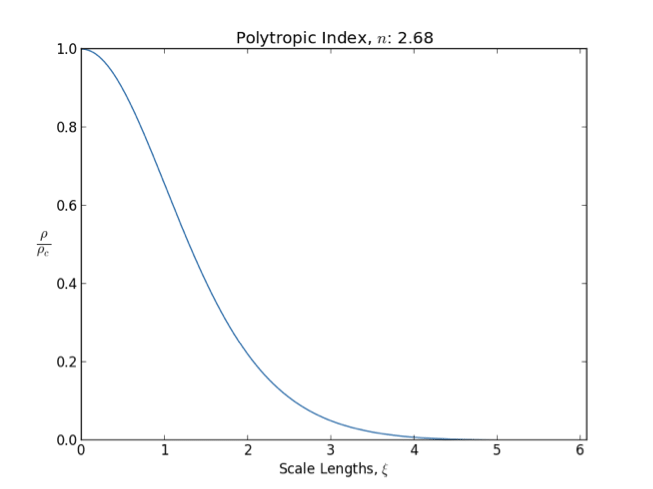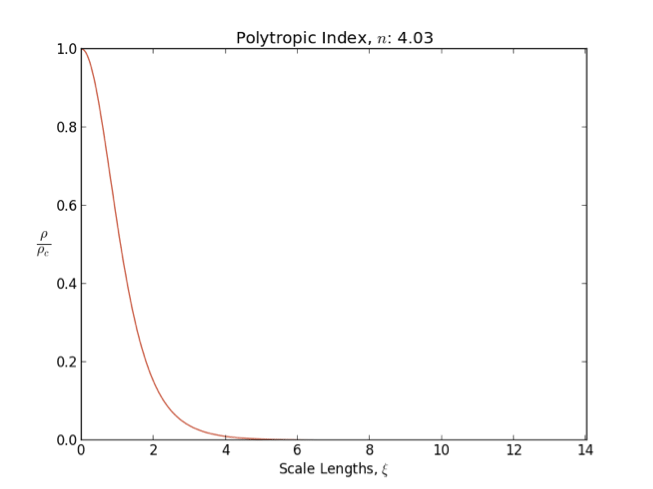
*An index polytrope is often used to model

rocky planet A terrestrial planet, tellurian planet, telluric planet, or rocky planet, is a planet that is composed primarily of silicate, rocks or metals. Within the Solar System, the terrestrial planets accepted by the IAU are the inner planets closest to ...

s. The reason is that polytrope has constant density, i.e., incompressible interior. This is a zero order approximation for rocky (solid/liquid) planets. *

Neutron star A neutron star is the gravitationally collapsed Stellar core, core of a massive supergiant star. It results from the supernova explosion of a stellar evolution#Massive star, massive star—combined with gravitational collapse—that compresses ...

s are well modeled by polytropes with index between and . *A polytrope with index is a good model for fully convective star cores (like those of

red giant A red giant is a luminous giant star of low or intermediate mass (roughly 0.3–8 solar masses ()) in a late phase of stellar evolution. The stellar atmosphere, outer atmosphere is inflated and tenuous, making the radius large and the surface t ...

s),

brown dwarf Brown dwarfs are substellar objects that have more mass than the biggest gas giant planets, but less than the least massive main sequence, main-sequence stars. Their mass is approximately 13 to 80 Jupiter mass, times that of Jupiter ()not big en ...

s, giant gaseous planets (like

Jupiter Jupiter is the fifth planet from the Sun and the List of Solar System objects by size, largest in the Solar System. It is a gas giant with a Jupiter mass, mass more than 2.5 times that of all the other planets in the Solar System combined a ...

). With this index, the polytropic exponent is 5/3, which is the

heat capacity ratio In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant vol ...

(γ) for

monatomic gas In physics and chemistry, "monatomic" is a combination of the words "mono" and "atomic", and means "single atom". It is usually applied to gases: a monatomic gas is a gas in which atoms are not bound to each other. Examples at standard conditions ...

. For the interior of gaseous stars (consisting of either

ionized Ionization or ionisation is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule i ...

hydrogen Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...

helium Helium (from ) is a chemical element; it has chemical symbol, symbol He and atomic number 2. It is a colorless, odorless, non-toxic, inert gas, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling point is ...

), this follows from an

ideal gas An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...

approximation for

natural convection Convection is single or multiphase fluid flow that occurs spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the conve ...

conditions. *A polytrope with index is also a good model for

white dwarf A white dwarf is a Compact star, stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very density, dense: in an Earth sized volume, it packs a mass that is comparable to the Sun. No nuclear fusion takes place i ...

s of low mass, according to the

of non- relativistic

degenerate matter Degenerate matter occurs when the Pauli exclusion principle significantly alters a state of matter at low temperature. The term is used in astrophysics to refer to dense stellar objects such as white dwarfs and neutron stars, where thermal press ...

.Sagert, I., Hempel, M., Greiner, C., Schaffner-Bielich, J. (2006). Compact stars for undergraduates. European journal of physics, 27(3), 577.
/ref> *A polytrope with index is a good model for the cores of white dwarfs of higher masses, according to the equation of state of relativistic

. *A polytrope with index is usually also used to model

main-sequence In astronomy, the main sequence is a classification of stars which appear on plots of stellar color versus brightness as a continuous and distinctive band. Stars on this band are known as main-sequence stars or dwarf stars, and positions of star ...

star A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sk ...

s like the

Sun The Sun is the star at the centre of the Solar System. It is a massive, nearly perfect sphere of hot plasma, heated to incandescence by nuclear fusion reactions in its core, radiating the energy from its surface mainly as visible light a ...

, at least in the

radiation zone A radiative zone is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiative zone in the form of ...

, corresponding to the Eddington standard model of

stellar structure Stellar structure models describe the internal structure of a star in detail and make predictions about the luminosity, the color and the future evolution of the star. Different classes and ages of stars have different internal structures, refle ...

.O. R. Pols (2011), Stellar Structure and Evolution, Astronomical Institute Utrecht, September 2011, pp. 64-68 *A polytrope with index has an infinite radius. It corresponds to the simplest plausible model of a self-consistent stellar system, first studied by

Arthur Schuster Sir Franz Arthur Friedrich Schuster (12 September 1851 – 14 October 1934) was a German-born British physicist known for his work in spectroscopy, electrochemistry, optics, X-radiography and the application of harmonic analysis to physics. S ...

in 1883, and it has an exact solution. *A polytrope with index corresponds to what is called an ''isothermal sphere'', that is an

isothermal An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the sys ...

self-gravitating sphere of gas, whose structure is identical to the structure of a collisionless system of stars like a

globular cluster A globular cluster is a spheroidal conglomeration of stars that is bound together by gravity, with a higher concentration of stars towards its center. It can contain anywhere from tens of thousands to many millions of member stars, all orbiting ...

. This is because for an ideal gas, the temperature is proportional to ρ^1/n, so infinite ''n'' corresponds to a constant temperature. In general as the polytropic index increases, the density distribution is more heavily weighted toward the center () of the body.

References

{{reflist, colwidth=35em Astrophysics de:Polytrop

Example models by polytropic index

See also

References