electron tunneling on:
[Wikipedia]
[Google]
[Amazon]
In physics, quantum tunnelling, barrier penetration, or simply tunnelling is a quantum mechanical phenomenon in which an object such as an electron or atom passes through a potential energy barrier that, according to
 The
The


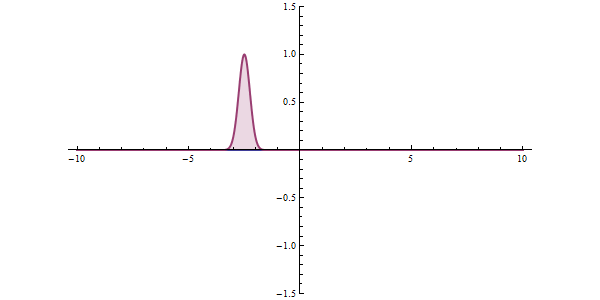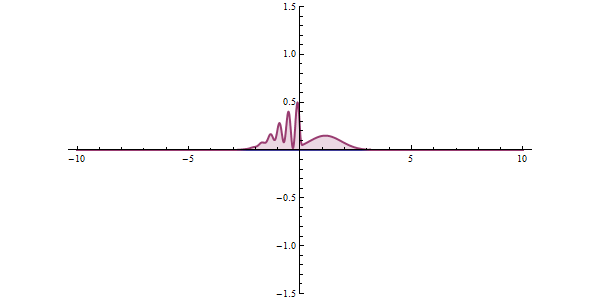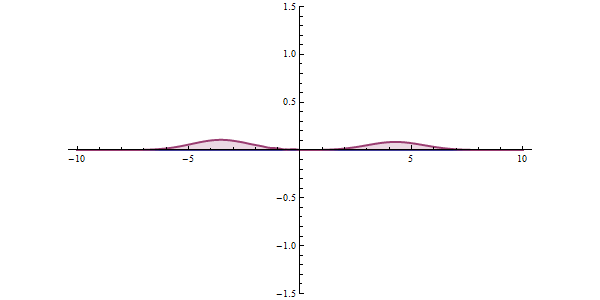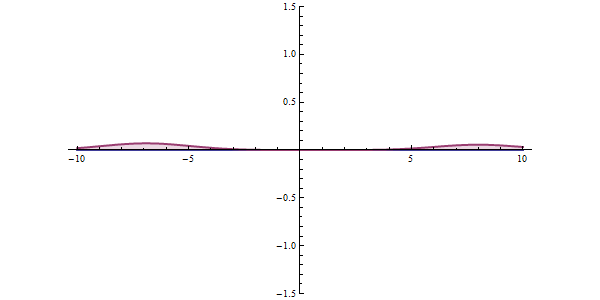 With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
 The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunnelling.
The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunnelling.
 In real life, most systems are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunnelling between them. This phenomenon is referred as chaos-assisted tunnelling. and is characterized by sharp resonances of the tunnelling rate when varying any system parameter.
In real life, most systems are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunnelling between them. This phenomenon is referred as chaos-assisted tunnelling. and is characterized by sharp resonances of the tunnelling rate when varying any system parameter.
Animation, applications and research linked to tunnel effect and other quantum phenomena
(Université Paris Sud)
Animated illustration of quantum tunneling in a RTD device
Interactive Solution of Schrodinger Tunnel Equation
{{Authority control Articles containing video clips Particle physics Quantum mechanics Solid state engineering
classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
, should not be passable due to the object not having sufficient energy to pass or surmount the barrier.
Tunneling is a consequence of the wave nature of matter, where the quantum wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
describes the state of a particle or other physical system
A physical system is a collection of physical objects under study. The collection differs from a set: all the objects must coexist and have some physical relationship.
In other words, it is a portion of the physical universe chosen for analys ...
, and wave equations such as the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
describe their behavior. The probability of transmission of a wave packet
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an Envelope (waves), envelope. A wave packet can be analyzed into, or can be synthesized from, a ...
through a barrier decreases exponentially with the barrier height, the barrier width, and the tunneling particle's mass, so tunneling is seen most prominently in low-mass particles such as electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s or proton
A proton is a stable subatomic particle, symbol , Hydron (chemistry), H+, or 1H+ with a positive electric charge of +1 ''e'' (elementary charge). Its mass is slightly less than the mass of a neutron and approximately times the mass of an e ...
s tunneling through microscopically narrow barriers. Tunneling is readily detectable with barriers of thickness about 1–3 nm or smaller for electrons, and about 0.1 nm or smaller for heavier particles such as protons or hydrogen atoms. Some sources describe the mere penetration of a wave function into the barrier, without transmission on the other side, as a tunneling effect, such as in tunneling into the walls of a finite potential well.
Tunneling plays an essential role in physical phenomena such as nuclear fusion
Nuclear fusion is a nuclear reaction, reaction in which two or more atomic nuclei combine to form a larger nuclei, nuclei/neutrons, neutron by-products. The difference in mass between the reactants and products is manifested as either the rele ...
and alpha radioactive decay of atomic nuclei. Tunneling applications include the tunnel diode, quantum computing
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of wave-particle duality, both particles and waves, and quantum computing takes advantage of this behavior using s ...
, flash memory
Flash memory is an Integrated circuit, electronic Non-volatile memory, non-volatile computer memory storage medium that can be electrically erased and reprogrammed. The two main types of flash memory, NOR flash and NAND flash, are named for t ...
, and the scanning tunneling microscope. Tunneling limits the minimum size of devices used in microelectronics
Microelectronics is a subfield of electronics. As the name suggests, microelectronics relates to the study and manufacture (or microfabrication) of very small electronic designs and components. Usually, but not always, this means micrometre ...
because electrons tunnel readily through insulating layers and transistor
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch electrical signals and electric power, power. It is one of the basic building blocks of modern electronics. It is composed of semicondu ...
s that are thinner than about 1 nm.
The effect was predicted in the early 20th century. Its acceptance as a general physical phenomenon came mid-century.
Introduction to the concept
Quantum tunnelling falls under the domain ofquantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. To understand the phenomenon
A phenomenon ( phenomena), sometimes spelled phaenomenon, is an observable Event (philosophy), event. The term came into its modern Philosophy, philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which ''cannot'' be ...
, particles attempting to travel across a potential barrier can be compared to a ball trying to roll over a hill. Quantum mechanics and classical mechanics differ in their treatment of this scenario.
Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier cannot reach the other side. Thus, a ball without sufficient energy to surmount the hill would roll back down. In quantum mechanics, a particle can, with a small probability, ''tunnel'' to the other side, thus crossing the barrier. The reason for this difference comes from treating matter as having properties of waves and particles.
Tunnelling problem
 The
The wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
of a physical system
A physical system is a collection of physical objects under study. The collection differs from a set: all the objects must coexist and have some physical relationship.
In other words, it is a portion of the physical universe chosen for analys ...
of particles specifies everything that can be known about the system. Therefore, problems in quantum mechanics analyze the system's wave function. Using mathematical formulations, such as the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
, the time evolution of a known wave function can be deduced. The square of the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of this wave function is directly related to the probability distribution of the particle positions, which describes the probability that the particles would be measured at those positions.
As shown in the animation, when a wave packet impinges on the barrier, most of it is reflected and some is transmitted through the barrier. The wave packet becomes more de-localized: it is now on both sides of the barrier and lower in maximum amplitude, but equal in integrated square-magnitude, meaning that the probability the particle is ''somewhere'' remains unity. The wider the barrier and the higher the barrier energy, the lower the probability of tunneling.
Some models of a tunneling barrier, such as the rectangular barriers shown, can be analysed and solved algebraically. Most problems do not have an algebraic solution, so numerical solutions are used. " Semiclassical methods" offer approximate solutions that are easier to compute, such as the WKB approximation.
History
The Schrödinger equation was published in 1926. The first person to apply the Schrödinger equation to a problem that involved tunneling between two classically allowed regions through a potential barrier was Friedrich Hund in a series of articles published in 1927. He studied the solutions of a double-well potential and discussedmolecular spectra
The emission spectrum of a chemical element or chemical compound is the Spectrum (physical sciences), spectrum of frequencies of electromagnetic radiation emitted due to electrons making a atomic electron transition, transition from a high energ ...
. Leonid Mandelstam and Mikhail Leontovich discovered tunneling independently and published their results in 1928.
In 1927, Lothar Nordheim, assisted by Ralph Fowler, published a paper that discussed thermionic emission
Thermionic emission is the liberation of charged particles from a hot electrode whose thermal energy gives some particles enough kinetic energy to escape the material's surface. The particles, sometimes called ''thermions'' in early literature, a ...
and reflection of electrons from metals. He assumed a surface potential barrier that confines the electrons within the metal and showed that the electrons have a finite probability of tunneling through or reflecting from the surface barrier when their energies are close to the barrier energy. Classically, the electron would either transmit or reflect with 100% certainty, depending on its energy. In 1928 J. Robert Oppenheimer
J. Robert Oppenheimer (born Julius Robert Oppenheimer ; April 22, 1904 – February 18, 1967) was an American theoretical physics, theoretical physicist who served as the director of the Manhattan Project's Los Alamos Laboratory during World ...
published two papers on field emission, ''i.e.'' the emission of electrons induced by strong electric fields. Nordheim and Fowler simplified Oppenheimer's derivation and found values for the emitted currents and work function
In solid-state physics, the work function (sometimes spelled workfunction) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here "immediately" ...
s that agreed with experiments.
A great success of the tunnelling theory was the mathematical explanation for alpha decay
Alpha decay or α-decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle (helium nucleus). The parent nucleus transforms or "decays" into a daughter product, with a mass number that is reduced by four and an a ...
, which was developed in 1928 by George Gamow and independently by Ronald Gurney and Edward Condon. The latter researchers simultaneously solved the Schrödinger equation for a model nuclear potential and derived a relationship between the half-life Half-life is a mathematical and scientific description of exponential or gradual decay.
Half-life, half life or halflife may also refer to:
Film
* Half-Life (film), ''Half-Life'' (film), a 2008 independent film by Jennifer Phang
* ''Half Life: ...
of the particle and the energy of emission that depended directly on the mathematical probability of tunneling. All three researchers were familiar with the works on field emission, and Gamow was aware of Mandelstam and Leontovich's findings.
In the early days of quantum theory, the term ''tunnel effect'' was not used, and the effect was instead referred to as penetration of, or leaking through, a barrier. The German term ''wellenmechanische Tunneleffekt'' was used in 1931 by Walter Schottky. The English term ''tunnel effect'' entered the language in 1932 when it was used by Yakov Frenkel in his textbook.
In 1957 Leo Esaki demonstrated tunneling of electrons over a few nanometer wide barrier in a semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level ...
structure and developed a diode
A diode is a two-Terminal (electronics), terminal electronic component that conducts electric current primarily in One-way traffic, one direction (asymmetric electrical conductance, conductance). It has low (ideally zero) Electrical resistance ...
based on tunnel effect. In 1960, following Esaki's work, Ivar Giaever showed experimentally that tunnelling also took place in superconductors
Superconductivity is a set of physical properties observed in superconductors: materials where electrical resistance vanishes and magnetic fields are expelled from the material. Unlike an ordinary metallic conductor, whose resistance decreases ...
. The tunnelling spectrum gave direct evidence of the superconducting energy gap. In 1962, Brian Josephson predicted the tunneling of superconducting Cooper pair
In condensed matter physics, a Cooper pair or BCS pair (Bardeen–Cooper–Schrieffer pair) is a pair of electrons (or other fermions) bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper. ...
s. Esaki, Giaever and Josephson shared the 1973 Nobel Prize in Physics
The Nobel Prize in Physics () is an annual award given by the Royal Swedish Academy of Sciences for those who have made the most outstanding contributions to mankind in the field of physics. It is one of the five Nobel Prizes established by the ...
for their works on quantum tunneling in solids.
In 1981, Gerd Binnig and Heinrich Rohrer
Heinrich Rohrer (6 June 1933 – 16 May 2013) was a Swiss physicist who shared half of the 1986 Nobel Prize in Physics with Gerd Binnig for the design of the scanning tunneling microscope (STM). The other half of the Prize was awarded to Ernst R ...
developed a new type of microscope, called scanning tunneling microscope, which is based on tunnelling and is used for imaging surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
s at the atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
ic level. Binnig and Rohrer were awarded the Nobel Prize in Physics in 1986 for their discovery.
Applications
Tunnelling is the cause of some important macroscopic physical phenomena.Solid-state physics
Electronics
Tunnelling is a source of current leakage in very-large-scale integration (VLSI) electronics and results in a substantial power drain and heating effects that plague such devices. It is considered the lower limit on how microelectronic device elements can be made. Tunnelling is a fundamental technique used to program the floating gates offlash memory
Flash memory is an Integrated circuit, electronic Non-volatile memory, non-volatile computer memory storage medium that can be electrically erased and reprogrammed. The two main types of flash memory, NOR flash and NAND flash, are named for t ...
.
Cold emission
Cold emission ofelectrons
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
is relevant to semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level ...
s and superconductor physics. It is similar to thermionic emission
Thermionic emission is the liberation of charged particles from a hot electrode whose thermal energy gives some particles enough kinetic energy to escape the material's surface. The particles, sometimes called ''thermions'' in early literature, a ...
, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field. These materials are important for flash memory, vacuum tubes, and some electron microscopes.
Tunnel junction
A simple barrier can be created by separating two conductors with a very thin insulator. These are tunnel junctions, the study of which requires understanding quantum tunnelling. Josephson junctions take advantage of quantum tunnelling and superconductivity to create theJosephson effect
In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. The effect is named after the British physicist Brian Josephson, who predicted in 1962 ...
. This has applications in precision measurements of voltages and magnetic fields
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
, as well as the multijunction solar cell.
Tunnel diode

Diode
A diode is a two-Terminal (electronics), terminal electronic component that conducts electric current primarily in One-way traffic, one direction (asymmetric electrical conductance, conductance). It has low (ideally zero) Electrical resistance ...
s are electrical semiconductor device
A semiconductor device is an electronic component that relies on the electronic properties of a semiconductor material (primarily silicon, germanium, and gallium arsenide, as well as organic semiconductors) for its function. Its conductivit ...
s that allow electric current
An electric current is a flow of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is defined as the net rate of flow of electric charge through a surface. The moving particles are called charge c ...
flow in one direction more than the other. The device depends on a depletion layer between N-type and P-type semiconductors to serve its purpose. When these are heavily doped the depletion layer can be thin enough for tunnelling. When a small forward bias is applied, the current due to tunnelling is significant. This has a maximum at the point where the voltage bias is such that the energy level of the p and n conduction bands are the same. As the voltage bias is increased, the two conduction bands no longer line up and the diode acts typically.
Because the tunnelling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage increases. This peculiar property is used in some applications, such as high speed devices where the characteristic tunnelling probability changes as rapidly as the bias voltage.
The resonant tunnelling diode makes use of quantum tunnelling in a very different manner to achieve a similar result. This diode has a resonant voltage for which a current favors a particular voltage, achieved by placing two thin layers with a high energy conductance band near each other. This creates a quantum potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy ( kinetic energy in the case of a gravitational potential well) because it is cap ...
that has a discrete lowest energy level
A quantum mechanics, quantum mechanical system or particle that is bound state, bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical mechanics, classical pa ...
. When this energy level is higher than that of the electrons, no tunnelling occurs and the diode is in reverse bias. Once the two voltage energies align, the electrons flow like an open wire. As the voltage further increases, tunnelling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.
Tunnel field-effect transistors
A European research project demonstrated field effect transistors in which the gate (channel) is controlled via quantum tunnelling rather than by thermal injection, reducing gate voltage from ≈1 volt to 0.2 volts and reducing power consumption by up to 100×. If these transistors can be scaled up into VLSI chips, they would improve the performance per power ofintegrated circuit
An integrated circuit (IC), also known as a microchip or simply chip, is a set of electronic circuits, consisting of various electronic components (such as transistors, resistors, and capacitors) and their interconnections. These components a ...
s.
Conductivity of crystalline solids
While the Drude-Lorentz model ofelectrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunnelling to explain the nature of the electron's collisions. When a free electron wave packet encounters a long array of uniformly spaced barriers, the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that 100% transmission becomes possible. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to extremely high conductance, and that impurities in the metal will disrupt it.
Scanning tunneling microscope
The scanning tunnelling microscope (STM), invented by Gerd Binnig andHeinrich Rohrer
Heinrich Rohrer (6 June 1933 – 16 May 2013) was a Swiss physicist who shared half of the 1986 Nobel Prize in Physics with Gerd Binnig for the design of the scanning tunneling microscope (STM). The other half of the Prize was awarded to Ernst R ...
, may allow imaging of individual atoms on the surface of a material. It operates by taking advantage of the relationship between quantum tunnelling with distance. When the tip of the STM's needle is brought close to a conduction surface that has a voltage bias, measuring the current of electrons that are tunnelling between the needle and the surface reveals the distance between the needle and the surface. By using piezoelectric rods that change in size when voltage is applied, the height of the tip can be adjusted to keep the tunnelling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor. STMs are accurate to 0.001 nm, or about 1% of atomic diameter.
Nuclear physics
Nuclear fusion
Quantum tunnelling is an essential phenomenon for nuclear fusion. The temperature in stellar cores is generally insufficient to allow atomic nuclei to overcome the Coulomb barrier and achievethermonuclear fusion
Nuclear fusion is a reaction in which two or more atomic nuclei combine to form a larger nuclei, nuclei/neutron by-products. The difference in mass between the reactants and products is manifested as either the release or absorption of ener ...
. Quantum tunnelling increases the probability of penetrating this barrier. Though this probability is still low, the extremely large number of nuclei in the core of a star is sufficient to sustain a steady fusion reaction.
Radioactive decay
Radioactive decay is the process of emission of particles and energy from the unstable nucleus of an atom to form a stable product. This is done via the tunnelling of a particle out of the nucleus (an electron tunneling into the nucleus iselectron capture
Electron capture (K-electron capture, also K-capture, or L-electron capture, L-capture) is a process in which the proton-rich nucleus of an electrically neutral atom absorbs an inner atomic electron, usually from the K or L electron shells. Th ...
). This was the first application of quantum tunnelling. Radioactive decay is a relevant issue for astrobiology
Astrobiology (also xenology or exobiology) is a scientific field within the List of life sciences, life and environmental sciences that studies the abiogenesis, origins, Protocell, early evolution, distribution, and future of life in the univ ...
as this consequence of quantum tunnelling creates a constant energy source over a large time interval for environments outside the circumstellar habitable zone where insolation would not be possible ( subsurface oceans) or effective.
Quantum tunnelling may be one of the mechanisms of hypothetical proton decay.ucl-th/9809006Time-dependent properties of proton decay from crossing single-particle metastable states in deformed nuclei">
Chemistry
Energetically forbidden reactions
Chemical reactions in theinterstellar medium
The interstellar medium (ISM) is the matter and radiation that exists in the outer space, space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, as well as cosmic dust, dust and cosmic rays. It f ...
occur at extremely low energies. Probably the most fundamental ion-molecule reaction involves hydrogen ions with hydrogen molecules.
The quantum mechanical tunnelling rate for the same reaction using the hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
isotope deuterium
Deuterium (hydrogen-2, symbol H or D, also known as heavy hydrogen) is one of two stable isotopes of hydrogen; the other is protium, or hydrogen-1, H. The deuterium nucleus (deuteron) contains one proton and one neutron, whereas the far more c ...
, D− + H2 → H− + HD, has been measured experimentally in an ion trap.
The deuterium was placed in an ion trap
An ion trap is a combination of electric field, electric and/or magnetic fields used to capture charged particles — known as ions — often in a system isolated from an external environment. Atomic and molecular ion traps have a number of a ...
and cooled. The trap was then filled with hydrogen. At the temperatures used in the experiment, the energy barrier for reaction would not allow the reaction to succeed with classical dynamics alone. Quantum tunneling allowed reactions to happen in rare collisions. It was calculated from the experimental data that collisions happened one in every hundred billion.
Kinetic isotope effect
Inchemical kinetics
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is different from chemical thermodynamics, which deals with the direction in which a ...
, the substitution of a light isotope
Isotopes are distinct nuclear species (or ''nuclides'') of the same chemical element. They have the same atomic number (number of protons in their Atomic nucleus, nuclei) and position in the periodic table (and hence belong to the same chemica ...
of an element with a heavier one typically results in a slower reaction rate. This is generally attributed to differences in the zero-point vibrational energies for chemical bonds containing the lighter and heavier isotopes and is generally modeled using transition state theory. However, in certain cases, large isotopic effects are observed that cannot be accounted for by a semi-classical treatment, and quantum tunnelling is required. R. P. Bell developed a modified treatment of Arrhenius kinetics that is commonly used to model this phenomenon.
Astrochemistry in interstellar clouds
By including quantum tunnelling, the astrochemical syntheses of various molecules in interstellar clouds can be explained, such as the synthesis ofmolecular hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
, water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
(ice
Ice is water that is frozen into a solid state, typically forming at or below temperatures of 0 ° C, 32 ° F, or 273.15 K. It occurs naturally on Earth, on other planets, in Oort cloud objects, and as interstellar ice. As a naturally oc ...
) and the prebiotic important formaldehyde
Formaldehyde ( , ) (systematic name methanal) is an organic compound with the chemical formula and structure , more precisely . The compound is a pungent, colourless gas that polymerises spontaneously into paraformaldehyde. It is stored as ...
. Tunnelling of molecular hydrogen has been observed in the lab.
Quantum biology
Quantum tunnelling is among the central non-trivial quantum effects inquantum biology
Quantum biology is the study of applications of quantum mechanics and theoretical chemistry to aspects of biology that cannot be accurately described by the classical laws of physics. An understanding of fundamental quantum interactions is importan ...
. Here it is important both as electron tunnelling and proton tunnelling. Electron tunnelling is a key factor in many biochemical redox reactions
Redox ( , , reduction–oxidation or oxidation–reduction) is a type of chemical reaction in which the oxidation states of the reactants change. Oxidation is the loss of electrons or an increase in the oxidation state, while reduction is ...
(photosynthesis
Photosynthesis ( ) is a system of biological processes by which photosynthetic organisms, such as most plants, algae, and cyanobacteria, convert light energy, typically from sunlight, into the chemical energy necessary to fuel their metabo ...
, cellular respiration
Cellular respiration is the process of oxidizing biological fuels using an inorganic electron acceptor, such as oxygen, to drive production of adenosine triphosphate (ATP), which stores chemical energy in a biologically accessible form. Cell ...
) as well as enzymatic catalysis. Proton tunnelling is a key factor in spontaneous DNA
Deoxyribonucleic acid (; DNA) is a polymer composed of two polynucleotide chains that coil around each other to form a double helix. The polymer carries genetic instructions for the development, functioning, growth and reproduction of al ...
mutation.
Spontaneous mutation occurs when normal DNA replication takes place after a particularly significant proton has tunnelled. A hydrogen bond joins DNA base pairs. A double well potential along a hydrogen bond separates a potential energy barrier. It is believed that the double well potential is asymmetric, with one well deeper than the other such that the proton normally rests in the deeper well. For a mutation to occur, the proton must have tunnelled into the shallower well. The proton's movement from its regular position is called a tautomeric transition. If DNA replication takes place in this state, the base pairing rule for DNA may be jeopardised, causing a mutation. Per-Olov Lowdin was the first to develop this theory of spontaneous mutation within the double helix
In molecular biology, the term double helix refers to the structure formed by base pair, double-stranded molecules of nucleic acids such as DNA. The double Helix, helical structure of a nucleic acid complex arises as a consequence of its Nuclei ...
. Other instances of quantum tunnelling-induced mutations in biology are believed to be a cause of ageing and cancer.
Mathematical discussion
Schrödinger equation
The time-independent Schrödinger equation for one particle in onedimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
can be written as
or
where
* is the reduced Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
,
* ''m'' is the particle mass,
* ''x'' represents distance measured in the direction of motion of the particle,
* Ψ is the Schrödinger wave function,
* ''V'' is the potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
of the particle (measured relative to any convenient reference level),
* ''E'' is the energy of the particle that is associated with motion in the ''x''-axis (measured relative to ''V''),
* ''M''(''x'') is a quantity defined by ''V''(''x'') − ''E'', which has no accepted name in physics.
The solutions of the Schrödinger equation take different forms for different values of ''x'', depending on whether ''M''(''x'') is positive or negative. When ''M''(''x'') is constant and negative, then the Schrödinger equation can be written in the form
The solutions of this equation represent travelling waves, with phase-constant +''k'' or −''k''. Alternatively, if ''M''(''x'') is constant and positive, then the Schrödinger equation can be written in the form
The solutions of this equation are rising and falling exponentials in the form of evanescent waves. When ''M''(''x'') varies with position, the same difference in behaviour occurs, depending on whether M(x) is negative or positive. It follows that the sign of ''M''(''x'') determines the nature of the medium, with negative ''M''(''x'') corresponding to medium A and positive ''M''(''x'') corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive ''M''(''x'') is sandwiched between two regions of negative ''M''(''x''), hence creating a potential barrier.
The mathematics of dealing with the situation where ''M''(''x'') varies with ''x'' is difficult, except in special cases that usually do not correspond to physical reality. A full mathematical treatment appears in the 1965 monograph by Fröman and Fröman. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.
WKB approximation
The wave function is expressed as the exponential of a function: where is then separated into real and imaginary parts: where ''A''(''x'') and ''B''(''x'') are real-valued functions. Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in: To solve this equation using the semiclassical approximation, each function must be expanded as apower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
in . From the equations, the power series must start with at least an order of to satisfy the real part of the equation; for a good classical limit starting with the highest power of the Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
possible is preferable, which leads to
and
with the following constraints on the lowest order terms,
and
At this point two extreme cases can be considered.
Case 1
If the amplitude varies slowly as compared to the phase and
which corresponds to classical motion. Resolving the next order of expansion yields
Case 2
If the phase varies slowly as compared to the amplitude, and
which corresponds to tunneling. Resolving the next order of the expansion yields
In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points . Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.
To start, a classical turning point, is chosen and is expanded in a power series about :
Keeping only the first order term ensures linearity:
Using this approximation, the equation near becomes a differential equation:
This can be solved using Airy function
In the physical sciences, the Airy function (or Airy function of the first kind) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(''x'') and the related function Bi(''x''), are Linear in ...
s as solutions.
Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the two coefficients on one side of a classical turning point, the two coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.
Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between and are
and
: 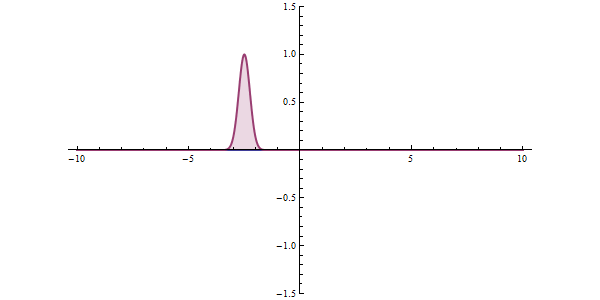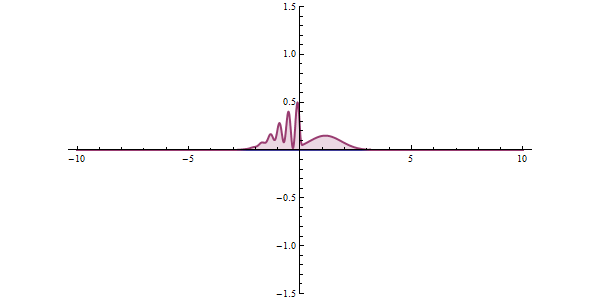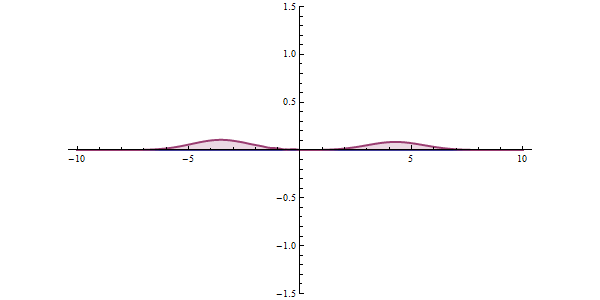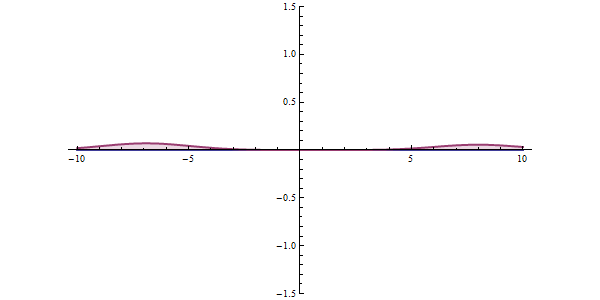 With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
Faster than light
Some physicists have claimed that it is possible for spin-zero particles to travel faster than thespeed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
when tunnelling. This appears to violate the principle of causality, since a frame of reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin (mathematics), origin, orientation (geometry), orientation, and scale (geometry), scale have been specified in physical space. It ...
then exists in which the particle arrives before it has left. In 1998, Francis E. Low reviewed briefly the phenomenon of zero-time tunnelling. More recently, experimental tunnelling time data of phonons
A phonon is a collective excitation in a periodic, Elasticity (physics), elastic arrangement of atoms or molecules in condensed matter physics, condensed matter, specifically in solids and some liquids. In the context of optically trapped objects ...
, photons
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that ...
, and electrons
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
was published by Günter Nimtz. Another experiment overseen by A. M. Steinberg, seems to indicate that particles could tunnel at apparent speeds faster than light.
Other physicists, such as Herbert Winful, disputed these claims. Winful argued that the wave packet of a tunnelling particle propagates locally, so a particle can't tunnel through the barrier non-locally. Winful also argued that the experiments that are purported to show non-local propagation have been misinterpreted. In particular, the group velocity of a wave packet does not measure its speed, but is related to the amount of time the wave packet is stored in the barrier. Moreover, if quantum tunneling is modeled with the relativistic Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac ...
, well established mathematical theorems imply that the process is completely subluminal.
Dynamical tunneling
 The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunnelling.
The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunnelling.
Tunnelling in phase space
The concept of dynamical tunnelling is particularly suited to address the problem of quantum tunnelling in high dimensions (d>1). In the case of an integrable system, where bounded classical trajectories are confined onto tori inphase space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the p ...
, tunnelling can be understood as the quantum transport between semi-classical states built on two distinct but symmetric tori.
Chaos-assisted tunnelling
 In real life, most systems are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunnelling between them. This phenomenon is referred as chaos-assisted tunnelling. and is characterized by sharp resonances of the tunnelling rate when varying any system parameter.
In real life, most systems are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunnelling between them. This phenomenon is referred as chaos-assisted tunnelling. and is characterized by sharp resonances of the tunnelling rate when varying any system parameter.
Resonance-assisted tunnelling
When is small in front of the size of the regular islands, the fine structure of the classical phase space plays a key role in tunnelling. In particular the two symmetric tori are coupled "via a succession of classically forbidden transitions across nonlinear resonances" surrounding the two islands.Related phenomena
Several phenomena have the same behavior as quantum tunnelling. Two examples are evanescent wave coupling (the application of Maxwell's wave-equation tolight
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
) and the application of the non-dispersive wave-equation from acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
applied to "waves on strings".
These effects are modeled similarly to the rectangular potential barrier. In these cases, one transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modula ...
through which the wave propagates that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential solutions in medium B.
In optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy is greater than its potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete. Approximations are useful in this case.
A classical wave-particle association was originally analyzed as analogous to quantum tunneling, but subsequent analysis found a fluid dynamics cause related to the vertical momentum imparted to particles near the barrier.
See also
* Dielectric barrier discharge *Field electron emission
Field electron emission, also known as field-induced electron emission, field emission (FE) and electron field emission, is the emission of electrons from a material placed in an electrostatic field. The most common context is field emission from ...
* Holstein–Herring method
* Proton tunneling
* Quantum cloning
* Superconducting tunnel junction
* Tunnel diode
* Tunnel junction
In electronics, a tunnel junction is a barrier, such as a thin insulating layer or electric potential, between two electrically conducting materials. Electrons (or quasiparticles) pass through the barrier by the process of quantum tunnelling. Clas ...
* White hole
In general relativity, a white hole is a hypothetical region of spacetime and Gravitational singularity, singularity that cannot be entered from the outside, although energy, matter, light and information can escape from it. In this sense, it is ...
References
Further reading
* * * * * * * *External links
Animation, applications and research linked to tunnel effect and other quantum phenomena
(Université Paris Sud)
Animated illustration of quantum tunneling in a RTD device
Interactive Solution of Schrodinger Tunnel Equation
{{Authority control Articles containing video clips Particle physics Quantum mechanics Solid state engineering