Conjectures on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, a conjecture is a conclusion or a
In mathematics, a conjecture is a conclusion or a
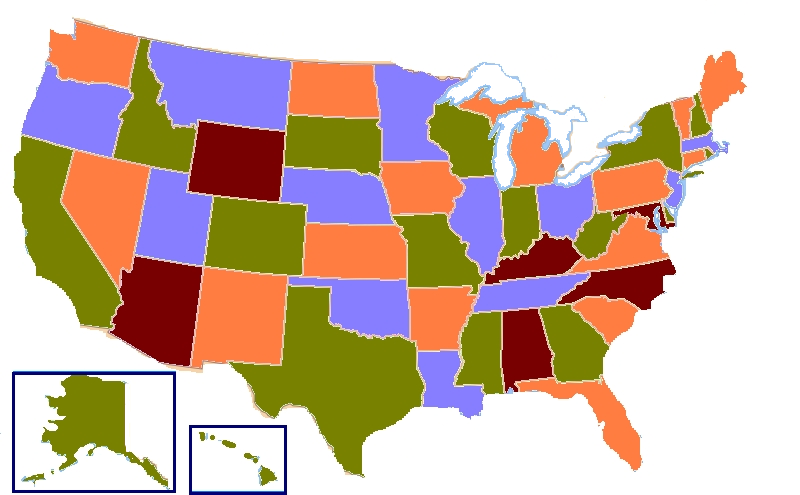 In mathematics, the
In mathematics, the
Open Problem GardenUnsolved Problems web site
{{Portal bar, Mathematics, Science Concepts in the philosophy of science Statements Mathematical terminology
proposition
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, "meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the no ...
that is proffered on a tentative basis without proof
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a con ...
. Some conjectures, such as the Riemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pu ...
(still a conjecture) or Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers , , and satisfy the equation for any integer value of greater than 2. The cases and have bee ...
(a conjecture until proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.
Important examples
Fermat's Last Theorem
Innumber theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Math ...
, Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers , , and satisfy the equation for any integer value of greater than 2. The cases and have bee ...
(sometimes called Fermat's conjecture, especially in older texts) states that no three positive integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s , '''', and '''' can satisfy the equation '''' for any integer value of '''' greater than two.
This theorem was first conjectured by Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
in 1637 in the margin of a copy of ''Arithmetica
''Arithmetica'' ( grc-gre, Ἀριθμητικά) is an Ancient Greek text on mathematics written by the mathematician Diophantus () in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate e ...
'', where he claimed that he had a proof that was too large to fit in the margin. The first successful proof was released in 1994 by Andrew Wiles, and formally published in 1995, after 358 years of effort by mathematicians. The unsolved problem stimulated the development of algebraic number theory in the 19th century, and the proof of the modularity theorem in the 20th century. It is among the most notable theorems in the history of mathematics, and prior to its proof it was in the ''Guinness Book of World Records
''Guinness World Records'', known from its inception in 1955 until 1999 as ''The Guinness Book of Records'' and in previous United States editions as ''The Guinness Book of World Records'', is a reference book published annually, listing world ...
'' for "most difficult mathematical problems".
Four color theorem
 In mathematics, the
In mathematics, the four color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions sh ...
, or the four color map theorem, states that given any separation of a plane into contiguous regions, producing a figure called a ''map'', no more than four colors are required to color the regions of the map—so that no two adjacent regions have the same color. Two regions are called ''adjacent'' if they share a common boundary that is not a corner, where corners are the points shared by three or more regions. For example, in the map of the United States of America, Utah and Arizona are adjacent, but Utah and New Mexico, which only share a point that also belongs to Arizona and Colorado, are not.
Möbius mentioned the problem in his lectures as early as 1840.W. W. Rouse Ball
Walter William Rouse Ball (14 August 1850 – 4 April 1925), known as W. W. Rouse Ball, was a British mathematician, lawyer, and fellow at Trinity College, Cambridge, from 1878 to 1905. He was also a keen amateur magician, and the founding ...
(1960) ''The Four Color Theorem'', in Mathematical Recreations and Essays, Macmillan, New York, pp 222-232. The conjecture was first proposed on October 23, 1852Donald MacKenzie, ''Mechanizing Proof: Computing, Risk, and Trust'' (MIT Press, 2004) p103 when Francis Guthrie
Francis Guthrie (born 22 January 1831 in London; d. 19 October 1899 in Claremont, Cape Town) was a South African mathematician and botanist who first posed the Four Colour Problem in 1852. He studied mathematics under Augustus De Morgan, and ...
, while trying to color the map of counties of England, noticed that only four different colors were needed. The five color theorem, which has a short elementary proof, states that five colors suffice to color a map and was proven in the late 19th century; however, proving that four colors suffice turned out to be significantly harder. A number of false proofs and false counterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "John Smith is not a lazy student" is ...
s have appeared since the first statement of the four color theorem in 1852.
The four color theorem was ultimately proven in 1976 by Kenneth Appel and Wolfgang Haken. It was the first major theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of ...
to be proved using a computer. Appel and Haken's approach started by showing that there is a particular set of 1,936 maps, each of which cannot be part of a smallest-sized counterexample to the four color theorem (i.e., if they did appear, one could make a smaller counter-example). Appel and Haken used a special-purpose computer program to confirm that each of these maps had this property. Additionally, any map that could potentially be a counterexample must have a portion that looks like one of these 1,936 maps. Showing this with hundreds of pages of hand analysis, Appel and Haken concluded that no smallest counterexample exists because any must contain, yet do not contain, one of these 1,936 maps. This contradiction means there are no counterexamples at all and that the theorem is therefore true. Initially, their proof was not accepted by mathematicians at all because the computer-assisted proof was infeasible for a human to check by hand. However, the proof has since then gained wider acceptance, although doubts still remain.
Hauptvermutung
The Hauptvermutung (German for main conjecture) ofgeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topology may be said to have originat ...
is the conjecture that any two triangulations of a triangulable space have a common refinement, a single triangulation that is a subdivision of both of them. It was originally formulated in 1908, by Steinitz and Tietze.
This conjecture is now known to be false. The non-manifold version was disproved by John Milnor in 1961 using Reidemeister torsion
In mathematics, Reidemeister torsion (or R-torsion, or Reidemeister–Franz torsion) is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by and .
Analytic torsion (or Ray– ...
.
The manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a ...
version is true in dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coor ...
s . The cases were proved by Tibor Radó
Tibor Radó (June 2, 1895 – December 29, 1965) was a Hungarian mathematician who moved to the United States after World War I.
Biography
Radó was born in Budapest and between 1913 and 1915 attended the Polytechnic Institute, studying ...
and Edwin E. Moise
Edwin Evariste Moise (; December 22, 1918 – December 18, 1998)
was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th-century English poetry and had severa ...
in the 1920s and 1950s, respectively.
Weil conjectures
In mathematics, theWeil conjectures
In mathematics, the Weil conjectures were highly influential proposals by . They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
...
were some highly influential proposals by on the generating function
In mathematics, a generating function is a way of encoding an infinite sequence of numbers () by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary ser ...
s (known as local zeta-functions) derived from counting the number of points on algebraic varieties
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex number
...
over finite field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subt ...
s.
A variety ''V'' over a finite field with ''q'' elements has a finite number of rational points, as well as points over every finite field with ''q''''k'' elements containing that field. The generating function has coefficients derived from the numbers ''N''''k'' of points over the (essentially unique) field with ''q''''k'' elements.
Weil conjectured that such ''zeta-functions'' should be rational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be ...
s, should satisfy a form of functional equation
In mathematics, a functional equation
is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted mea ...
, and should have their zeroes in restricted places. The last two parts were quite consciously modeled on the Riemann zeta function and Riemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pu ...
. The rationality was proved by , the functional equation by , and the analogue of the Riemann hypothesis was proved by
Poincaré conjecture
In mathematics, thePoincaré conjecture
In the mathematical field of geometric topology, the Poincaré conjecture (, , ) is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.
Originally conjectured b ...
is a theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of ...
about the characterization
Characterization or characterisation is the representation of persons (or other beings or creatures) in narrative and dramatic works. The term character development is sometimes used as a synonym. This representation may include direct methods ...
of the 3-sphere, which is the hypersphere that bounds the unit ball
Unit may refer to:
Arts and entertainment
* UNIT, a fictional military organization in the science fiction television series ''Doctor Who''
* Unit of action, a discrete piece of action (or beat) in a theatrical presentation
Music
* ''Unit'' (al ...
in four-dimensional space. The conjecture states that: An equivalent form of the conjecture involves a coarser form of equivalence than homeomorphism called homotopy equivalence
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a defo ...
: if a 3-manifold is ''homotopy equivalent'' to the 3-sphere, then it is necessarily ''homeomorphic'' to it.
Originally conjectured by Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The ...
in 1904, the theorem concerns a space that locally looks like ordinary three-dimensional space but is connected, finite in size, and lacks any boundary (a closed 3-manifold). The Poincaré conjecture claims that if such a space has the additional property that each loop
Loop or LOOP may refer to:
Brands and enterprises
* Loop (mobile), a Bulgarian virtual network operator and co-founder of Loop Live
* Loop, clothing, a company founded by Carlos Vasquez in the 1990s and worn by Digable Planets
* Loop Mobile, ...
in the space can be continuously tightened to a point, then it is necessarily a three-dimensional sphere. An analogous result has been known in higher dimensions for some time.
After nearly a century of effort by mathematicians, Grigori Perelman
Grigori Yakovlevich Perelman ( rus, links=no, Григорий Яковлевич Перельман, p=ɡrʲɪˈɡorʲɪj ˈjakəvlʲɪvʲɪtɕ pʲɪrʲɪlʲˈman, a=Ru-Grigori Yakovlevich Perelman.oga; born 13 June 1966) is a Russian mathemati ...
presented a proof of the conjecture in three papers made available in 2002 and 2003 on arXiv
arXiv (pronounced " archive"—the X represents the Greek letter chi ⟨χ⟩) is an open-access repository of electronic preprints and postprints (known as e-prints) approved for posting after moderation, but not peer review. It consists o ...
. The proof followed on from the program of Richard S. Hamilton
Richard Streit Hamilton (born 10 January 1943) is an American mathematician who serves as the Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. Hamilton ...
to use the Ricci flow to attempt to solve the problem. Hamilton later introduced a modification of the standard Ricci flow, called ''Ricci flow with surgery'' to systematically excise singular regions as they develop, in a controlled way, but was unable to prove this method "converged" in three dimensions. Perelman completed this portion of the proof. Several teams of mathematicians have verified that Perelman's proof is correct.
The Poincaré conjecture, before being proven, was one of the most important open questions in topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ho ...
.
Riemann hypothesis
In mathematics, theRiemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pu ...
, proposed by , is a conjecture that the non-trivial zeros of the Riemann zeta function all have real part 1/2. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields.
The Riemann hypothesis implies results about the distribution of prime numbers. Along with suitable generalizations, some mathematicians consider it the most important unresolved problem in pure mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications ...
. The Riemann hypothesis, along with the Goldbach conjecture
Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.
The conjecture has been shown to hold ...
, is part of Hilbert's eighth problem
Hilbert's eighth problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns number theory, and in particular the Riemann hypothesis, although it is also concerned with the Goldbach Conjecture. The problem as st ...
in David Hilbert's list of 23 unsolved problems; it is also one of the Clay Mathematics Institute Millennium Prize Problems.
P versus NP problem
The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer; it is widely conjectured that the answer is no. It was essentially first mentioned in a 1956 letter written byKurt Gödel
Kurt Friedrich Gödel ( , ; April 28, 1906 – January 14, 1978) was a logician, mathematician, and philosopher. Considered along with Aristotle and Gottlob Frege to be one of the most significant logicians in history, Gödel had an imm ...
to John von Neumann
John von Neumann (; hu, Neumann János Lajos, ; December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. He was regarded as having perhaps the widest cove ...
. Gödel asked whether a certain NP-complete problem could be solved in quadratic or linear time. The precise statement of the P=NP problem was introduced in 1971 by Stephen Cook in his seminal paper "The complexity of theorem proving procedures" and is considered by many to be the most important open problem in the field. It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution.
Other conjectures
* Goldbach's conjecture * The twin prime conjecture * TheCollatz conjecture
The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of intege ...
* The Manin conjecture
* The Maldacena conjecture
Juan Martín Maldacena (born September 10, 1968) is an Argentine theoretical physicist and the Carl P. Feinberg Professor in the School of Natural Sciences at the Institute for Advanced Study, Princeton. He has made significant contributions to ...
* The Euler conjecture, proposed by Euler in the 18th century but for which counterexamples for a number of exponents (starting with n=4) were found beginning in the mid 20th century
* The Hardy-Littlewood conjectures are a pair of conjectures concerning the distribution of prime numbers, the first of which expands upon the aforementioned twin prime conjecture. Neither one has either been proven or disproven, but it ''has'' been proven that both cannot simultaneously be true (i.e., at least one must be false). It has not been proven which one is false, but it is widely believed that the first conjecture is true and the second one is false.
* The Langlands program is a far-reaching web of these ideas of ' unifying conjectures' that link different subfields of mathematics (e.g. between number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Math ...
and representation theory of Lie groups). Some of these conjectures have since been proved.
Resolution of conjectures
Proof
Formal mathematics is based on ''provable'' truth. In mathematics, any number of cases supporting a universally quantified conjecture, no matter how large, is insufficient for establishing the conjecture's veracity, since a singlecounterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "John Smith is not a lazy student" is ...
could immediately bring down the conjecture. Mathematical journals sometimes publish the minor results of research teams having extended the search for a counterexample farther than previously done. For instance, the Collatz conjecture
The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of intege ...
, which concerns whether or not certain sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called ...
s of integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s terminate, has been tested for all integers up to 1.2 × 1012 (over a trillion). However, the failure to find a counterexample after extensive search does not constitute a proof that the conjecture is true—because the conjecture might be false but with a very large minimal counterexample.
Nevertheless, mathematicians often regard a conjecture as strongly supported by evidence even though not yet proved. That evidence may be of various kinds, such as verification of consequences of it or strong interconnections with known results.
A conjecture is considered proven only when it has been shown that it is logically impossible for it to be false. There are various methods of doing so; see methods of mathematical proof for more details.
One method of proof, applicable when there are only a finite number of cases that could lead to counterexamples, is known as "brute force
Brute Force or brute force may refer to:
Techniques
* Brute force method or proof by exhaustion, a method of mathematical proof
* Brute-force attack, a cryptanalytic attack
* Brute-force search, a computer problem-solving technique
People
* Brut ...
": in this approach, all possible cases are considered and shown not to give counterexamples. In some occasions, the number of cases is quite large, in which case a brute-force proof may require as a practical matter the use of a computer algorithm to check all the cases. For example, the validity of the 1976 and 1997 brute-force proofs of the four color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions sh ...
by computer was initially doubted, but was eventually confirmed in 2005 by theorem-proving software.
When a conjecture has been proven
Proven is a rural village in the Belgian province of West Flanders, and a "deelgemeente" of the municipality Poperinge. The village has about 1400 inhabitants.
The church and parish of Proven are named after Saint Victor. The Saint Victor ...
, it is no longer a conjecture but a theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of ...
. Many important theorems were once conjectures, such as the Geometrization theorem (which resolved the Poincaré conjecture
In the mathematical field of geometric topology, the Poincaré conjecture (, , ) is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.
Originally conjectured b ...
), Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers , , and satisfy the equation for any integer value of greater than 2. The cases and have bee ...
, and others.
Disproof
Conjectures disproven through counterexample are sometimes referred to as ''false conjectures'' (cf. the Pólya conjecture andEuler's sum of powers conjecture
Euler's conjecture is a disproved conjecture in mathematics related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers and greater than 1, if the sum of many th powers of positive integers is ...
). In the case of the latter, the first counterexample found for the n=4 case involved numbers in the millions, although it has been subsequently found that the minimal counterexample is actually smaller.
Independent conjectures
Not every conjecture ends up being proven true or false. Thecontinuum hypothesis
In mathematics, the continuum hypothesis (abbreviated CH) is a hypothesis about the possible sizes of infinite sets. It states that
or equivalently, that
In Zermelo–Fraenkel set theory with the axiom of choice (ZFC), this is equivalent ...
, which tries to ascertain the relative cardinality
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set A = \ contains 3 elements, and therefore A has a cardinality of 3. Beginning in the late 19th century, this concept was generalized ...
of certain infinite set
In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable.
Properties
The set of natural numbers (whose existence is postulated by the axiom of infinity) is infinite. It is the only ...
s, was eventually shown to be independent
Independent or Independents may refer to:
Arts, entertainment, and media Artist groups
* Independents (artist group), a group of modernist painters based in the New Hope, Pennsylvania, area of the United States during the early 1930s
* Independe ...
from the generally accepted set of Zermelo–Fraenkel axioms of set theory. It is therefore possible to adopt this statement, or its negation, as a new axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy o ...
in a consistent manner (much as Euclid
Euclid (; grc-gre, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Elements'' treatise, which established the foundations of ...
's parallel postulate can be taken either as true or false in an axiomatic system for geometry).
In this case, if a proof uses this statement, researchers will often look for a new proof that ''doesn't'' require the hypothesis (in the same way that it is desirable that statements in Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
be proved using only the axioms of neutral geometry, i.e. without the parallel postulate). The one major exception to this in practice is the axiom of choice
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that ''a Cartesian product of a collection of non-empty sets is non-empty''. Informally put, the axiom of choice says that given any collection ...
, as the majority of researchers usually do not worry whether a result requires it—unless they are studying this axiom in particular.
Conditional proofs
Sometimes, a conjecture is called a ''hypothesis'' when it is used frequently and repeatedly as an assumption in proofs of other results. For example, theRiemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pu ...
is a conjecture from number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Math ...
that — amongst other things — makes predictions about the distribution of prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only way ...
s. Few number theorists doubt that the Riemann hypothesis is true. In fact, in anticipation of its eventual proof, some have even proceeded to develop further proofs which are contingent on the truth of this conjecture. These are called '' conditional proofs'': the conjectures assumed appear in the hypotheses of the theorem, for the time being.
These "proofs", however, would fall apart if it turned out that the hypothesis was false, so there is considerable interest in verifying the truth or falsity of conjectures of this type.
In other sciences
Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is related tohypothesis
A hypothesis (plural hypotheses) is a proposed explanation for a phenomenon. For a hypothesis to be a scientific hypothesis, the scientific method requires that one can testable, test it. Scientists generally base scientific hypotheses on prev ...
, which in science
Science is a systematic endeavor that Scientific method, builds and organizes knowledge in the form of Testability, testable explanations and predictions about the universe.
Science may be as old as the human species, and some of the earli ...
refers to a testable conjecture.
See also
* Bold hypothesis *Futures studies
Futures studies, futures research, futurism or futurology is the systematic, interdisciplinary and holistic study of social and technological advancement, and other environmental trends, often for the purpose of exploring how people will l ...
* Hypotheticals
* List of conjectures
* Ramanujan machine
References
Works cited
* * *External links
*Open Problem Garden
{{Portal bar, Mathematics, Science Concepts in the philosophy of science Statements Mathematical terminology