|
Triangulation (topology)
In mathematics, triangulation describes the replacement of topological spaces with simplicial complexes by the choice of an appropriate homeomorphism. A space that admits such a homeomorphism is called a triangulable space. Triangulations can also be used to define a piecewise linear structure for a space, if one exists. Triangulation has various applications both in and outside of mathematics, for instance in algebraic topology, in complex analysis, and in modeling. Motivation On the one hand, it is sometimes useful to forget about superfluous information of topological spaces: The replacement of the original spaces with simplicial complexes may help to recognize crucial properties and to gain a better understanding of the considered object. On the other hand, simplicial complexes are objects of combinatorial character and therefore one can assign them quantities arising from their combinatorial pattern, for instance, the Euler characteristic. Triangulation allows now to as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star (simplicial Complex)
The link in a simplicial complex is a generalization of the neighborhood of a vertex in a graph. The link of a vertex encodes information about the local structure of the complex at the vertex. Link of a vertex Given an abstract simplicial complex and v a vertex in V(X), its link \operatorname(v,X) is a set containing every face \tau \in X such that v\not\in \tau and \tau\cup \ is a face of . * In the special case in which is a 1-dimensional complex (that is: a graph), \operatorname(v,X) contains all vertices u\neq v such that \ is an edge in the graph; that is, \operatorname(v, X)=\mathcal(v)=the neighborhood system of v in the graph. Given a geometric simplicial complex and v\in V(X), its link \operatorname(v,X) is a set containing every face \tau \in X such that v\not\in \tau and there is a simplex in X that has v as a vertex and \tau as a face. Equivalently, the join v \star \tau is a face in X. * As an example, suppose v is the top vertex of the tetrahedron at t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betti Number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicial complexes or CW complexes), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite. The ''n''th Betti number represents the rank of the ''n''th homology group, denoted ''H''''n'', which tells us the maximum number of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc. For example, if H_n(X) \cong 0 then b_n(X) = 0, if H_n(X) \cong \mathbb then b_n(X) = 1, if H_n(X) \cong \mathbb \oplus \mathbb then b_n(X) = 2, if H_n(X) \cong \mathbb \oplus \mathbb\oplus \mathbb then b_n(X) = 3, etc. Note that only the ranks of infinite groups are considered, so for example if H_n(X) \cong \mathbb^k \oplus \mathbb/(2), where \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finitely Generated Abelian Group
In abstract algebra, an abelian group (G,+) is called finitely generated if there exist finitely many elements x_1,\dots,x_s in G such that every x in G can be written in the form x = n_1x_1 + n_2x_2 + \cdots + n_sx_s for some integers n_1,\dots, n_s. In this case, we say that the set \ is a ''generating set'' of G or that x_1,\dots, x_s ''generate'' G. So, finitely generated abelian groups can be thought of as a generalization of cyclic groups. Every finite abelian group is finitely generated. The finitely generated abelian groups can be completely classified. Examples * The integers, \left(\mathbb,+\right), are a finitely generated abelian group. * The integers modulo n, \left(\mathbb/n\mathbb,+\right), are a finite (hence finitely generated) abelian group. * Any direct sum of finitely many finitely generated abelian groups is again a finitely generated abelian group. * Every lattice forms a finitely generated free abelian group. There are no other examples (up to isomorphism) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplicial Homology
In algebraic topology, simplicial homology is the sequence of homology groups of a simplicial complex. It formalizes the idea of the number of holes of a given dimension in the complex. This generalizes the number of connected component (topology), connected components (the case of dimension 0). Simplicial homology arose as a way to study topological spaces whose building blocks are ''n''-simplices, the ''n''-dimensional analogs of triangles. This includes a point (0-simplex), a line segment (1-simplex), a triangle (2-simplex) and a tetrahedron (3-simplex). By definition, such a space is homeomorphic to a simplicial complex (more precisely, the abstract simplicial complex, geometric realization of an abstract simplicial complex). Such a homeomorphism is referred to as a ''Triangulation (topology), triangulation'' of the given space. Many topological spaces of interest can be triangulated, including every smooth manifold (Cairns and J.H.C. Whitehead, Whitehead). Simplicial homology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Complex
In mathematics, a chain complex is an algebraic structure that consists of a sequence of abelian groups (or modules) and a sequence of homomorphisms between consecutive groups such that the image of each homomorphism is contained in the kernel of the next. Associated to a chain complex is its homology, which is (loosely speaking) a measure of the failure of a chain complex to be exact. A cochain complex is similar to a chain complex, except that its homomorphisms are in the opposite direction. The homology of a cochain complex is called its cohomology. In algebraic topology, the singular chain complex of a topological space X is constructed using continuous maps from a simplex to X, and the homomorphisms of the chain complex capture how these maps restrict to the boundary of the simplex. The homology of this chain complex is called the singular homology of X, and is a commonly used invariant of a topological space. Chain complexes are studied in homological algebra, but a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Homology
In algebraic topology, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n(X). Intuitively, singular homology counts, for each dimension n, the n-dimensional holes of a space. Singular homology is a particular example of a homology theory, which has now grown to be a rather broad collection of theories. Of the various theories, it is perhaps one of the simpler ones to understand, being built on fairly concrete constructions (see also the related theory simplicial homology). In brief, singular homology is constructed by taking maps of the simplex, standard -simplex to a topological space, and composing them into Free abelian group#Integer functions and formal sums, formal sums, called singular chains. The boundary operation – mapping each n-dimensional simplex to its (n-1)-dimensional boundary operator, boundary – induces the singular chain complex. The singular homology is then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, parallel lines) that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus ''any'' two distinct lines in a projective plane intersect at exactly one point. Renaissance artists, in developing the techniques of drawing in Perspective (graphical)#Renaissance, perspective, laid the groundwork for this mathematical topic. The archetypical example is the real projective plane, also known as the extended Euclidean plane. This example, in slightly different guises, is important in algebraic geometry, topology and projective geometry where it may be denoted variously by , RP2, or P2(R), among other notations. There are many other projective planes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
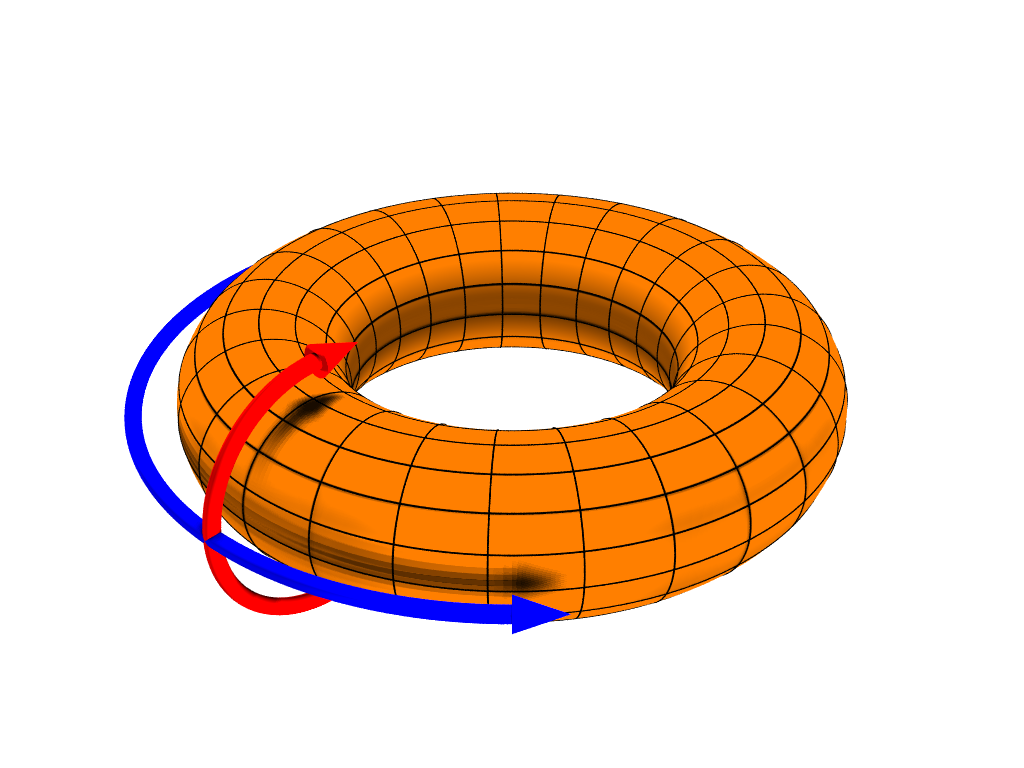
Torus Paths2
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |