|
Trirectangular Spherical Triangle
In geometry, an octant of a sphere is a spherical triangle with three right angles and three right sides. It is sometimes called a trirectangular (spherical) triangle. It is one face of a spherical octahedron. For a sphere embedded in three-dimensional Euclidean space, the vectors from the sphere's center to each vertex of an octant are the basis vectors of a Cartesian coordinate system relative to which the sphere is a unit sphere. The spherical octant itself is the intersection of the sphere with one octant of space. Uniquely among spherical triangles, the octant is its own polar triangle. The octant can be parametrized using a rational quartic Bézier triangle. The solid angle subtended by a spherical octant is /2 steradian or one-eight of a spat, the solid angle of a full sphere. See also * Trirectangular tetrahedron In geometry, a trirectangular tetrahedron is a tetrahedron where all three face angles at one vertex are right angles. That vertex is called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spat (angular Unit)
The spat (symbol sp), from the Latin ''spatium'' ("space"), is a unit of solid angle. 1 spat is equal to 4 steradians or approximately square degrees of solid angle . Thus it is the solid angle subtended by a complete sphere at its center. The whole sphere contains ~148.510 million square arcminutes and ~534.638 billion square arcseconds. See also * Turn (angle) — the plane angle counterpart of the spat, equivalent to 2 radian The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...s References Units of solid angle {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steradian
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to '' subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a ''steradian'' (symbol: sr), which is equal to one square radian, sr = rad2. One steradian corresponds to one unit of area (of any shape) on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
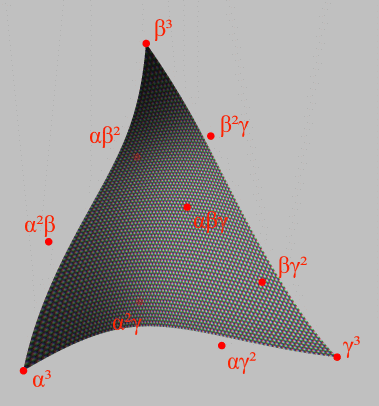
Bézier Triangle
A Bézier triangle is a special type of Bézier surface that is created by (Linearity, linear, Square (algebra), quadratic, Cube (algebra), cubic or higher degree) interpolation of control points. ''n''th-order Bézier triangle A general ''n''th-order Bézier triangle has (''n'' +1)(''n'' + 2)/2 Control point (mathematics), control points ''α''''i''''β''''j''''γ''''k'' where ''i'', ''j'', ''k'' are non-negative integers such that ''i'' + ''j'' + ''k'' = ''n''. The surface is then defined as : (\alpha s + \beta t + \gamma u)^n = \sum_ s^i t^j u^k \alpha^i \beta^j \gamma^k = \sum_ \frac s^i t^j u^k \alpha^i \beta^j \gamma^k for all non-negative real numbers ''s'' + ''t'' + ''u'' = 1. With Linearity, linear order (n=1), the resulting Bézier triangle is actually a regular flat triangle, with the triangle vertices equaling the three control points. A Square (algebra), quadratic (n=2) Bézier tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |