Bézier Triangle on:
[Wikipedia]
[Google]
[Amazon]
A Bézier triangle is a special type of Bézier surface that is created by ( linear,
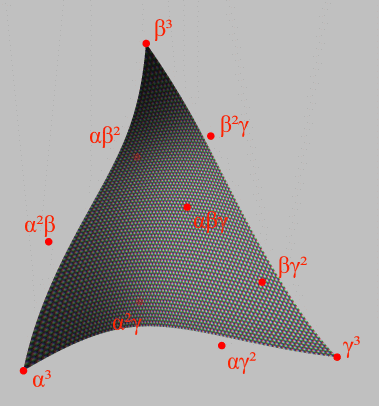 A cubic Bézier triangle is a surface with the equation
:
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and ''s'', ''t'', ''u'' (with 0 ≤ ''s'', ''t'', ''u'' ≤ 1 and ''s'' + ''t'' + ''u'' = 1) are the barycentric coordinates inside the triangle.
Alternatively, a cubic Bézier triangle can be expressed as a more generalized formulation as
:
in accordance with the formulation of the .
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves
A cubic Bézier triangle is a surface with the equation
:
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and ''s'', ''t'', ''u'' (with 0 ≤ ''s'', ''t'', ''u'' ≤ 1 and ''s'' + ''t'' + ''u'' = 1) are the barycentric coordinates inside the triangle.
Alternatively, a cubic Bézier triangle can be expressed as a more generalized formulation as
:
in accordance with the formulation of the .
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves
Quadratic Bézier Triangles As Drawing Primitives
Contains more info on planar and quadratic Bézier triangles.
Paper about the use of cubic Bézier patches in raytracing (German)
* *
Curved PN triangles (a special kind of cubic Bézier triangles)
Shape aware normal interpolation for curved surface shading from polyhedral approximation
Pixel-Shader-Based Curved Triangles
* {{DEFAULTSORT:Bezier Triangle Surfaces Multivariate interpolation
quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms. ''Quadratus'' is Latin for ''square''.
Mathematics ...
, cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
or higher degree) interpolation of control points.
''n''th-order Bézier triangle
A general ''n''th-order Bézier triangle has (''n'' +1)(''n'' + 2)/2 control points ''α''''i''''β''''j''''γ''''k'' where ''i'', ''j'', ''k'' are non-negative integers such that ''i'' + ''j'' + ''k'' = ''n''. The surface is then defined as : for all non-negative real numbers ''s'' + ''t'' + ''u'' = 1. With linear order (), the resulting Bézier triangle is actually a regular flat triangle, with the triangle vertices equaling the three control points. Aquadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms. ''Quadratus'' is Latin for ''square''.
Mathematics ...
() Bézier triangle features 6 control points which are all located on the edges. The cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
() Bézier triangle is defined by 10 control points and is the lowest order Bézier triangle that has an internal control point, not located on the edges. In all cases, the edges of the triangle will be Bézier curves of the same degree.
Cubic Bézier triangle
 A cubic Bézier triangle is a surface with the equation
:
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and ''s'', ''t'', ''u'' (with 0 ≤ ''s'', ''t'', ''u'' ≤ 1 and ''s'' + ''t'' + ''u'' = 1) are the barycentric coordinates inside the triangle.
Alternatively, a cubic Bézier triangle can be expressed as a more generalized formulation as
:
in accordance with the formulation of the .
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves
A cubic Bézier triangle is a surface with the equation
:
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and ''s'', ''t'', ''u'' (with 0 ≤ ''s'', ''t'', ''u'' ≤ 1 and ''s'' + ''t'' + ''u'' = 1) are the barycentric coordinates inside the triangle.
Alternatively, a cubic Bézier triangle can be expressed as a more generalized formulation as
:
in accordance with the formulation of the .
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves Bézier curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape t ...
s, with the same control points as the Bézier triangle.
By removing the γ''u'' term, a regular Bézier curve results. Also, while not very useful for display on a physical computer screen, by adding extra terms, a Bézier tetrahedron or Bézier polytope results.
Due to the nature of the equation, the entire triangle will be contained within the volume surrounded by the control points, and affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More generally, ...
s of the control points will correctly transform the whole triangle in the same way.
Halving a cubic Bézier triangle
An advantage of Bézier triangles in computer graphics is that dividing the Bézier triangle into two separate Bézier triangles requires only addition and division by two, rather than floating point arithmetic. This means that while Bézier triangles are smooth, they can easily be approximated using regular triangles by recursively dividing the triangle in two until the resulting triangles are considered sufficiently small. The following computes the new control points for the half of the full Bézier triangle with the corner α3, a corner halfway along the Bézier curve between α3 and β3, and the third corner γ3. : :equivalently, using addition and division by two only, : :where := means to replace the vector on the left with the vector on the right. :Note that halving a Bézier triangle is similar to halving Bézier curves of all orders up to the order of the Bézier triangle.See also
*Bézier curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape t ...
* Bézier surface (biquadratic patches are Bézier rectangles)
* Surface
References
External links
Quadratic Bézier Triangles As Drawing Primitives
Contains more info on planar and quadratic Bézier triangles.
Paper about the use of cubic Bézier patches in raytracing (German)
* *
Curved PN triangles (a special kind of cubic Bézier triangles)
Shape aware normal interpolation for curved surface shading from polyhedral approximation
Pixel-Shader-Based Curved Triangles
* {{DEFAULTSORT:Bezier Triangle Surfaces Multivariate interpolation