|
Toric Sections
Toric may refer to: Mathematics *relating to a torus ** Toric code ** Toric hyperkahler manifold ** Toric ideal ** Toric joint ** Toric manifold ** Toric orbifold ** Toric section ** Toric variety Other uses * Toric lens, a type of optical lens * Torić, a village in Bosnia and Herzegovina * Toric Robinson (born 1986), Jamaican footballer See also * Thoric, related to, or containing thorium {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
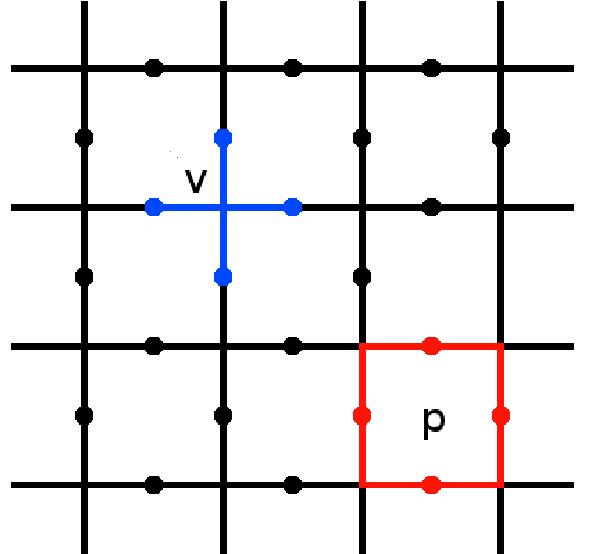
Toric Code
The toric code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two-dimensional spin lattice. It is the simplest and most well studied of the quantum double models. It is also the simplest example of topological order—''Z''2 topological order (first studied in the context of ''Z''2 spin liquid in 1991). The toric code can also be considered to be a ''Z''2 lattice gauge theory in a particular limit. It was introduced by Alexei Kitaev. The toric code gets its name from its periodic boundary conditions, giving it the shape of a torus. These conditions give the model translational invariance, which is useful for analytic study. However, some experimental realizations require open boundary conditions, allowing the system to be embedded on a 2D surface. The resulting code is typically known as the planar code. This has identical behaviour to the toric code in most, but not all, cases. Error correction and computation The toric co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Hyperkahler Manifold
In mathematics, a hypertoric variety or toric hyperkähler variety is a quaternionic analog of a toric variety In algebraic geometry, a toric variety or torus embedding is an algebraic variety containing an algebraic torus as an open dense subset, such that the action of the torus on itself extends to the whole variety. Some authors also require it to be ... constructed by applying the hyper-Kähler quotient construction of to a torus acting on a quaternionic vector space. gave a systematic description of hypertoric varieties. References * *{{citation, mr=0877637 , last1=Hitchin, first1= N. J., last2= Karlhede, first2= A., last3= Lindström, first3= U., last4= Roček, first4= M. , title=Hyper-Kähler metrics and supersymmetry , journal=Communications in Mathematical Physics, volume= 108 , year=1987, issue= 4, pages= 535–589, doi=10.1007/BF01214418, s2cid=120041594 , url=http://projecteuclid.org/euclid.cmp/1104116624 Algebraic geometry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Ideal
In algebra, a toric ideal is an ideal generated by differences of two monomials. An affine or projective algebraic variety defined by a toric prime ideal or a homogeneous toric ideal is an affine or projective toric variety In algebraic geometry, a toric variety or torus embedding is an algebraic variety containing an algebraic torus as an open dense subset, such that the action of the torus on itself extends to the whole variety. Some authors also require it to be .... References Polynomials Commutative algebra Ideals (ring theory) {{algebra-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Joint
An O-ring, also known as a packing or a toric joint, is a mechanical gasket in the shape of a torus; it is a loop of elastomer with a round cross-section, designed to be seated in a groove and compressed during assembly between two or more parts, forming a seal at the interface. The O-ring may be used in static applications or in dynamic applications where there is relative motion between the parts and the O-ring. Dynamic examples include rotating pump shafts and hydraulic cylinder pistons. Static applications of O-rings may include fluid or gas sealing applications in which: (1) the O-ring is compressed resulting in zero clearance, (2) the O-ring material is vulcanized solid such that it is impermeable to the fluid or gas, and (3) the O-ring material is resistant to degradation by the fluid or gas. The wide range of potential liquids and gases that need to be sealed has necessitated the development of a wide range of O-ring materials. O-rings are one of the most common seals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Manifold
In mathematics, a toric manifold is a topological analogue of toric variety in algebraic geometry. It is an even-dimensional manifold with an effective smooth action of an n-dimensional compact torus which is locally standard with the orbit space a simple convex polytope.. The aim is to do combinatorics on the quotient polytope and obtain information on the manifold above. For example, the Euler characteristic and the cohomology ring of the manifold can be described in terms of the polytope. The Atiyah and Guillemin- Sternberg theorem This theorem states that the image of the moment map In mathematics, specifically in symplectic geometry, the momentum map (or, by false etymology, moment map) is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. ... of a Hamiltonian toric action is the convex hull of the set of moments of the points fixed by the action. In particular, this image is a convex pol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Orbifold
In algebraic geometry, a toric stack is a stacky generalization of a toric variety. More precisely, a toric stack is obtained by replacing in the construction of a toric variety a step of taking GIT quotients with that of taking quotient stacks. Consequently, a toric variety is a coarse approximation of a toric stack. A toric orbifold is an example of a toric stack. See also *Stanley–Reisner ring In mathematics, a Stanley–Reisner ring, or face ring, is a quotient of a polynomial ring, polynomial algebra over a field (algebra), field by a square-free monomial ideal, monomial ideal (ring theory), ideal. Such ideals are described more geomet ... References * * * Algebraic geometry {{algebraic-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Section
A toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone. Special cases have been known since antiquity, and the general case was studied by Jean Gaston Darboux.. Mathematical formulae In general, toric sections are fourth-order ( quartic) plane curves of the form : \left( x^2 + y^2 \right)^2 + a x^2 + b y^2 + cx + dy + e = 0. Spiric sections A special case of a toric section is the spiric section, in which the intersecting plane is parallel to the rotational symmetry axis of the torus. They were discovered by the ancient Greek geometer Perseus in roughly 150 BC. Well-known examples include the hippopede and the Cassini oval and their relatives, such as the lemniscate of Bernoulli. Villarceau circles Another special case is the Villarceau circles, in which the intersection is a circle despite the lack of any of the obvious sorts of symmetry that would entail a circular cross-section.. General toric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Variety
In algebraic geometry, a toric variety or torus embedding is an algebraic variety containing an algebraic torus as an open dense subset, such that the action of the torus on itself extends to the whole variety. Some authors also require it to be normal. Toric varieties form an important and rich class of examples in algebraic geometry, which often provide a testing ground for theorems. The geometry of a toric variety is fully determined by the combinatorics of its associated fan, which often makes computations far more tractable. For a certain special, but still quite general class of toric varieties, this information is also encoded in a polytope, which creates a powerful connection of the subject with convex geometry. Familiar examples of toric varieties are affine space, projective spaces, products of projective spaces and bundles over projective space. Toric varieties from tori The original motivation to study toric varieties was to study torus embeddings. Given the algebr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Lens
A toric lens is a lens with different optical power and focal length in two orientations perpendicular to each other. One of the lens surfaces is shaped like a "cap" from a torus (see figure at right), and the other one is usually spherical. Such a lens behaves like a combination of a spherical lens and a cylindrical lens. Toric lenses are used primarily in eyeglasses, contact lenses and intraocular lenses to correct astigmatism. Torus A torus is the surface of revolution resulting when a circle with radius ''r'' rotates around an axis lying within the same plane as the circle, at a distance ''R'' from the circle's centre (see figure at right). If ''R'' > ''r'', a ''ring torus'' is produced. If ''R'' = ''r'', a ''horn torus'' is produced, where the opening is contracted into a single point. ''R'' < ''r'' results in a ''spindle torus'', where only two "dips" remain from the opening; these dips become less deep as ''R'' approaches 0. When ''R''&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torić
Torič ( sr-cyrl, Торич) is a village in the municipality of Bileća, Republika Srpska, Bosnia and Herzegovina Bosnia and Herzegovina, sometimes known as Bosnia-Herzegovina and informally as Bosnia, is a country in Southeast Europe. Situated on the Balkans, Balkan Peninsula, it borders Serbia to the east, Montenegro to the southeast, and Croatia to th ....Official results from the book: Ethnic composition of Bosnia-Herzegovina population, by municipalities and settlements, 1991. census, Zavod za statistiku Bosne i Hercegovine - Bilten no.234, Sarajevo 1991. References Villages in Republika Srpska Populated places in Bileća {{Bileća-geo-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Robinson
Toric Robinson (born 6 February 1986) is a Jamaican association football, footballer currently playing for Antigua Barracuda FC in the USL Professional Division. References External links Info Sport profile 1986 births Living people Jamaican men's footballers 21st-century Jamaican sportsmen Jamaican expatriate men's footballers East Stroudsburg Warriors men's soccer players Jersey Express S.C. players Dayton Dutch Lions players Antigua Barracuda FC players Expatriate men's soccer players in the United States Expatriate men's footballers in Antigua and Barbuda USL League Two players USL Championship players Jamaican expatriate sportspeople in Antigua and Barbuda Jamaican expatriate sportspeople in the United States Men's association football midfielders Sportspeople from Westmoreland Parish {{Jamaica-footy-bio-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |