|
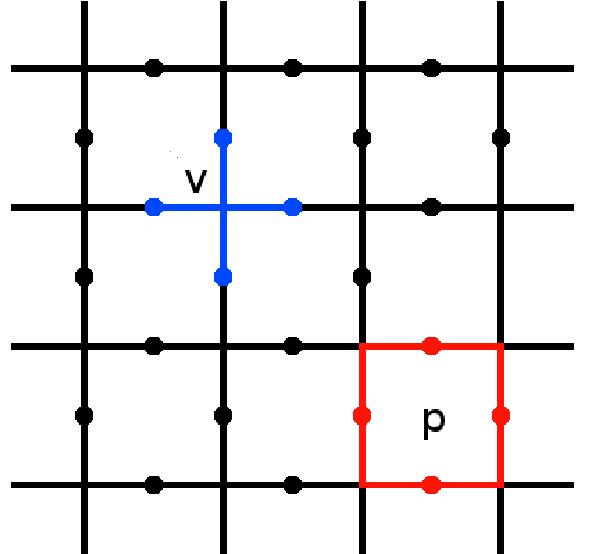
Toric Code
The toric code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two-dimensional spin lattice. It is the simplest and most well studied of the quantum double models. It is also the simplest example of topological order—''Z''2 topological order (first studied in the context of ''Z''2 spin liquid in 1991). The toric code can also be considered to be a ''Z''2 lattice gauge theory in a particular limit. It was introduced by Alexei Kitaev. The toric code gets its name from its periodic boundary conditions, giving it the shape of a torus. These conditions give the model translational invariance, which is useful for analytic study. However, some experimental realizations require open boundary conditions, allowing the system to be embedded on a 2D surface. The resulting code is typically known as the planar code. This has identical behaviour to the toric code in most, but not all, cases. Error correction and computation The toric co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Order
In physics, topological order describes a state or phase of matter that arises system with non-local interactions, such as entanglement in quantum mechanics, and floppy modes in elastic systems. Whereas classical phases of matter such as gases and solids correspond to microscopic patterns in the spatial arrangement of particles arising from short range interactions, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders (or different patterns of long range entanglements) cannot change into each other without a phase transition. Technically, topological order occurs at zero temperature. Various topologically ordered states have interesting properties, such as (1) ground state degeneracy and fractional statistics or non-abelian group statistics that can be used to realize a topological quantum computer; (2) perfect conducting edge states that may have important device applications; (3) emergent gauge field and Fermi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiparticles
In condensed matter physics, a quasiparticle is a concept used to describe a collective behavior of a group of particles that can be treated as if they were a single particle. Formally, quasiparticles and collective excitations are closely related phenomena that arise when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in vacuum. For example, as an electron travels through a semiconductor, its motion is disturbed in a complex way by its interactions with other electrons and with atomic nuclei. The electron behaves as though it has a different effective mass travelling unperturbed in vacuum. Such an electron is called an ''electron quasiparticle''. In another example, the aggregate motion of electrons in the valence band of a semiconductor or a hole band in a metal behave as though the material instead contained positively charged quasiparticles called ''electron holes''. Other quasiparticles or collective ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Entanglement Entropy
The topological entanglement entropy or ''topological entropy'', usually denoted by \gamma, is a number characterizing many-body states that possess topological order. A non-zero topological entanglement entropy reflects the presence of long range quantum entanglements in a many-body quantum state. So the topological entanglement entropy links topological order with pattern of long range quantum entanglements. Given a topologically ordered state, the topological entropy can be extracted from the asymptotic behavior of the Von Neumann entropy measuring the quantum entanglement between a spatial block and the rest of the system. The entanglement entropy of a simply connected region of boundary length ''L'', within an infinite two-dimensional topologically ordered state, has the following form for large ''L'': : S_L \; \longrightarrow \; \alpha L -\gamma +\mathcal(L^) \; , \qquad \nu>0 \,\! where -\gamma is the topological entanglement entropy. The topological entanglement en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String-net Liquid
In condensed matter physics, a string-net is an extended object whose collective behavior has been proposed as a physical mechanism for topological order by Michael A. Levin and Xiao-Gang Wen. A particular string-net model may involve only closed loops; or networks of oriented, labeled strings obeying branching rules given by some gauge group; or still more general networks. Overview The string-net model is claimed to show the derivation of photons, electrons, and U(1) gauge charge, small (relative to the Planck mass) but nonzero masses, and suggestions that the leptons, quarks, and gluons can be modeled in the same way. In other words, string-net condensation provides a unified origin for photons and electrons (or gauge bosons and fermions). It can be viewed as an origin of light and electron (or gauge interactions and Fermi statistics). However, their model does not account for the chiral coupling between the fermions and the SU(2) gauge bosons in the standard model. F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–statistics Theorem
The spin–statistics theorem proves that the observed relationship between the intrinsic spin of a particle (angular momentum not due to the orbital motion) and the quantum particle statistics of collections of such particles is a consequence of the mathematics of quantum mechanics. According to the theorem, the many-body wave function for elementary particles with integer spin ( bosons) is symmetric under the exchange of any two particles, whereas for particles with half-integer spin ( fermions), the wave function is antisymmetric under such an exchange. A consequence of the theorem is that non-interacting particles with integer spin obey Bose–Einstein statistics, while those with half-integer spin obey Fermi–Dirac statistics. Background The statistics of indistinguishable particles is among the most fundamental of physical effects. The Pauli exclusion principle that every occupied quantum state contains at most one fermion controls the formation of matter. The basic bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermionic
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin , spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum number relation. As a cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bosonic
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-integer spin (1/2, 3/2, 5/2, ...). Every observed subatomic particle is either a boson or a fermion. Paul Dirac coined the name ''boson'' to commemorate the contribution of Satyendra Nath Bose, an Indian physicist. Some bosons are elementary particles occupying a special role in particle physics, distinct from the role of fermions (which are sometimes described as the constituents of "ordinary matter"). Certain elementary bosons (e.g. gluons) act as force carriers, which give rise to forces between other particles, while one (the Higgs boson) contributes to the phenomenon of mass. Other bosons, such as mesons, are composite particles made up of smaller constituents. Outside the realm of particle physics, multiple identical composite bosons behav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anyons
In physics, an anyon is a type of quasiparticle so far observed only in two-dimensional systems. In three-dimensional systems, only two kinds of elementary particles are seen: fermions and bosons. Anyons have statistical properties intermediate between fermions and bosons. In general, the operation of exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as ''abelian'' or ''non-abelian''. Abelian anyons, detected by two experiments in 2020, play a major role in the fractional quantum Hall effect. Introduction The statistical mechanics of large many-body systems obeys laws described by Maxwell–Boltzmann statistics. Quantum statistics is more complicated because of the different behaviors of two different kinds of particles called fermions and bosons. In two-dimensional systems, however, there is a third type of particle, called an anyon. In a two-dimensional world, two identical anyons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-way Quantum Computer
The one-way quantum computer, also known as measurement-based quantum computer (MBQC), is a method of quantum computing that first prepares an Quantum entanglement, entangled ''resource state'', usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements. The outcome of each individual measurement is random, but they are related in such a way that the computation always succeeds. In general, the choices of basis (linear algebra), basis for later measurements need to depend on the results of earlier measurements, and hence the measurements cannot all be performed at the same time. The implementation of MBQC is mainly considered for Photonics, photonic devices, due to the difficulty of entangling photons without measurements, and the simplicity of creating and measuring them. However, MBQC is also possible with matter-based qubits. The process of entanglement and measurement can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Gate
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate (or simply quantum gate) is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits. Unlike many classical logic gates, quantum logic gates are reversible computing, reversible. It is possible to perform classical computing using only reversible gates. For example, the reversible Toffoli gate can implement all Boolean functions, often at the cost of having to use ancilla bits. The Toffoli gate has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits. Quantum gates are unitary operators, and are described as unitary matrix, unitary matrices relative to some orthonormal Basis (linear algebra), basis. Usually the ''computational basis'' is used, which unless comparing it with somethin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computation
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of both particles and waves, and quantum computing takes advantage of this behavior using specialized hardware. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations exponentially faster than any modern "classical" computer. Theoretically a large-scale quantum computer could break some widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications. The basic unit of information in quantum computing, the qubit (or "quantum bit"), serves the same function as the bit in classical computing. However, unlike a classical bit, which can be in one of two states (a binary), a qubit can exist in a superposition of its two "bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmonds's Matching Algorithm
In graph theory, the blossom algorithm is an algorithm for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph , the algorithm finds a matching such that each vertex in is incident with at most one edge in and is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph. The algorithm runs in time , where is the number of edges of the graph and is its number of vertices. A better running time of O( , E, \sqrt ) for the same task can be achieved with the much more complex algorithm of Micali and Vazirani. A major reason that the blossom algorithm is important is that it gave the first proof that a maximum-size matching could be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |