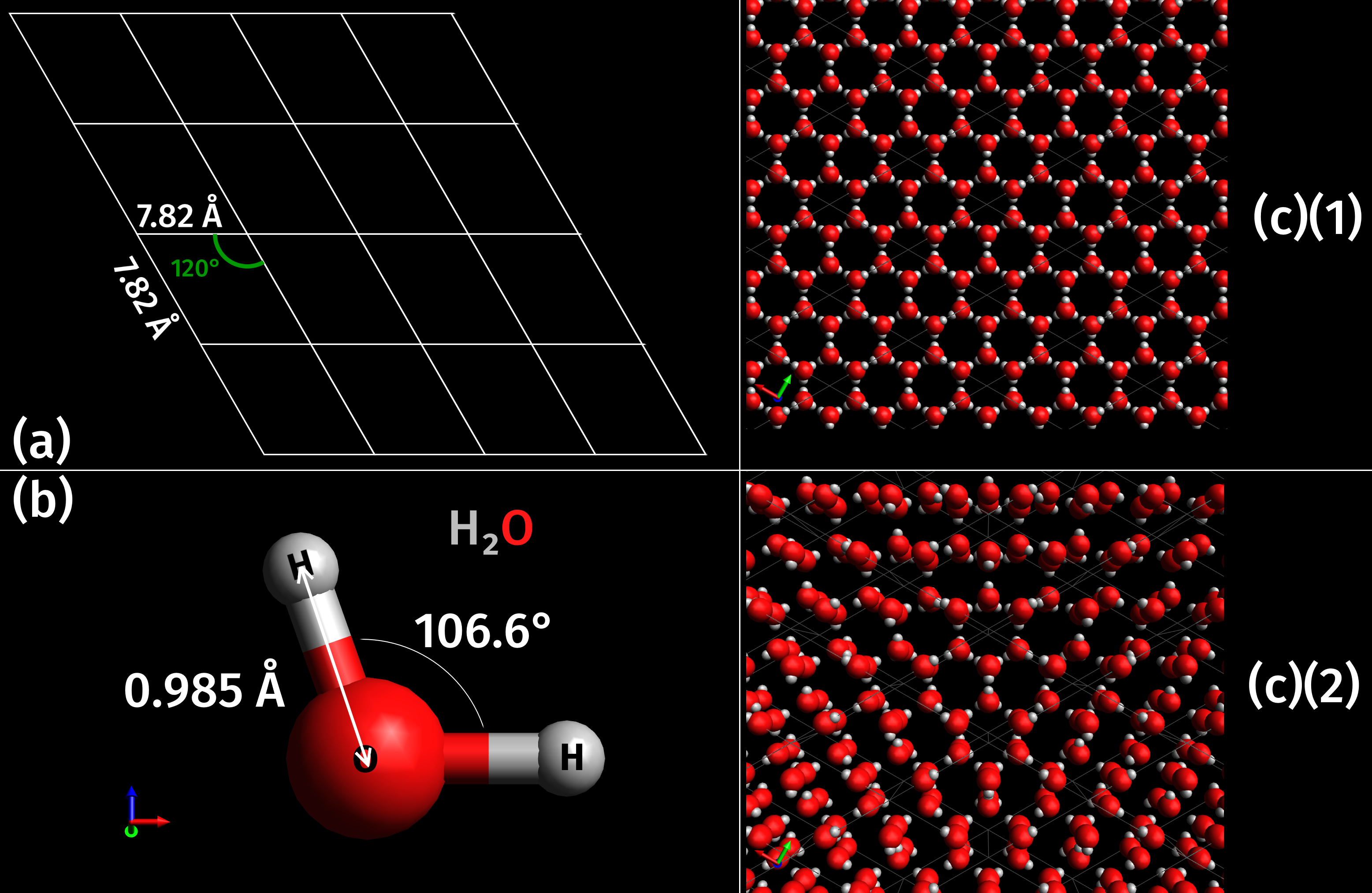
|
Sufficient Correctness
In logic and mathematics, necessity and sufficiency are terms used to describe a conditional or implicational relationship between two statements. For example, in the conditional statement: "If then ", is necessary for , because the truth of is guaranteed by the truth of . (Equivalently, it is impossible to have without , or the falsity of ensures the falsity of .) Similarly, is sufficient for , because being true always implies that is true, but not being true does not always imply that is not true. In general, a necessary condition is one (possibly one of several conditions) that must be present in order for another condition to occur, while a sufficient condition is one that produces the said condition. The assertion that a statement is a "necessary ''and'' sufficient" condition of another means that the former statement is true if and only if the latter is true. That is, the two statements must be either simultaneously true, or simultaneously false. In ordinary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contraposition
In logic and mathematics, contraposition, or ''transposition'', refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as . The contrapositive of a statement has its antecedent and consequent negated and swapped. Conditional statement P \rightarrow Q. In formulas: the contrapositive of P \rightarrow Q is \neg Q \rightarrow \neg P . If ''P'', Then ''Q''. — If not ''Q'', Then not ''P''. "If ''it is raining,'' then ''I wear my coat''." — "If ''I don't wear my coat,'' then ''it isn't raining''." The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true. Contraposition ( \neg Q \rightarrow \neg P ) can be compared with three other operations: ; Inversion (the inverse), \neg P \rightarrow \neg Q:"If ''it is not raining,'' then ''I don't wear my coat''." Unlike the contrapositive, the inverse's truth value is not at all dependen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous non-classical treatments, motivated by problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Playing Card
A playing card is a piece of specially prepared card stock, heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic that is marked with distinguishing motifs. Often the front (face) and back of each card has a finish to make handling easier. They are most commonly used for playing card games, and are also used in magic tricks, cardistry, card throwing, and card houses; cards may also be collected. Playing cards are typically palm-sized for convenient handling, and usually are sold together in a set as a deck of cards or pack of cards. The most common type of playing card in the West is the French-suited, standard 52-card pack, of which the most widespread design is the English pattern, followed by the Belgian-Genoese pattern. However, many countries use other, traditional types of playing card, including those that are German, Italian, Spanish and Swiss-suited. Tarot cards (also known locally as ''Tarocks'' or ''tarocchi'') are an ol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Veto Override
A veto is a legal power to unilaterally stop an official action. In the most typical case, a president or monarch vetoes a bill to stop it from becoming law. In many countries, veto powers are established in the country's constitution. Veto powers are also found at other levels of government, such as in state, provincial or local government, and in international bodies. Some vetoes can be overcome, often by a supermajority vote: in the United States, a two-thirds vote of the House and Senate can override a presidential veto. Article I, Section 7, Clause 2 of the United States Constitution Some vetoes, however, are absolute and cannot be overridden. For example, in the United Nations Security Council, the five permanent members (China, France, Russia, the United Kingdom, and the United States) have an absolute veto over any Security Council resolution. In many cases, the veto power can only be used to prevent changes to the status quo. But some veto powers also include the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Veto
A veto is a legal power to unilaterally stop an official action. In the most typical case, a president (government title), president or monarch vetoes a bill (law), bill to stop it from becoming statutory law, law. In many countries, veto powers are established in the country's constitution. Veto powers are also found at other levels of government, such as in state, provincial or local government, and in international bodies. Some vetoes can be overcome, often by a supermajority vote: Veto power in the United States, in the United States, a two-thirds vote of the United States House of Representatives, House and United States Senate, Senate can override a presidential veto.Article One of the United States Constitution#Clause 2: From bills to law, Article I, Section 7, Clause 2 of the United States Constitution Some vetoes, however, are absolute and cannot be overridden. For example, United Nations Security Council veto power, in the United Nations Security Council, the five per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ICE 3 Fahlenbach
Ice is water that is frozen into a solid state, typically forming at or below temperatures of 0 ° C, 32 ° F, or 273.15 K. It occurs naturally on Earth, on other planets, in Oort cloud objects, and as interstellar ice. As a naturally occurring crystalline inorganic solid with an ordered structure, ice is considered to be a mineral. Depending on the presence of impurities such as particles of soil or bubbles of air, it can appear transparent or a more or less opaque bluish-white color. Virtually all of the ice on Earth is of a hexagonal crystalline structure denoted as ''ice Ih'' (spoken as "ice one h"). Depending on temperature and pressure, at least nineteen phases ( packing geometries) can exist. The most common phase transition to ice Ih occurs when liquid water is cooled below (, ) at standard atmospheric pressure. When water is cooled rapidly (quenching), up to three types of amorphous ice can form. Interstellar ice is overwhelmingly low-density amorphous ice (L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjunction (logic)
In logic, mathematics and linguistics, ''and'' (\wedge) is the truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as \wedge or \& or K (prefix) or \times or \cdot in which \wedge is the most modern and widely used. The ''and'' of a set of operands is true if and only if ''all'' of its operands are true, i.e., A \land B is true if and only if A is true and B is true. An operand of a conjunction is a conjunct. Beyond logic, the term "conjunction" also refers to similar concepts in other fields: * In natural language, the denotation of expressions such as English " and"; * In programming languages, the short-circuit and control structure; * In set theory, intersection. * In lattice theory, logical conjunction ( greatest lower bound). Notation And is usually denoted by an infix operator: in mathematics and logic, it is denoted by a "wedge" \wedge (Unicode ), \& or \times; in electronics, \cdot; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associative
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs. Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations: \begin (2 + 3) + 4 &= 2 + (3 + 4) = 9 \,\\ 2 \times (3 \times 4) &= (2 \times 3) \times 4 = 24 . \end Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds true when performing addition and multiplication on any real numbers, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Operation
In mathematics, a binary operation or dyadic operation is a rule for combining two elements (called operands) to produce another element. More formally, a binary operation is an operation of arity two. More specifically, a binary operation on a set is a binary function that maps every pair of elements of the set to an element of the set. Examples include the familiar arithmetic operations like addition, subtraction, multiplication, set operations like union, complement, intersection. Other examples are readily found in different areas of mathematics, such as vector addition, matrix multiplication, and conjugation in groups. A binary function that involves several sets is sometimes also called a ''binary operation''. For example, scalar multiplication of vector spaces takes a scalar and a vector to produce a vector, and scalar product takes two vectors to produce a scalar. Binary operations are the keystone of most structures that are studied in algebra, in parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |