|
Space Group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
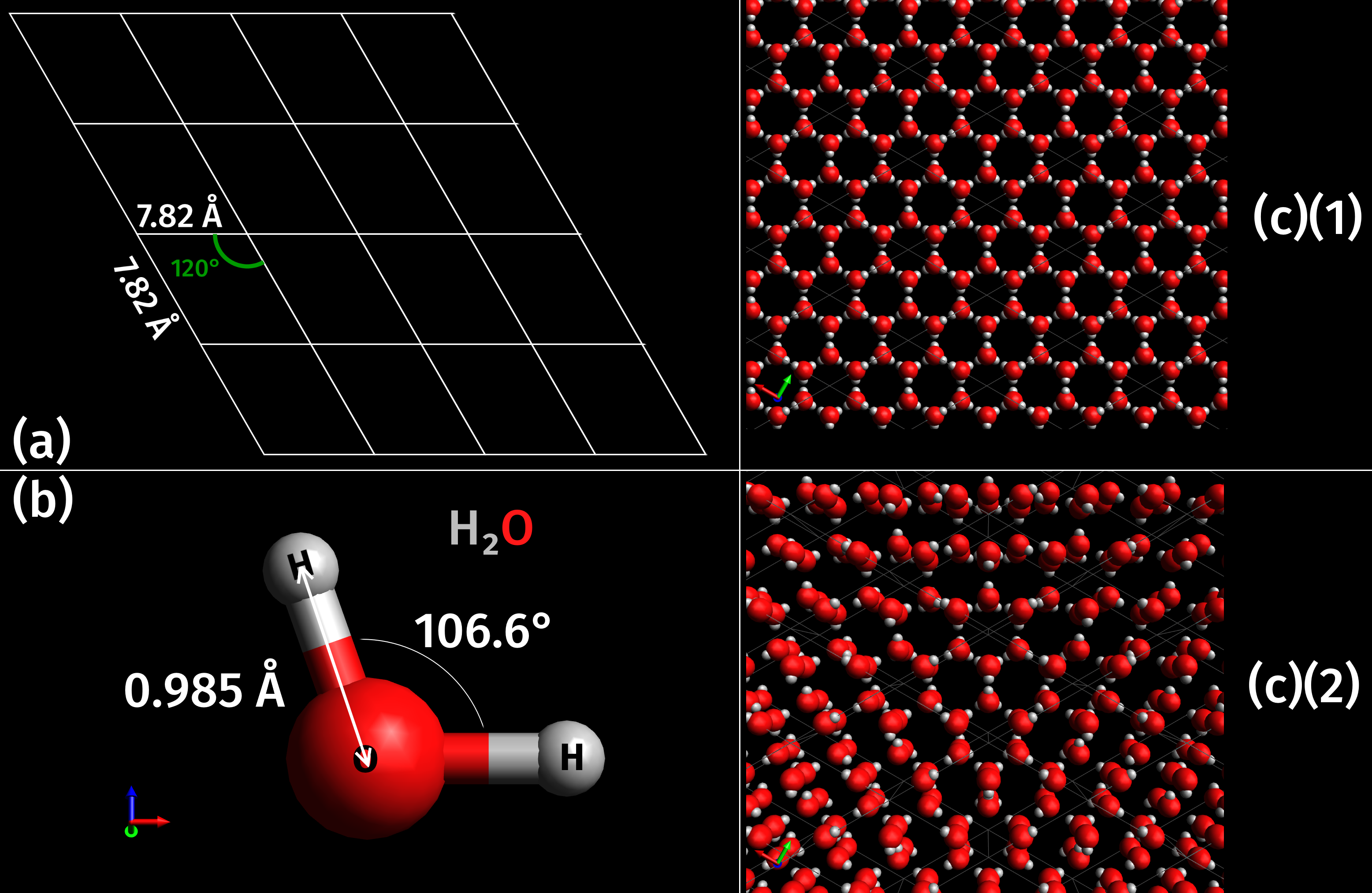
Ice Ih Space Group
Ice is water that is freezing, frozen into a solid state, typically forming at or below temperatures of 0 °Celsius, C, 32 °Fahrenheit, F, or 273.15 Kelvin, K. It occurs naturally on Earth, on other planets, in Oort cloud objects, and as interstellar ice. As a naturally occurring crystalline inorganic solid with an ordered structure, ice is considered to be a mineral. Depending on the presence of Impurity, impurities such as particles of soil or bubbles of air, it can appear transparent or a more or less Opacity (optics), opaque bluish-white color. Virtually all of the ice on Earth is of a Hexagonal crystal system, hexagonal Crystal structure, crystalline structure denoted as ''ice Ih'' (spoken as "ice one h"). Depending on temperature and pressure, at least nineteen phases of ice, phases (Sphere packing, packing geometries) can exist. The most common phase transition to ice Ih occurs when liquid water is cooled below (, ) at standard atmospheric pressure. When water is coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant under some Transformation (function), transformations, such as Translation (geometry), translation, Reflection (mathematics), reflection, Rotation (mathematics), rotation, or Scaling (geometry), scaling. Although these two meanings of the word can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a space, spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including scientific model, theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Screw Axis
A screw axis (helical axis or twist axis) is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis. Plücker coordinates are used to locate a screw axis in space, and consist of a pair of three-dimensional vectors. The first vector identifies the direction of the axis, and the second locates its position. The special case when the first vector is zero is interpreted as a pure translation in the direction of the second vector. A screw axis is associated with each pair of vectors in the algebra of screws, also known as screw theory. The spatial movement of a body can be represented by a continuous set of displacements. Because each of these displacements has a screw axis, the movement has an associated ruled surface known as a ''screw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Improper Rotation
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a Rotation (geometry), rotation about an axis and a reflection (mathematics), reflection in a plane perpendicular to that axis. Reflection and Point reflection, inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of Symmetry (geometry), geometric symmetry, molecular symmetry and Crystallographic point group, crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a ''center of rotation''. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation (between arbitrary orientation (geometry), orientations), in contrast to rotation around a fixed axis, rotation around a axis. The special case of a rotation with an internal axis passing through the body's own center of mass is known as a spin (or ''autorotation''). In that case, the surface intersection of the internal ''spin axis'' can be called a ''pole''; for example, Earth's rotation defines the geographical poles. A rotation around an axis completely external to the moving body is called a revolution (or ''orbit''), e.g. Earth's orbit around the Sun. The en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection (mathematics)
In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as the set of fixed points; this set is called the axis (in dimension 2) or plane (in dimension 3) of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis (a ''vertical reflection'') would look like q. Its image by reflection in a horizontal axis (a ''horizontal reflection'') would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state. The term ''reflection'' is sometimes used for a larger class of mappings from a Euclidean space to itself, namely the non-identity isometries that are involutions. The set of fixed points (the "mirror") of such an isome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
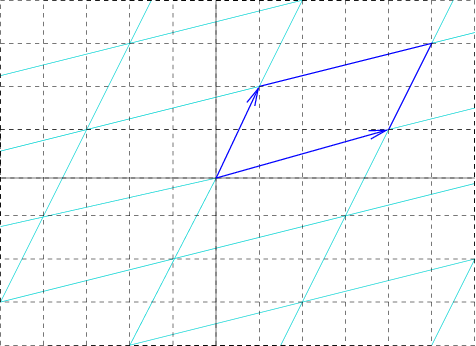
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ..., for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice System
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices (an infinite array of discrete points). Space groups (symmetry groups of a configuration in space) are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family. The seven crystal systems are ''triclinic'', ''monoclinic'', ''orthorhombic'', ''tetragonal'', ''trigonal'', ''hexagonal'', and ''cubic''. Informally, two crystals are in the same crystal system if they have similar symmetries (though there are many exceptions). Classifications Crystals can be classified in three ways: lattice systems, crystal systems and crystal families. The various classifications are often confused: in particular the trigonal crystal system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bravais Lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by : \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n_3 \mathbf_3, where the ''ni'' are any integers, and a''i'' are ''primitive translation vectors'', or ''primitive vectors'', which lie in different directions (not necessarily mutually perpendicular) and span the lattice. The choice of primitive vectors for a given Bravais lattice is not unique. A fundamental aspect of any Bravais lattice is that, for any choice of direction, the lattice appears exactly the same from each of the discrete lattice points when looking in that chosen direction. The Bravais lattice concept is used to formally define a ''crystalline arrangement'' and its (finite) frontiers. A crystal is made up of one or more atoms, called the ''basis'' or ''motif'', at each lattice point. The ''basis'' may consist of atoms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallographic Point Group
In crystallography, a crystallographic point group is a three-dimensional point group whose symmetry operations are compatible with a three-dimensional crystallographic lattice. According to the crystallographic restriction it may only contain one-, two-, three-, four- and sixfold rotations or rotoinversions. This reduces the number of crystallographic point groups to 32 (from an infinity of general point groups). These 32 groups are the same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms. In 1867 Axel Gadolin, who was unaware of the previous work of Hessel, found the crystallographic point groups independently using stereographic projection to represent the symmetry elements of the 32 groups. In the classification of crystals, to each space group is associated a crystallographic point group by "forgetting" the translational components of the symmetry operatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Moritz Schoenflies
Arthur Moritz Schoenflies (; 17 April 1853 – 27 May 1928), sometimes written as Schönflies, was a German mathematician, known for his contributions to the application of group theory to crystallography, and for work in topology. Schoenflies was born in Landsberg an der Warthe (modern Gorzów, Poland). Arthur Schoenflies married Emma Levin (1868–1939) in 1896. He studied under Ernst Kummer and Karl Weierstrass, and was influenced by Felix Klein. The Schoenflies problem is to prove that an (n - 1)-sphere in Euclidean ''n''-space bounds a topological ball, however embedded. This question is much more subtle than it initially appears. He studied at the University of Berlin from 1870 to 1875. He obtained a doctorate in 1877, and in 1878 he was a teacher at a school in Berlin. In 1880, he went to Colmar to teach. Schoenflies was a frequent contributor to Klein's ''Encyclopedia of Mathematical Sciences'': In 1898 he wrote on set theory, in 1902 on kinematics, and on proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bibliotheca Teubneriana
The Bibliotheca Teubneriana, or ''Bibliotheca Scriptorum Graecorum et Romanorum Teubneriana'', also known as Teubner editions of Greek and Latin texts, comprise one of the most thorough modern collections published of ancient (and some medieval) Greco-Roman literature. The series consists of critical editions by leading scholars. They now always come with a full critical apparatus on each page, although during the nineteenth century there were ''editiones minores'', published either without critical apparatuses or with abbreviated textual appendices, and ''editiones maiores'', published with a full apparatus. Teubneriana is an abbreviation used to denote mainly a single volume of the series (fully: ''editio Teubneriana''), rarely the whole collection; correspondingly, ''Oxoniensis'' is used with reference to the ''Scriptorum Classicorum Bibliotheca Oxoniensis'', mentioned above as ''Oxford Classical Texts''. The only comparable publishing ventures producing authoritative schol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |