screw axis on:
[Wikipedia]
[Google]
[Amazon]
 A screw axis (helical axis or twist axis) is a line that is simultaneously the
A screw axis (helical axis or twist axis) is a line that is simultaneously the
 A screw displacement (also screw operation or rotary translation) is the composition of a rotation by an angle ''φ'' about an axis (called the screw axis) with a translation by a distance ''d'' along this axis. A positive rotation direction usually means one that corresponds to the translation direction by the
A screw displacement (also screw operation or rotary translation) is the composition of a rotation by an angle ''φ'' about an axis (called the screw axis) with a translation by a distance ''d'' along this axis. A positive rotation direction usually means one that corresponds to the translation direction by the 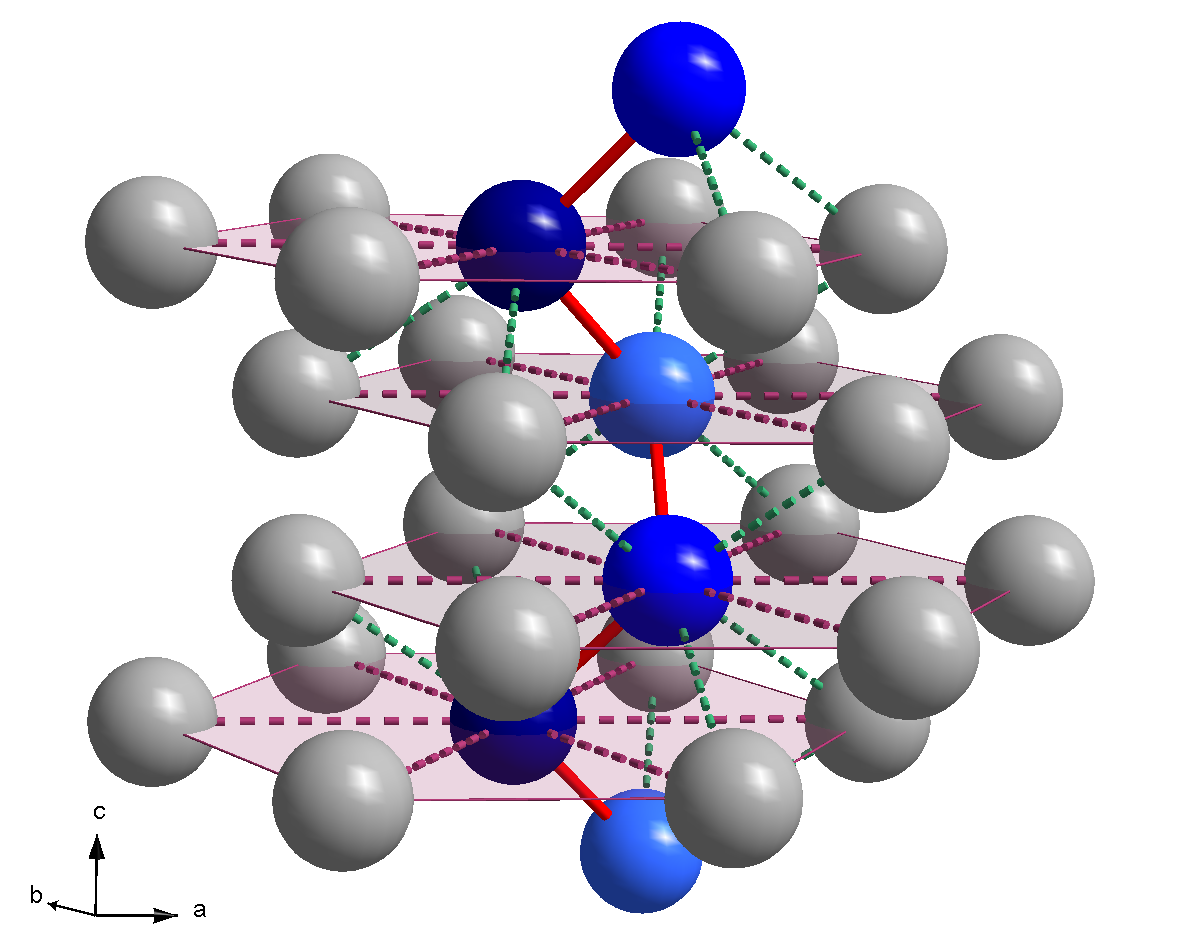 In
In
/ref> : Solve this equation for C using
axis of rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
and the line along which translation
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.
Plücker coordinates are used to locate a screw axis in space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
, and consist of a pair of three-dimensional vectors. The first vector identifies the direction of the axis, and the second locates its position. The special case when the first vector is zero is interpreted as a pure translation in the direction of the second vector. A screw axis is associated with each pair of vectors in the algebra of screws, also known as screw theory.
The spatial movement of a body can be represented by a continuous set of displacements. Because each of these displacements has a screw axis, the movement has an associated ruled surface known as a ''screw surface''. This surface is not the same as the ''axode'', which is traced by the instantaneous screw axes of the movement of a body. The instantaneous screw axis, or 'instantaneous helical axis' (IHA), is the axis of the helicoidal field generated by the velocities of every point in a moving body.
When a spatial displacement specializes to a planar displacement, the screw axis becomes the ''displacement pole'', and the instantaneous screw axis becomes the ''velocity pole'', or instantaneous center of rotation, also called an ''instant center''. The term ''centro'' is also used for a velocity pole, and the locus of these points for a planar movement is called a centrode.
History
The proof that a spatial displacement can be decomposed into a rotation around, and translation along, a line in space is attributed to Michel Chasles in 1830. Recently the work of Giulio Mozzi has been identified as presenting a similar result in 1763.Screw axis symmetry
 A screw displacement (also screw operation or rotary translation) is the composition of a rotation by an angle ''φ'' about an axis (called the screw axis) with a translation by a distance ''d'' along this axis. A positive rotation direction usually means one that corresponds to the translation direction by the
A screw displacement (also screw operation or rotary translation) is the composition of a rotation by an angle ''φ'' about an axis (called the screw axis) with a translation by a distance ''d'' along this axis. A positive rotation direction usually means one that corresponds to the translation direction by the right-hand rule
In mathematics and physics, the right-hand rule is a Convention (norm), convention and a mnemonic, utilized to define the orientation (vector space), orientation of Cartesian coordinate system, axes in three-dimensional space and to determine the ...
. This means that if the rotation is clockwise, the displacement is away from the viewer. Except for ''φ'' = 180°, we have to distinguish a screw displacement from its mirror image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it r ...
. Unlike for rotations, a righthand and lefthand screw operation generate different groups.
The combination of a rotation about an axis and a translation in a direction perpendicular to that axis is a rotation about a parallel axis. However, a screw operation with a nonzero translation vector along the axis cannot be reduced like that. Thus the effect of a rotation combined with ''any'' translation is a screw operation in the general sense, with as special cases a pure translation, a pure rotation and the identity. Together these are all the direct isometries in 3D.
 In
In crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
, a screw axis symmetry is a combination of rotation about an axis and a translation parallel to that axis which leaves a crystal unchanged. If ''φ'' = for some positive integer ''n'', then screw axis symmetry implies translational symmetry with a translation vector which is ''n'' times that of the screw displacement.
Applicable for space group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that ...
s is a rotation by about an axis, combined with a translation along the axis by a multiple of the distance of the translational symmetry, divided by ''n''. This multiple is indicated by a subscript. So, 63 is a rotation of 60° combined with a translation of one half of the lattice vector, implying that there is also 3-fold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...
about this axis. The possibilities are 21, 31, 41, 42, 61, 62, and 63, and the enantiomorphous 32, 43, 64, and 65.
Considering a screw axis ''n'', if ''g'' is the greatest common divisor
In mathematics, the greatest common divisor (GCD), also known as greatest common factor (GCF), of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers , , the greatest co ...
of ''n'' and ''m'', then there is also a ''g''-fold rotation axis. When screw operations have been performed, the displacement will be , which since it is a whole number means one has moved to an equivalent point in the lattice, while carrying out a rotation by . So 4, 6 and 6 create two-fold rotation axes, while 6 creates a three-fold axis.
A non-discrete screw axis isometry group
In mathematics, the isometry group of a metric space is the set of all bijective isometries (that is, bijective, distance-preserving maps) from the metric space onto itself, with the function composition as group operation. Its identity element ...
contains all combinations of a rotation about some axis and a proportional translation along the axis (in rifling
Rifling is the term for helical grooves machined into the internal surface of a firearms's barrel for imparting a spin to a projectile to improve its aerodynamic stability and accuracy. It is also the term (as a verb) for creating such groov ...
, the constant of proportionality is called the twist rate); in general this is combined with ''k''-fold rotational isometries about the same axis (''k'' ≥ 1); the set of images of a point under the isometries is a ''k''-fold helix; in addition there may be a 2-fold rotation about a perpendicularly intersecting axis, and hence a ''k''-fold helix of such axes.
Screw axis of a spatial displacement
Geometric argument
Let be an orientation-preserving rigid motion of R3. The set of these transformations is a subgroup of Euclidean motions known as the special Euclidean group SE(3). These rigid motions are defined by transformations of x in R3 given by : consisting of a three-dimensional rotation ''A'' followed by a translation by the vector d. A three-dimensionalrotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
''A'' has a unique axis that defines a line ''L''. Let the unit vector along this line be S so that the translation vector d can be resolved into a sum of two vectors, one parallel and one perpendicular to the axis ''L'', that is,
:
In this case, the rigid motion takes the form
:
Now, the orientation preserving rigid motion ''D''* = ''A''(x) + d⊥ transforms all the points of R3 so that they remain in planes perpendicular to ''L''. For a rigid motion of this type there is a unique point c in the plane ''P'' perpendicular to ''L'' through 0, such that
:
The point C can be calculated as
:
because d⊥ does not have a component in the direction of the axis of ''A''.
A rigid motion ''D''* with a fixed point must be a rotation of around the axis ''L''c through the point c. Therefore, the rigid motion
:
consists of a rotation about the line ''L''c followed by a translation by the vector d''L'' in the direction of the line ''L''c.
Conclusion: every rigid motion of R3 is the result of a rotation of R3 about a line ''L''c followed by a translation in the direction of the line. The combination of a rotation about a line and translation along the line is called a screw motion.
Computing a point on the screw axis
A point C on the screw axis satisfies the equation:J. M. McCarthy and G. S. Soh, ''Geometric Design of Linkages'', 2nd Edition, Springer 2010/ref> : Solve this equation for C using
Cayley's formula
In mathematics, Cayley's formula is a result in graph theory named after Arthur Cayley. It states that for every positive integer n, the number of trees on n labeled vertices is n^.
The formula equivalently counts the spanning trees of a ...
for a rotation matrix
:
where is the skew-symmetric matrix constructed from Rodrigues' vector
:
such that
:
Use this form of the rotation ''A'' to obtain
:
which becomes
:
This equation can be solved for C on the screw axis P(t) to obtain,
:
The screw axis of this spatial displacement has the Plücker coordinates .
Dual quaternion
The screw axis appears in the dual quaternion formulation of a spatial displacement . The dual quaternion is constructed from the dual vector defining the screw axis and the dual angle , where ''φ'' is the rotation about and ''d'' the slide along this axis, which defines the displacement D to obtain, : A spatial displacement of points q represented as a vector quaternion can be defined usingquaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s as the mapping
:
where d is translation vector quaternion and ''S'' is a unit quaternion, also called a versor
In mathematics, a versor is a quaternion of Quaternion#Norm, norm one, also known as a unit quaternion. Each versor has the form
:u = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi
where the r2 = −1 conditi ...
, given by
:
that defines a rotation by 2''θ'' around an axis S.
In the proper Euclidean group
In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space \mathbb^n; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformati ...
E+(3) a rotation may be conjugated with a translation to move it to a parallel rotation axis. Such a conjugation, using quaternion homographies, produces the appropriate screw axis to express the given spatial displacement as a screw displacement, in accord with Chasles’ theorem.
Mechanics
The instantaneous motion of arigid body
In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body rema ...
may be the combination of rotation about an axis (the screw axis) and a translation along that axis. This screw move is characterized by the velocity vector for the translation and the angular velocity
In physics, angular velocity (symbol or \vec, the lowercase Greek letter omega), also known as the angular frequency vector,(UP1) is a pseudovector representation of how the angular position or orientation of an object changes with time, i ...
vector in the same or opposite direction. If these two vectors are constant and along one of the principal axes of the body, no external forces are needed for this motion (moving and spinning). As an example, if gravity and drag are ignored, this is the motion of a bullet
A bullet is a kinetic projectile, a component of firearm ammunition that is shot from a gun barrel. They are made of a variety of materials, such as copper, lead, steel, polymer, rubber and even wax; and are made in various shapes and constru ...
fired from a rifled gun
A gun is a device that Propulsion, propels a projectile using pressure or explosive force. The projectiles are typically solid, but can also be pressurized liquid (e.g. in water guns or water cannon, cannons), or gas (e.g. light-gas gun). So ...
.
Biomechanics
This parameter is often used inbiomechanics
Biomechanics is the study of the structure, function and motion of the mechanical aspects of biological systems, at any level from whole organisms to Organ (anatomy), organs, Cell (biology), cells and cell organelles, using the methods of mechani ...
, when describing the motion of joint
A joint or articulation (or articular surface) is the connection made between bones, ossicles, or other hard structures in the body which link an animal's skeletal system into a functional whole.Saladin, Ken. Anatomy & Physiology. 7th ed. McGraw- ...
s of the body. For any period of time, joint motion can be seen as the movement of a single point on one articulating surface with respect to the adjacent surface (usually distal with respect to proximal). The total translation and rotations along the path of motion can be defined as the time integrals of the instantaneous translation and rotation velocities at the IHA for a given reference time.
In any single plane, the path formed by the locations of the moving instantaneous axis of rotation (IAR) is known as the 'centroid', and is used in the description of joint motion.
See also
* Corkscrew (roller coaster element) * Euler's rotation theorem – rotations without translation * Glide reflection * Helical symmetry * Line group * Screw theory *Space group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that ...
References
{{Reflist Crystallography Euclidean geometry Kinematics Machines Rigid bodies Symmetry