|
Reification (information Retrieval)
In information retrieval and natural language processing reification is the process by which an abstract idea about a person, place or thing, is turned into an explicit data model or other object created in a programming language, such as a feature set of demographichttp://cs.iit.edu/~culotta/pubs/culotta15predicting.pdf or psychographic attributes or both. By means of reification, something that was previously implicit, unexpressed, and possibly inexpressible is explicitly formulated and made available to conceptual (logical or computational) manipulation. The process by which a natural language statement is transformed so actions and events in it become Quantification (logic), quantifiable variables is semantic parsing.https://cs.stanford.edu/~pliang/papers/executable-cacm2016.pdf For example "John chased the duck furiously" can be transformed into something like :(Exists e)(chasing(e) & past_tense(e) & actor(e,John) & furiously(e) & patient(e,duck)). Another example would be " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
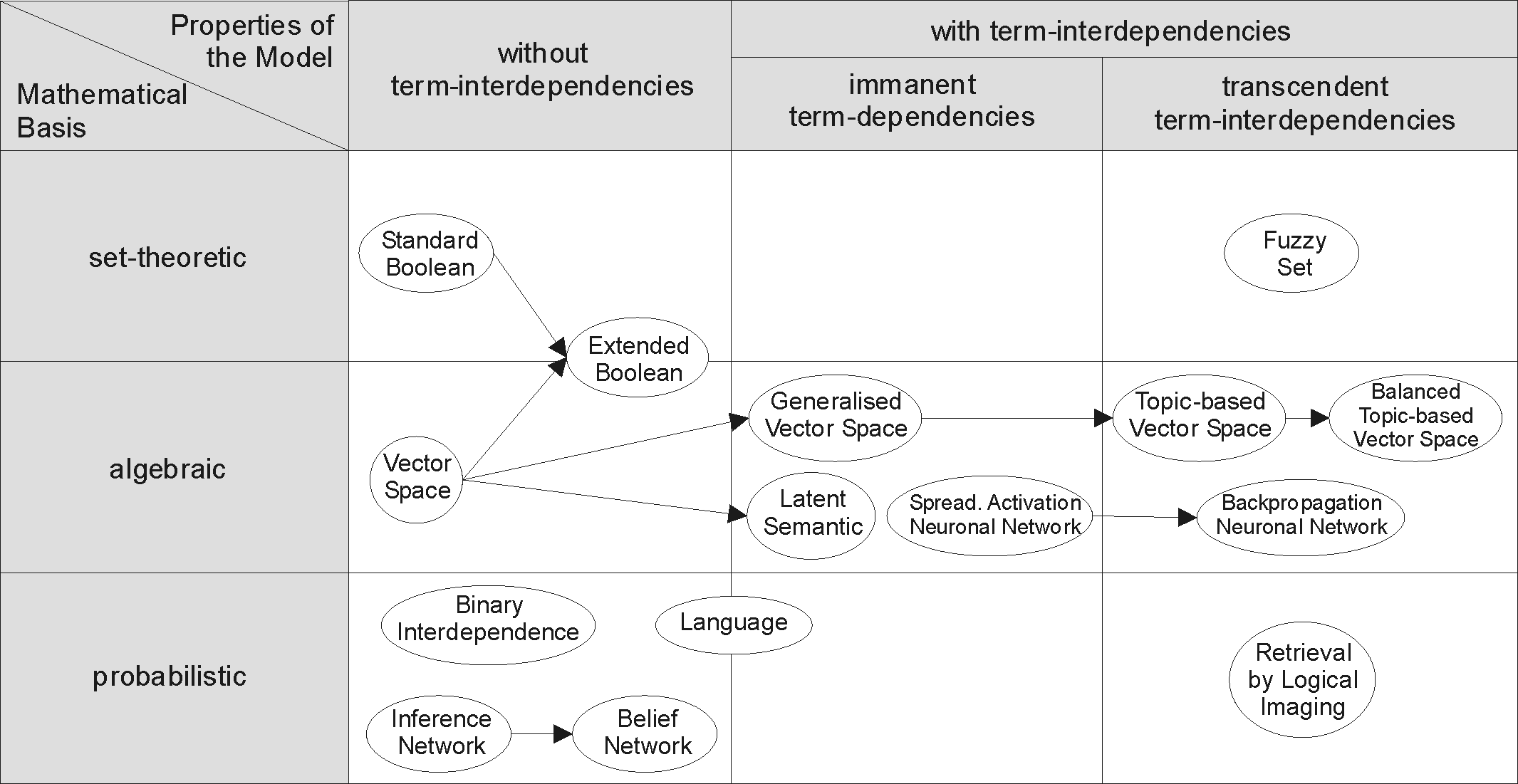
Information Retrieval
Information retrieval (IR) in computing and information science is the task of identifying and retrieving information system resources that are relevant to an Information needs, information need. The information need can be specified in the form of a search query. In the case of document retrieval, queries can be based on full-text search, full-text or other content-based indexing. Information retrieval is the science of searching for information in a document, searching for documents themselves, and also searching for the metadata that describes data, and for databases of texts, images or sounds. Automated information retrieval systems are used to reduce what has been called information overload. An IR system is a software system that provides access to books, journals and other documents; it also stores and manages those documents. Web search engines are the most visible IR applications. Overview An information retrieval process begins when a user enters a query into the sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Language Processing
Natural language processing (NLP) is a subfield of computer science and especially artificial intelligence. It is primarily concerned with providing computers with the ability to process data encoded in natural language and is thus closely related to information retrieval, knowledge representation and computational linguistics, a subfield of linguistics. Major tasks in natural language processing are speech recognition, text classification, natural-language understanding, natural language understanding, and natural language generation. History Natural language processing has its roots in the 1950s. Already in 1950, Alan Turing published an article titled "Computing Machinery and Intelligence" which proposed what is now called the Turing test as a criterion of intelligence, though at the time that was not articulated as a problem separate from artificial intelligence. The proposed test includes a task that involves the automated interpretation and generation of natural language ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantification (logic)
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first-order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The most commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic: each can be defined in terms of the other using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantic Parsing
Semantic parsing is the task of converting a natural language utterance to a logical form: a machine-understandable representation of its meaning. Semantic parsing can thus be understood as extracting the precise meaning of an utterance. Applications of semantic parsing include machine translation, question answering,Berant, Jonathan, et al"Semantic Parsing on Freebase from Question-Answer Pairs."EMNLP. Vol. 2. No. 5. 2013. ontology induction, automated reasoning, and code generation. The phrase was first used in the 1970s by Yorick Wilks as the basis for machine translation programs working with only semantic representations. Semantic parsing is one of the important tasks in computational linguistics and natural language processing. Semantic parsing maps text to formal meaning representations. This contrasts with semantic role labeling and other forms of shallow semantic processing, which do not aim to produce complete formal meanings. In computer vision, semantic parsing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First-order Logic
First-order logic, also called predicate logic, predicate calculus, or quantificational logic, is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables. Rather than propositions such as "all humans are mortal", in first-order logic one can have expressions in the form "for all ''x'', if ''x'' is a human, then ''x'' is mortal", where "for all ''x"'' is a quantifier, ''x'' is a variable, and "... ''is a human''" and "... ''is mortal''" are predicates. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic, such as set theory, a theory for groups,A. Tarski, ''Undecidable Theories'' (1953), p. 77. Studies in Logic and the Foundation of Mathematics, North-Holland or a formal theory o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automated Theorem Prover
Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major motivating factor for the development of computer science. Logical foundations While the roots of formalized logic go back to Aristotle, the end of the 19th and early 20th centuries saw the development of modern logic and formalized mathematics. Frege's ''Begriffsschrift'' (1879) introduced both a complete propositional calculus and what is essentially modern predicate logic. His '' Foundations of Arithmetic'', published in 1884, expressed (parts of) mathematics in formal logic. This approach was continued by Russell and Whitehead in their influential ''Principia Mathematica'', first published 1910–1913, and with a revised second edition in 1927. Russell and Whitehead thought they could derive all mathematical truth using axioms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Checker
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software systems, where the specification contains liveness requirements (such as avoidance of livelock) as well as safety requirements (such as avoidance of states representing a system crash). In order to solve such a problem algorithmically, both the model of the system and its specification are formulated in some precise mathematical language. To this end, the problem is formulated as a task in logic, namely to check whether a structure satisfies a given logical formula. This general concept applies to many kinds of logic and many kinds of structures. A simple model-checking problem consists of verifying whether a formula in the propositional logic is satisfied by a given structure. Overview Property checking is used for verification when two de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skolem Constant
In mathematical logic, a formula of first-order logic is in Skolem normal form if it is in prenex normal form with only universal first-order quantifiers. Every first-order formula may be converted into Skolem normal form while not changing its satisfiability via a process called Skolemization (sometimes spelled Skolemnization). The resulting formula is not necessarily equivalent to the original one, but is equisatisfiable with it: it is satisfiable if and only if the original one is satisfiable. Reduction to Skolem normal form is a method for removing existential quantifiers from formal logic statements, often performed as the first step in an automated theorem prover. Examples The simplest form of Skolemization is for existentially quantified variables that are not inside the scope of a universal quantifier. These may be replaced simply by creating new constants. For example, \exists x P(x) may be changed to P(c), where c is a new constant (does not occur anywhere el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donkey Sentence
In semantics, a donkey sentence is a sentence containing a pronoun which is semantically bound but syntactically free. They are a classic puzzle in formal semantics and philosophy of language because they are fully grammatical and yet defy straightforward attempts to generate their formal language equivalents. In order to explain how speakers are able to understand them, semanticists have proposed a variety of formalisms including systems of dynamic semantics such as Discourse representation theory. Their name comes from the example sentence "Every farmer who owns a donkey beats it", in which "it" acts as a donkey pronoun because it is semantically but not syntactically bound by the indefinite noun phrase "a donkey". The phenomenon is known as donkey anaphora. Examples The following sentences are examples of donkey sentences. * ("Every man who owns a donkey sees it") — Walter Burley (1328), *Every farmer who owns a donkey beats it. *If a farmer owns a donkey, he beats it. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drinker Paradox
The drinker paradox (also known as the drinker's theorem, the drinker's principle, or the drinking principle) is a theorem of classical predicate logic that can be stated as "There is someone in the pub such that, if he or she is drinking, then everyone in the pub is drinking." It was popularised by the mathematical logician Raymond Smullyan, who called it the "drinking principle" in his 1978 book ''What Is the Name of this Book?'' The apparently paradoxical nature of the statement comes from the way it is usually stated in natural language. It seems counterintuitive both that there could be a person who is ''causing'' the others to drink, or that there could be a person such that all through the night that one person were always the ''last'' to drink. The first objection comes from confusing formal "if then" statements with causation (see Correlation does not imply causation or Relevance logic for logics that demand relevant relationships between premise and consequent, unlike ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonfirstorderizability
In formal logic, nonfirstorderizability is the inability of a natural-language statement to be adequately captured by a formula of first-order logic. Specifically, a statement is nonfirstorderizable if there is no formula of first-order logic which is true in a model if and only if the statement holds in that model. Nonfirstorderizable statements are sometimes presented as evidence that first-order logic is not adequate to capture the nuances of meaning in natural language. The term was coined by George Boolos in his paper "To Be is to Be a Value of a Variable (or to Be Some Values of Some Variables)". Reprinted in Quine argued that such sentences call for second-order symbolization, which can be interpreted as plural quantification over the same domain as first-order quantifiers use, without postulation of distinct "second-order objects" (properties, sets, etc.). Examples Geach-Kaplan sentence A standard example is the '' Geach– Kaplan sentence'': "Some critics admire on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reification (computer Science)
In computer science, reification is the process by which an abstract idea about a computer program, program is turned into an explicit data model or other object created in a programming language. A computable/addressable object—a ''resource''—is created in a system as a proxy for a non computable/addressable object. By means of reification, something that was previously implicit, unexpressed, and possibly inexpressible is explicitly formulated and made available to conceptual (logical or computational) manipulation. Informally, reification is often referred to as "making something a first-class citizen" within the scope of a particular system. Some aspect of a system can be reified at ''language design time'', which is related to Reflection (computer science), reflection in programming languages. It can be applied as a stepwise refinement at ''system design time''. Reification is one of the most frequently used techniques of conceptual analysis and knowledge representation. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |