|
Quadratic Average
In mathematics, the root mean square (abbrev. RMS, or rms) of a set of values is the square root of the set's mean square. Given a set x_i, its RMS is denoted as either x_\mathrm or \mathrm_x. The RMS is also known as the quadratic mean (denoted M_2), a special case of the generalized mean. The RMS of a continuous function is denoted f_\mathrm and can be defined in terms of an integral of the square of the function. In estimation theory, the root-mean-square deviation of an estimator measures how far the estimator strays from the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In the case of a set of ''n'' values \, the RMS is : x_\text = \sqrt. The corresponding formula for a continuous function (or waveform) ''f''(''t'') defined over the interval T_1 \le t \le T_2 is : f_\text = \sqrt , and the RMS for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave Voltages
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the position an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than , called ''floor'' of or \lfloor x\rfloor. Then, the fractional part can be formulated as a difference: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. The fractional part of logarithms, specifically, is also known as the mantissa; by contrast with the mantissa, the integral part of a logarithm is called its ''characteristic''. The word ''mantissa'' was introduced by Henry Briggs. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point, such as the decimal point in English. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duty Cycle
A duty cycle or power cycle is the fraction of one period in which a signal or system is active. Duty cycle is commonly expressed as a percentage or a ratio. A period is the time it takes for a signal to complete an on-and-off cycle. As a formula, a duty cycle (%) may be expressed as: :D = \frac \times 100\% Equally, a duty cycle (ratio) may be expressed as: :D = \frac where D is the duty cycle, PW is the pulse width (pulse active time), and T is the total period of the signal. Thus, a 60% duty cycle means the signal is on 60% of the time and off 40% of the time. The "on time" for a 60% duty cycle could be a fraction of a second, a day, or even a week, depending on the length of the period. Duty cycles can be used to describe the percent time of an active signal in an electrical device such as the power switch in a switching power supply or the firing of action potentials by a living system such as a neuron. Some publications use \alpha as the symbol for duty cycle. As a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-phase Electric Power
Three-phase electric power (abbreviated 3ϕ) is a common type of alternating current (AC) used in electricity generation, transmission, and distribution. It is a type of polyphase system employing three wires (or four including an optional neutral return wire) and is the most common method used by electrical grids worldwide to transfer power. Three-phase electrical power was developed in the 1880s by several people. In three-phase power, the voltage on each wire is 120 degrees phase shifted relative to each of the other wires. Because it is an AC system, it allows the voltages to be easily stepped up using transformers to high voltage for transmission and back down for distribution, giving high efficiency. A three-wire three-phase circuit is usually more economical than an equivalent two-wire single-phase circuit at the same line-to-ground voltage because it uses less conductor material to transmit a given amount of electrical power. Three-phase power is mainly used dire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pulse Wave
A pulse wave or pulse train or rectangular wave is a non-sinusoidal waveform that is the periodic version of the rectangular function. It is held high a percent each cycle ( period) called the duty cycle and for the remainder of each cycle is low. A duty cycle of 50% produces a square wave, a specific case of a rectangular wave. The average level of a rectangular wave is also given by the duty cycle. A pulse wave is used as a basis for other waveforms that modulate an aspect of the pulse wave. In pulse-width modulation (PWM) information is encoded by varying the duty cycle of a pulse wave. Pulse-amplitude modulation (PAM) encodes information by varying the amplitude. Frequency-domain representation The Fourier series expansion for a rectangular pulse wave with period T, amplitude A and pulse length \tau is x(t) = A \frac + \frac \sum_^ \left(\frac \sin\left(\pi n\frac\right) \cos\left(2\pi nft\right)\right) where f = \frac. Equivalently, if duty cycle d = \frac is used, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
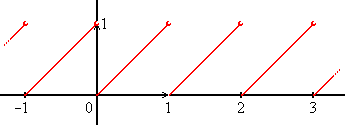
Sawtooth Wave
The sawtooth wave (or saw wave) is a kind of non-sinusoidal waveform. It is so named based on its resemblance to the teeth of a plain-toothed saw with a zero rake angle. A single sawtooth, or an intermittently triggered sawtooth, is called a ramp waveform. The convention is that a sawtooth wave ramps upward and then sharply drops. In a reverse (or inverse) sawtooth wave, the wave ramps downward and then sharply rises. It can also be considered the extreme case of an asymmetric triangle wave. The equivalent piecewise linear functions x(t) = t - \lfloor t \rfloor x(t) = t \bmod 1 based on the floor function of time ''t'' is an example of a sawtooth wave with period 1. A more general form, in the range −1 to 1, and with period ''p'', is 2\left( - \left\lfloor + \right\rfloor\right) This sawtooth function has the same phase as the sine function. While a square wave is constructed from only odd harmonics, a sawtooth wave's sound is harsh and clear and its spectrum cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Wave
A triangular wave or triangle wave is a non-sinusoidal waveform named for its triangular shape. It is a periodic, piecewise linear, continuous real function. Like a square wave, the triangle wave contains only odd harmonics. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse). Definitions Definition A triangle wave of period ''p'' that spans the range , 1is defined as x(t) = 2 \left, \frac - \left\lfloor \frac + \frac \right\rfloor \, where \lfloor\ \rfloor is the floor function. This can be seen to be the absolute value of a shifted sawtooth wave. For a triangle wave spanning the range the expression becomes x(t)= 2 \left , 2 \left( \frac - \left\lfloor \frac + \frac \right\rfloor \right) \ - 1. A more general equation for a triangle wave with amplitude a and period p using the modulo operation and absolute value is y(x) = \frac \left, \left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverter (electrical)
A power inverter, inverter, or invertor is a power electronic device or circuitry that changes direct current (DC) to alternating current (AC). The resulting AC frequency obtained depends on the particular device employed. Inverters do the opposite of rectifiers which were originally large electromechanical devices converting AC to DC. The input voltage, output voltage and frequency, and overall power handling depend on the design of the specific device or circuitry. The inverter does not produce any power; the power is provided by the DC source. A power inverter can be entirely electronic or maybe a combination of mechanical effects (such as a rotary apparatus) and electronic circuitry. Static inverters do not use moving parts in the conversion process. Power inverters are primarily used in electrical power applications where high currents and voltages are present; circuits that perform the same function for electronic signals, which usually have very low currents and vol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Wave (waveform)
A square wave is a non-sinusoidal waveform, non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions between minimum and maximum are instantaneous. The square wave is a special case of a pulse wave which allows arbitrary durations at minimum and maximum amplitudes. The ratio of the high period to the total period of a pulse wave is called the duty cycle. A true square wave has a 50% duty cycle (equal high and low periods). Square waves are often encountered in electronics and signal processing, particularly digital electronics and digital signal processing. Its stochastic counterpart is a two-state trajectory. Origin and uses Square waves are universally encountered in digital switching circuits and are naturally generated by binary (two-level) logic devices. They are used as timing references or "clock signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase (waves), phase) are linear combination, linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Current
Direct current (DC) is one-directional electric current, flow of electric charge. An electrochemical cell is a prime example of DC power. Direct current may flow through a conductor (material), conductor such as a wire, but can also flow through semiconductors, electrical insulation, insulators, or even through a vacuum as in electron beam, electron or ion beams. The electric current flows in a constant direction, distinguishing it from alternating current (AC). A archaism, term formerly used for this type of current was galvanic current. The abbreviations ''AC'' and ''DC'' are often used to mean simply ''alternating'' and ''direct'', as when they modify ''Electric current, current'' or ''voltage''. Direct current may be converted from an alternating current supply by use of a rectifier, which contains Electronics, electronic elements (usually) or electromechanical elements (historically) that allow current to flow only in one direction. Direct current may be converted into alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |