|
Pearson Symbol
The Pearson symbol, or Pearson notation, is used in crystallography as a means of describing a crystal structure. It was originated by William Burton Pearson and is used extensively in Pearson's handbook of crystallographic data for intermetallic phases. The symbol is made up of two letters followed by a number. For example: * Diamond structure, cF8 * Rutile structure, tP6 Construction The two letters in the Pearson symbol specify the Bravais lattice, and more specifically, the lower-case letter specifies the Crystal system, crystal family, while the upper-case letter the Lattice (group), lattice type. The number at the end of the Pearson symbol gives the number of the atoms in the conventional unit cell (atoms which satisfy 1 > x,y,z \geq 0 for the atom's position (x,y,z) in the unit cell). [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In July 2012, the United Nations recognised the importance of the science of crystallography by proclaiming 2014 the International Year of Crystallography.UN announcement "International Year of Crystallography" iycr2014.org. 12 July 2012 Crystallography is a broad topic, and many of its subareas, such as X-ray crystallography, are themselves important scientific topics. Crystallography ranges from the fundamentals of crystal structure to the mathematics of Crystal system, crystal geometry, including those that are Aperiodic crystal, not periodic or quasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Structure
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter. The smallest group of particles in a material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice. The lengths of principal axes/edges, of the unit cell and angles between them are lattice constants, also called ''lattice parameters'' or ''cell parameters''. The symmetry properties of a crystal are described by the concept of space groups. All possible symmetric arrangements of particles in three-dimensional space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Burton Pearson
William is a masculine given name of Germanic origin. It became popular in England after the Norman conquest in 1066,All Things William"Meaning & Origin of the Name"/ref> and remained so throughout the Middle Ages and into the modern era. It is sometimes abbreviated "Wm." Shortened familiar versions in English include Will or Wil, Wills, Willy, Willie, Bill, Billie, and Billy. A common Irish form is Liam. Scottish diminutives include Wull, Willie or Wullie (as in Oor Wullie). Female forms include Willa, Willemina, Wilma and Wilhelmina. Etymology William is related to the German given name ''Wilhelm''. Both ultimately descend from Proto-Germanic ''*Wiljahelmaz'', with a direct cognate also in the Old Norse name ''Vilhjalmr'' and a West Germanic borrowing into Medieval Latin ''Willelmus''. The Proto-Germanic name is a compound of *''wiljô'' "will, wish, desire" and *''helmaz'' "helm, helmet".Hanks, Hardcastle and Hodges, ''Oxford Dictionary of First Names'', Oxford Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of electricity, and insoluble in water. Another solid form of carbon known as graphite is the Chemical stability, chemically stable form of carbon at Standard temperature and pressure, room temperature and pressure, but diamond is metastable and converts to it at a negligible rate under those conditions. Diamond has the highest Scratch hardness, hardness and thermal conductivity of any natural material, properties that are used in major industrial applications such as cutting and polishing tools. Because the arrangement of atoms in diamond is extremely rigid, few types of impurity can contaminate it (two exceptions are boron and nitrogen). Small numbers of lattice defect, defects or impurities (about one per million of lattice atoms) can color ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rutile
Rutile is an oxide mineral composed of titanium dioxide (TiO2), the most common natural form of TiO2. Rarer polymorphs of TiO2 are known, including anatase, akaogiite, and brookite. Rutile has one of the highest refractive indices at visible wavelengths of any known crystal and also exhibits a particularly large birefringence and high dispersion. Owing to these properties, it is useful for the manufacture of certain optical elements, especially polarization optics, for longer visible and infrared wavelengths up to about 4.5 micrometres. Natural rutile may contain up to 10% iron and significant amounts of niobium and tantalum. Rutile derives its name from the Latin ('red'), in reference to the deep red color observed in some specimens when viewed by transmitted light. Rutile was first described in 1803 by Abraham Gottlob Werner using specimens obtained in Horcajuelo de la Sierra, Madrid (Spain), which is consequently the type locality. Occurrence Rutile is a comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bravais Lattice
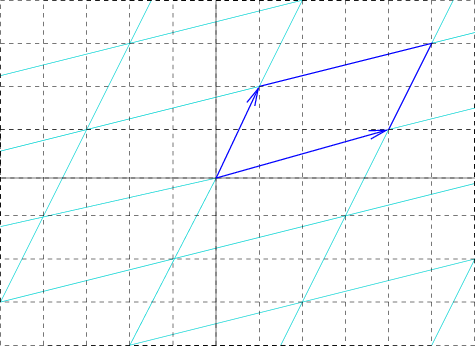
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by : \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n_3 \mathbf_3, where the ''ni'' are any integers, and a''i'' are ''primitive translation vectors'', or ''primitive vectors'', which lie in different directions (not necessarily mutually perpendicular) and span the lattice. The choice of primitive vectors for a given Bravais lattice is not unique. A fundamental aspect of any Bravais lattice is that, for any choice of direction, the lattice appears exactly the same from each of the discrete lattice points when looking in that chosen direction. The Bravais lattice concept is used to formally define a ''crystalline arrangement'' and its (finite) frontiers. A crystal is made up of one or more atoms, called the ''basis'' or ''motif'', at each lattice point. The ''basis'' may consist of atoms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal System
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices (an infinite array of discrete points). Space groups (symmetry groups of a configuration in space) are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family. The seven crystal systems are ''triclinic'', ''monoclinic'', ''orthorhombic'', ''tetragonal'', ''trigonal'', ''hexagonal'', and ''cubic''. Informally, two crystals are in the same crystal system if they have similar symmetries (though there are many exceptions). Classifications Crystals can be classified in three ways: lattice systems, crystal systems and crystal families. The various classifications are often confused: in particular the trigonal crystal system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group)
In geometry and group theory, a lattice in the real coordinate space \mathbb^n is an infinite set of points in this space with the properties that coordinate-wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension n which spans the vector space \mathbb^n. For any basis of \mathbb^n, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ..., for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IUPAC Nomenclature Of Inorganic Chemistry 2005
Nomenclature of Inorganic Chemistry, IUPAC Recommendations 2005 is the 2005 version of ''Nomenclature of Inorganic Chemistry'' (which is informally called the Red Book). It is a collection of rules for naming inorganic compounds, as recommended by the International Union of Pure and Applied Chemistry (IUPAC). Summary The 2005 edition replaces their previous recommendations ''Nomenclature The Red Book of Inorganic Chemistry, IUPAC Recommendations 1990 (Red Book I)'', and "where appropriate" (sic) ''Nomenclature of Inorganic Chemistry II, IUPAC Recommendations 2000 (Red Book II)''. The recommendations take up over 300 pages''Nomenclature of Inorganic Chemistry IUPAC Recommendations'' 2005 ed. N. G. Connelly et al. RSC Publishing https://iupac.org/what-we-do/books/redbook/ and the full text can be downloaded from IUPAC. Corrections have been issued. Apart from a reorganisation of the content, there is a new section on organometallics and a formal element list to be used in place o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inorganic Crystal Structure Database
Inorganic Crystal Structure Database (ICSD) is a chemical database founded in 1978 by Günter Bergerhoff at the University of Bonn in Germany and I. D. Brown at McMaster University in Canada. It is now produced by FIZ Karlsruhe in Europe and the U.S. National Institute of Standards and Technology. It seeks to contain information on all inorganic crystal structures published since 1913, including pure elements, minerals, metals, and intermetallic compounds (with atomic coordinates). ICSD contains over 210,000 entries and is updated twice a year. A Windows Windows is a Product lining, product line of Proprietary software, proprietary graphical user interface, graphical operating systems developed and marketed by Microsoft. It is grouped into families and subfamilies that cater to particular sec ...-based PC version has been developed in co-operation with the National Institute of Standards and Technology (NIST), and a PHP-MySQL web based version in co-operation with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |