|
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval. A limaçon is a bicircular rational plane algebraic curve of degree 4. History The earliest formal research on limaçons is generally attributed to Étienne Pascal, f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
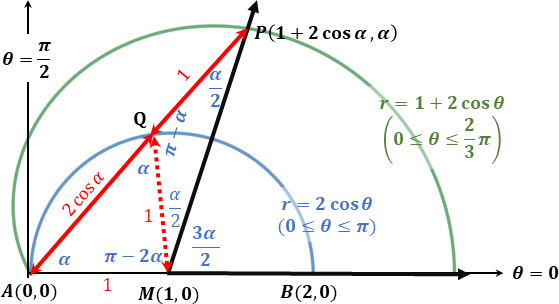
Limaçon Trisectrix
In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin. Specification and loop structure The limaçon trisectrix specified as a polar equation is :r= a(1+2\cos\theta). The constant a may be positive or negative. The two curves with constants a and -a are reflections of each other across the line \theta=\pi/2. The period of r= a(1+2\cos\theta) is 2\pi given the period of the sinusoid \cos\theta. The limaçon trisectrix is composed of two loops. * The outer loop is defined when 1+2\cos\theta\ge0 on the polar angle interval -2\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trisectrix
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle with ruler and compass and this curve as an additional tool. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of construction. There is a variety of such curves and the methods used to construct an angle trisector differ according to the curve. Examples include: * Limaçon trisectrix (some sources refer to this curve as simply the trisectrix.) * Trisectrix of Maclaurin * Equilateral trefoil (a.k.a. Longchamps' Trisectrix) * Tschirnhausen cubic (a.k.a. Catalan's trisectrix and L'Hôpital's cubic) * Durer's folium * Cubic parabola * Hyperbola with eccentricity 2 * Rose curve specified by a sinusoid with angular frequency of one-third. * Parabola A related concept is a sectrix, which is a curve which can be used to divide an arbitra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid specified by either the cosine or sine functions with no phase angle that is plotted in polar coordinates. Rose curves or "rhodonea" were named by the Italian mathematician who studied them, Guido Grandi, between the years 1723 and 1728. General overview Specification A rose is the set of points in polar coordinates specified by the polar equation :r=a\cos(k\theta) or in Cartesian coordinates using the parametric equations :x=r\cos(\theta)=a\cos(k\theta)\cos(\theta) :y=r\sin(\theta)=a\cos(k\theta)\sin(\theta). Roses can also be specified using the sine function. Since :\sin(k \theta) = \cos\left( k \theta - \frac \right) = \cos\left( k \left( \theta-\frac \right) \right). Thus, the rose specified by \,r=a\sin(k\theta) is identical to that specified by \,r = a\cos(k\theta) rotated counter-clockwise by \pi/2k radians, which is one-quarter the period of either sinusoid. Since they are specified using the cosine or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history The history of Europe is traditionally divided into four time periods: prehistoric Europe (prior to about 800 BC), classical antiquity (800 BC to AD 500), the Middle Ages (AD 500 to AD 1500), and the modern era (since AD 1500). The first early ... marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas and achievements of classical antiquity. It occurred after the Crisis of the Late Middle Ages and was associated with great social change. In addition to the standard periodization, proponents of a "long Renaissance" may put its beginning in the 14th century and its end in the 17th century. The traditional view focuses more on the Early modern period, early modern aspects of the Renaissance and argues that it was a break from the past, but many historians today focus more on its medieval a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surfa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflection Point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa. For the graph of a function of differentiability class (''f'', its first derivative ''f, and its second derivative ''f'''', exist and are continuous), the condition ''f'' = 0'' can also be used to find an inflection point since a point of ''f'' = 0'' must be passed to change ''f'''' from a positive value (concave upward) to a negative value (concave downward) or vice versa as ''f'''' is continuous; an inflection point of the curve is where ''f'' = 0'' and changes its sign at the point (from positive to negative or from negative to positive). A point where the second derivative vanishes bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acnode
An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are " isolated point or hermit point". For example the equation :f(x,y)=y^2+x^2-x^3=0 has an acnode at the origin, because it is equivalent to :y^2 = x^2 (x-1) and x^2(x-1) is non-negative only when x ≥ 1 or x = 0. Thus, over the ''real'' numbers the equation has no solutions for x < 1 except for (0, 0). In contrast, over the complex numbers the origin is not isolated since square roots of negative real numbers exist. In fact, the complex solution set of a polynomial equation in two complex variables can never have an isolated point. An acnode is a critical point, or singularity, of the defining polynomial function, in the sense that both partial derivatives and vanish. Further ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal Spiral
In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates :r^n = a^n \cos(n \theta)\, where is a nonzero constant and is a rational number other than 0. With a rotation about the origin, this can also be written :r^n = a^n \sin(n \theta).\, The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including: * Rectangular hyperbola () * Line () * Parabola () * Tschirnhausen cubic () * Cayley's sextet () * Cardioid () * Circle () * Lemniscate of Bernoulli () The curves were first studied by Colin Maclaurin. Equations Differentiating :r^n = a^n \cos(n \theta)\, and eliminating ''a'' produces a differential equation for ''r'' and θ: :\frac\cos n\theta + r\sin n\theta =0. Then :\left(\frac,\ r\frac\right)\cos n\theta \frac = \left(-r\sin n\theta ,\ r \cos n\theta \right) = r\left(-\sin n\theta ,\ \cos n\theta \right) w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates—the magnitude or ''modulus'' of the product is the product of the two absolute values, or moduli, and the angle or ''argument'' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes known as the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol ''z'', which can be separated into its real (''x'') an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |