|
Join Count Statistics
Join count statistics are a method of spatial analysis used to assess the degree of association, in particular the autocorrelation, of Categorical variable, categorical variables distributed over a spatial map. They were originally introduced by Australian statistician P. A. P. Moran. Join count statistics have found widespread use in econometrics, remote sensing and ecology.Dale MR, Fortin MJ. Spatial analysis: a guide for ecologists. Cambridge University Press; 2014 Sep 11. Join count statistics can be computed in a number of software packages including PASSaGE, GeoDA, PySAL and spdep. Binary data Given binary data x_i \in \ distributed over N spatial sites, where the neighbour relations between regions i and j are encoded in the spatial weight matrix :w_ = \begin 1 \qquad &i\textj\\ 0 &\text \end the join count statistics are defined as : J = J_ + J_ + J_ Where : J_ = \frac\sum_ w_ x_i x_j : J_ = \frac\sum_ w_ (x_i-x_j)^2 : J_ = \frac\sum_ w_ (1-x_i) (1-x_j) : J = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Analysis
Spatial analysis is any of the formal Scientific technique, techniques which study entities using their topological, geometric, or geographic properties, primarily used in Urban design, Urban Design. Spatial analysis includes a variety of techniques using different analytic approaches, especially ''spatial statistics''. It may be applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, or to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is geospatial analysis, the technique applied to structures at the human scale, most notably in the analysis of geographic data. It may also applied to genomics, as in Spatial transcriptomics, transcriptomics data, but is primarily for spatial data. Complex issues arise in spatial analysis, many of which are neither clearly defined nor completely resolved, but form the basis for current resear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Process
In probability and statistics, a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables ''X''''i'' are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin (but with consistent unfairness). Every variable ''X''''i'' in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes (such as the process for a six-sided die); this generalization is known as the Bernoulli scheme. The problem of determining the process, given only a limited sample of Bernoulli trials, may be called the problem of checking whether a coin is fair. Definition A ''Bernoulli process'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indicator Function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , then the indicator function of is the function \mathbf_A defined by \mathbf_\!(x) = 1 if x \in A, and \mathbf_\!(x) = 0 otherwise. Other common notations are and \chi_A. The indicator function of is the Iverson bracket of the property of belonging to ; that is, \mathbf_(x) = \left x\in A\ \right For example, the Dirichlet function is the indicator function of the rational numbers as a subset of the real numbers. Definition Given an arbitrary set , the indicator function of a subset of is the function \mathbf_A \colon X \mapsto \ defined by \operatorname\mathbf_A\!( x ) = \begin 1 & \text x \in A \\ 0 & \text x \notin A \,. \end The Iverson bracket provides the equivalent notation \left x\in A\ \right/math> or that can be used instead of \mathbf_\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Join Counts For 3 Classes
Join may refer to: * Join (law), to include additional counts or additional defendants on an indictment *In mathematics: ** Join (mathematics), a least upper bound of sets orders in lattice theory ** Join (topology), an operation combining two topological spaces ** Join (category theory), an operation combining two categories ** Join (simplicial sets), an operation combining two simplicial sets ** Join (sigma algebra), a refinement of sigma algebras ** Join (algebraic geometry), a union of lines between two varieties *In computing: ** Join (relational algebra), a binary operation on tuples corresponding to the relation join of SQL *** Join (SQL), relational join, a binary operation on SQL and relational database tables *** join (Unix), a Unix command similar to relational join ** Join-calculus, a process calculus developed at INRIA for the design of distributed programming languages *** Join-pattern, generalization of Join-calculus *** Joins (concurrency library), a concurrent compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiple Comparisons Problem
Multiple comparisons, multiplicity or multiple testing problem occurs in statistics when one considers a set of statistical inferences simultaneously or estimates a subset of parameters selected based on the observed values. The larger the number of inferences made, the more likely erroneous inferences become. Several statistical techniques have been developed to address this problem, for example, by requiring a stricter significance threshold for individual comparisons, so as to compensate for the number of inferences being made. Methods for family-wise error rate give the probability of false positives resulting from the multiple comparisons problem. History The problem of multiple comparisons received increased attention in the 1950s with the work of statisticians such as Tukey and Scheffé. Over the ensuing decades, many procedures were developed to address the problem. In 1996, the first international conference on multiple comparison procedures took place in Tel Aviv. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
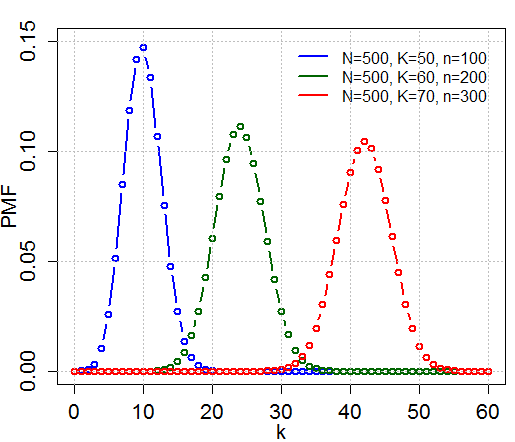
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a Probability distribution#Discrete probability distribution, discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite Statistical population, population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of Binary variable, two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Getis–Ord Statistics
Getis–Ord statistics, also known as Gi*, are used in spatial analysis to measure the local and global spatial autocorrelation. Developed by statisticians Arthur Getis and J. Keith Ord they are commonly used for ''Hot Spot Analysis'' to identify where features with high or low values are spatially clustered in a statistically significant way. Getis-Ord statistics are available in a number of software libraries such as CrimeStat, GeoDa, ArcGIS, PySAL and R (programming language), R. Local statistics There are two different versions of the statistic, depending on whether the data point at the target location i is included or not : G_i = \frac : G_i^* = \frac Here x_i is the value observed at the i^ spatial site and w_ is the spatial weight matrix which constrains which sites are connected to one another. For G_i^* the denominator is constant across all observations. A value larger (or smaller) than the mean suggests a hot (or cold) spot corresponding to a high-high (or low-l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luc Anselin
Luc E. Anselin (born December 1, 1953) is one of the developers of the field of spatial econometrics and the Stein-Freiler Distinguished Service Professor of Sociology and the College at the University of Chicago. Life and contributions Luc Anselin was previously the Regents' Professor, Walter Isard Chair and Director of the School of Geographical Sciences and Urban Planning at Arizona State University (ASU) where he attracted some of the leading spatial econometrics scholars. He also founded and directed the GeoDa Center for Geospatial Analysis and Computation at ASU to develop, implement, apply, and disseminate spatial analysis methods. In 2016, the GeoDa Center for Geospatial Analysis relocated to the University of Chicago.spatial.uchicago.edu. He held prior appointments at the University of Illinois, Urbana-Champaign, University of Texas at Dallas, West Virginia University, the University of California, Santa Barbara and the Ohio State University. His joint appointments include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation Test
A permutation test (also called re-randomization test or shuffle test) is an exact statistical hypothesis test. A permutation test involves two or more samples. The (possibly counterfactual) null hypothesis is that all samples come from the same distribution H_0: F=G. Under the null hypothesis, the distribution of the test statistic is obtained by calculating all possible values of the test statistic under possible rearrangements of the observed data. Permutation tests are, therefore, a form of resampling. Permutation tests can be understood as surrogate data testing where the surrogate data under the null hypothesis are obtained through permutations of the original data. In other words, the method by which treatments are allocated to subjects in an experimental design is mirrored in the analysis of that design. If the labels are exchangeable under the null hypothesis, then the resulting tests yield exact significance levels; see also exchangeability. Confidence intervals can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
The null hypothesis (often denoted ''H''0) is the claim in scientific research that the effect being studied does not exist. The null hypothesis can also be described as the hypothesis in which no relationship exists between two sets of data or variables being analyzed. If the null hypothesis is true, any experimentally observed effect is due to chance alone, hence the term "null". In contrast with the null hypothesis, an alternative hypothesis (often denoted ''H''A or ''H''1) is developed, which claims that a relationship does exist between two variables. Basic definitions The null hypothesis and the ''alternative hypothesis'' are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength of the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at different points in time. The analysis of autocorrelation is a mathematical tool for identifying repeating patterns or hidden periodicities within a signal obscured by noise. Autocorrelation is widely used in signal processing, time domain and time series analysis to understand the behavior of data over time. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Various time series models incorporate autocorrelation, such as unit root processes, trend-stationary processes, autoregressive processes, and moving average processes. Autocorrelation of stochastic processes In statistics, the autocorrelation of a real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the p-value, ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is said to be ''statistically significant'', by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or Observational study, observation that involves drawing a Sampling (statistics), sample from a Statistical population, population, there is always the possibility that an observed effect would have occurred due to sampling error al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |