|
Hamming Code
In computer science and telecommunications, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data. In mathematical terms, Hamming codes are a class of binary linear code. For each integer there is a code-word with block length and message length . Hence the rate of Hamming codes is , which is the highest p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
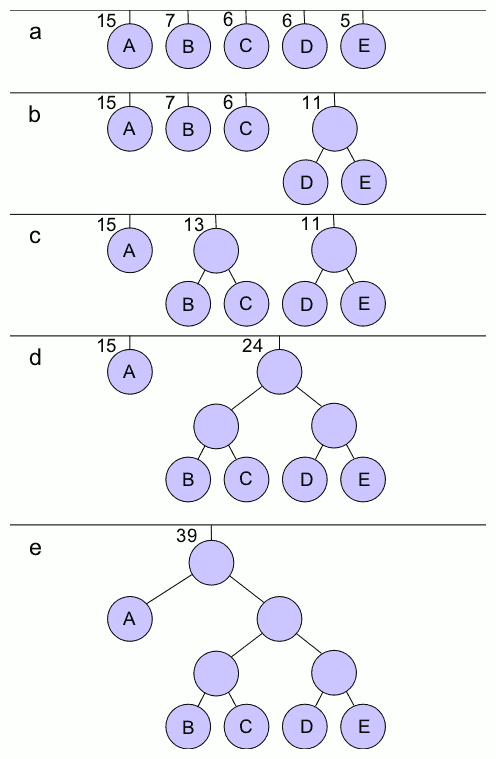
Huffman Coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Doctor of Science, Sc.D. student at Massachusetts Institute of Technology, MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear time, linear to the number of input weigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ECC Memory
Error correction code memory (ECC memory) is a type of computer data storage that uses an error correction code (ECC) to detect and correct ''n''-bit data corruption which occurs in memory. Typically, ECC memory maintains a memory system immune to single-bit errors: the data that is read from each word is always the same as the data that had been written to it, even if one of the bits actually stored has been flipped to the wrong state. Most non-ECC memory cannot detect errors, although some non-ECC memory with parity support allows detection but not correction. ECC memory is used in most computers where data corruption cannot be tolerated, like industrial control applications, critical databases, and infrastructural memory caches. Concept Error correction codes protect against undetected data corruption and are used in computers where such corruption is unacceptable, examples being scientific and financial computing applications, or in database and file servers. ECC can a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Syndrome
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel. Notation C \subset \mathbb_2^n is considered a binary code with the length n; x,y shall be elements of \mathbb_2^n; and d(x,y) is the distance between those elements. Ideal observer decoding One may be given the message x \in \mathbb_2^n, then ideal observer decoding generates the codeword y \in C. The process results in this solution: :\mathbb(y \mbox \mid x \mbox) For example, a person can choose the codeword y that is most likely to be received as the message x after transmission. Decoding conventions Each codeword does not have an expected possibility: there may be more than one codeword with an equal likelihood of mutating into the received message. In such a case, the sender and receiver(s) mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamming Distance
In information theory, the Hamming distance between two String (computer science), strings or vectors of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of ''substitutions'' required to change one string into the other, or equivalently, the minimum number of ''errors'' that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming. A major application is in coding theory, more specifically to block codes, in which the equal-length strings are Vector space, vectors over a finite field. Definition The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different. Examples The symbols may be letters, bits, or decimal digits, am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Code Rate
In telecommunication and information theory, the code rate (or information rateHuffman, W. Cary, and Pless, Vera, ''Fundamentals of Error-Correcting Codes'', Cambridge, 2003.) of a forward error correction code is the proportion of the data-stream that is useful (non- redundant). That is, if the code rate is k/n for every bits of useful information, the coder generates a total of bits of data, of which n-k are redundant. If is the gross bit rate or data signalling rate (inclusive of redundant error coding), the net bit rate (the useful bit rate exclusive of error correction codes) is \leq R \cdot k/n. For example: The code rate of a convolutional code will typically be , , , , , etc., corresponding to one redundant bit inserted after every single, second, third, etc., bit. The code rate of the octet oriented Reed Solomon block code denoted RS(204,188) is 188/204, meaning that redundant octets (or bytes) are added to each block of 188 octets of useful information. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ASCII
ASCII ( ), an acronym for American Standard Code for Information Interchange, is a character encoding standard for representing a particular set of 95 (English language focused) printable character, printable and 33 control character, control characters a total of 128 code points. The set of available punctuation had significant impact on the syntax of computer languages and text markup. ASCII hugely influenced the design of character sets used by modern computers; for example, the first 128 code points of Unicode are the same as ASCII. ASCII encodes each code-point as a value from 0 to 127 storable as a seven-bit integer. Ninety-five code-points are printable, including digits ''0'' to ''9'', lowercase letters ''a'' to ''z'', uppercase letters ''A'' to ''Z'', and commonly used punctuation symbols. For example, the letter is represented as 105 (decimal). Also, ASCII specifies 33 non-printing control codes which originated with ; most of which are now obsolete. The control cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nomenclature
Nomenclature (, ) is a system of names or terms, or the rules for forming these terms in a particular field of arts or sciences. (The theoretical field studying nomenclature is sometimes referred to as ''onymology'' or ''taxonymy'' ). The principles of naming vary from the relatively informal conventions of everyday speech to the internationally agreed principles, rules, and recommendations that govern the formation and use of the specialist terminology used in scientific and any other disciplines. Naming "things" is a part of general human communication using words and language: it is an aspect of everyday taxonomy as people distinguish the objects of their experience, together with their similarities and differences, which observers identify, name and classify. The use of names, as the many different kinds of nouns embedded in different languages, connects nomenclature to theoretical linguistics, while the way humans mentally structure the world in relation to word meanings a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repetition Code
In coding theory, the repetition code is one of the most basic linear error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel corrupts only a minority of these repetitions. This way the receiver will notice that a transmission error occurred since the received data stream is not the repetition of a single message, and moreover, the receiver can recover the original message by looking at the received message in the data stream that occurs most often. Because of the bad error correcting performance coupled with the low code rate (ratio between useful information symbols and actual transmitted symbols), other error correction codes are preferred in most cases. The chief attraction of the repetition code is the ease of implementation. Code parameters In the case of a binary repetition code, there exist two co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is divisible by 2, and odd if it is not.. For example, −4, 0, and 82 are even numbers, while −3, 5, 23, and 69 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers with decimals or fractions like 1/2 or 4.6978. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwise it is even—as the last digit of any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Even Number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is divisible by 2, and odd if it is not.. For example, −4, 0, and 82 are even numbers, while −3, 5, 23, and 69 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers with decimals or fractions like 1/2 or 4.6978. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwise it is even—as the last digit of any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Punched Paper Tape
Punch commonly refers to: * Punch (combat), a strike made using the hand closed into a fist * Punch (drink), a wide assortment of drinks, non-alcoholic or alcoholic, generally containing fruit or fruit juice Punch may also refer to: Places * Punch, U.S. Virgin Islands * Poonch (other), often spelt as Punch, several places in India and Pakistan People * Punch (surname), a list of people with the name * Punch (nickname), a list of people with the nickname * Punch Masenamela (born 1986), South African footballer * Punch (rapper), 21st century American rapper Terrence Louis Henderson Jr. * Punch (singer), South Korean singer Bae Jin-young (born 1993) Arts, entertainment and media Fictional entities * Mr. Punch (also known as Pulcinella or Pulcinello), the principal puppet character in the traditional ''Punch and Judy'' puppet show * Mr. Punch, the masthead image and nominal editor of '' Punch'', largely borrowed from the puppet show * Mr. Punch, a fictional charact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromechanical
Electromechanics combine processes and procedures drawn from electrical engineering and mechanical engineering. Electromechanics focus on the interaction of electrical and mechanical systems as a whole and how the two systems interact with each other. This process is especially prominent in systems such as those of DC or AC rotating electrical machines which can be designed and operated to generate power from a mechanical process ( generator) or used to power a mechanical effect ( motor). Electrical engineering in this context also encompasses electronics engineering. Electromechanical devices are ones which have both electrical and mechanical processes. Strictly speaking, a manually operated switch is an electromechanical component due to the mechanical movement causing an electrical output. Though this is true, the term is usually understood to refer to devices which involve an electrical signal to create mechanical movement, or vice versa mechanical movement to create an ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |