|
Hilbert Basis
Hilbert basis may refer to * In Invariant theory, a finite set of invariant polynomials, such that every invariant polynomial may be written as a polynomial function of these basis elements * Orthonormal basis of a Hilbert space * Hilbert basis (linear programming) The Hilbert basis of a convex cone ''C'' is a minimal set of integer vectors such that every integer vector in ''C'' is a conical combination of the vectors in the Hilbert basis with integer coefficients. Definition Given a lattice L\subset\ma ... * Hilbert's basis theorem {{mathdab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties, such as vector spaces, from the point of view of their effect on functions. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are ''invariant'', under the transformations from a given linear group. For example, if we consider the action of the special linear group ''SLn'' on the space of ''n'' by ''n'' matrices by left multiplication, then the determinant is an invariant of this action because the determinant of ''A X'' equals the determinant of ''X'', when ''A'' is in ''SLn''. Introduction Let G be a group, and V a finite-dimensional vector space over a field k (which in classical invariant theory was usually assumed to be the complex numbers). A representation of G in V is a group homomorphism \pi:G \to GL(V), which induces a group action of G on V. If k /math> is the space of polynomial functions on V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space ''V'' with finite dimension is a basis for V whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The image of the standard basis under a rotation or reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. For a general inner product space V, an orthonormal basis can be used to define normalized orthogonal coordinates on V. Under these coordinates, the inner product becomes a dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional inner product space to the study of \R^n under dot product. Every finite-dimensional inner product space has an orthonormal basis, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
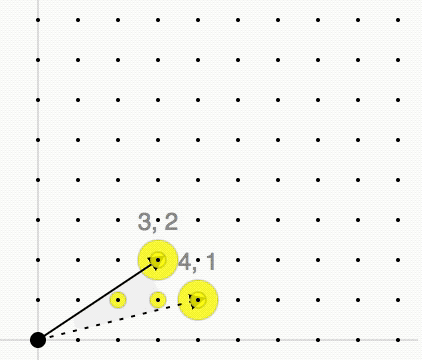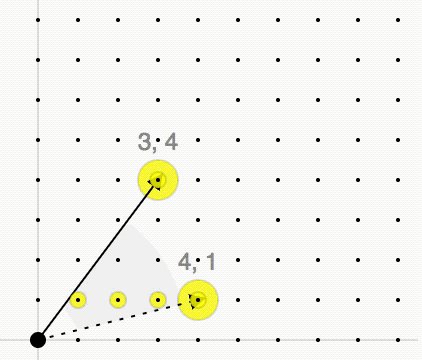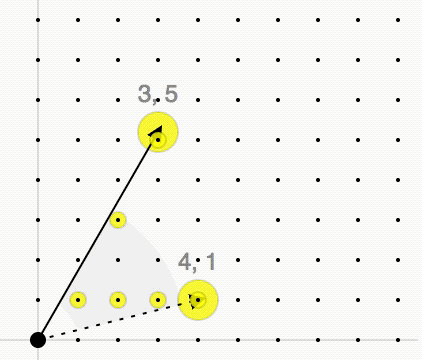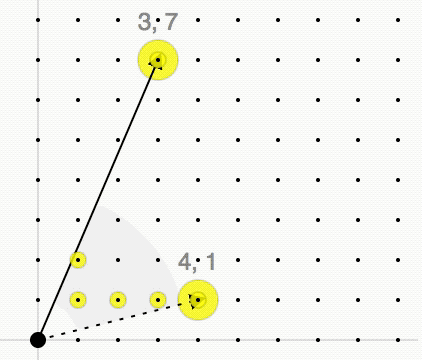
Hilbert Basis (linear Programming)
The Hilbert basis of a convex cone ''C'' is a minimal set of integer vectors such that every integer vector in ''C'' is a conical combination of the vectors in the Hilbert basis with integer coefficients. Definition Given a lattice L\subset\mathbb^d and a convex polyhedral cone with generators a_1,\ldots,a_n\in\mathbb^d :C=\\subset\mathbb^d we consider the monoid In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0. Monoids ... C\cap L. By Gordan's lemma this monoid is finitely generated, i.e., there exists a finite set of lattice points \\subset C\cap L such that every lattice point x\in C\cap L is an integer conical combination of these points: : x=\lambda_1 x_1+\ldots+\lambda_m x_m, \quad\lambda_1,\ldots,\lambda_m\in\mathbb, \lambda_1,\ldots,\lambda_m\geq0 The cone ''C'' is called poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |