Hilbert basis (linear programming) on:
[Wikipedia]
[Google]
[Amazon]
The Hilbert basis of a
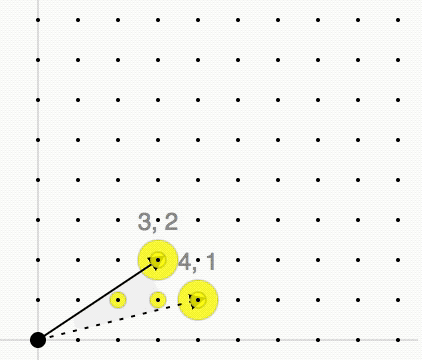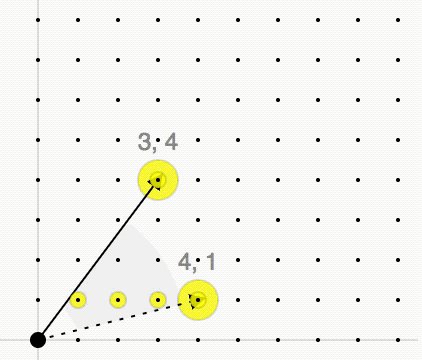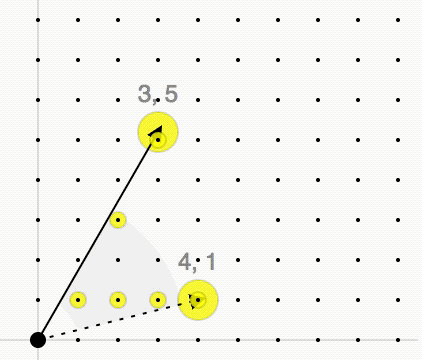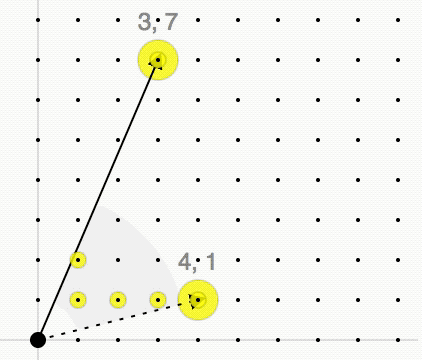 Given a lattice and a convex polyhedral cone with generators
:
we consider the
Given a lattice and a convex polyhedral cone with generators
:
we consider the
convex cone
In linear algebra, a cone—sometimes called a linear cone to distinguish it from other sorts of cones—is a subset of a real vector space that is closed under positive scalar multiplication; that is, C is a cone if x\in C implies sx\in C for e ...
''C'' is a minimal set of integer vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
s in ''C'' such that every integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
vector in ''C'' is a conical combination of the vectors in the Hilbert basis with integer coefficients.
Definition
 Given a lattice and a convex polyhedral cone with generators
:
we consider the
Given a lattice and a convex polyhedral cone with generators
:
we consider the monoid
In abstract algebra, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being .
Monoids are semigroups with identity ...
. By Gordan's lemma, this monoid is finitely generated, i.e., there exists a finite set
In mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
is a finite set with five elements. Th ...
of lattice points such that every lattice point is an integer conical combination of these points:
:
The cone ''C'' is called pointed if implies . In this case there exists a unique minimal generating set of the monoid —the Hilbert basis of ''C''. It is given by the set of irreducible lattice points: An element is called irreducible if it can not be written as the sum of two non-zero elements, i.e., implies or .
References
* * * * Linear programming Discrete geometry Eponyms in geometry {{mathapplied-stub