|
Exponential Tree
An exponential tree is a type of search tree In computer science, a search tree is a tree data structure used for locating specific keys from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left, and les ... where the number of children of its nodes decreases doubly- exponentially with increasing depth. Values are stored only in the leaf nodes. Each node contains a splitter, a value less than or equal to all values in the subtree which is used during search. Exponential trees use another data structure in inner nodes containing the splitters from children, allowing fast lookup. Exponential trees achieve optimal asymptotic complexity on some operations. They have mainly theoretical importance. Tree structure An exponential tree is a rooted tree where every node contains a splitter and every leaf node contains a value. The value may be different from the splitter. An exponential tree with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Search Tree
In computer science, a search tree is a tree data structure used for locating specific keys from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left, and less than any keys in subtrees on the right. The advantage of search trees is their efficient search time given the tree is reasonably balanced, which is to say the leaves at either end are of comparable depths. Various search-tree data structures exist, several of which also allow efficient insertion and deletion of elements, which operations then have to maintain tree balance. Search trees are often used to implement an associative array. The search tree algorithm uses the key from the key–value pair to find a location, and then the application stores the entire key–value pair at that particular location. Types of trees Binary search tree A Binary Search Tree is a node-based data structure where each node contains a key and two su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rooted Tree
In graph theory, a tree is an undirected graph in which any two vertices are connected by path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A directed tree, oriented tree,See .See . polytree,See . or singly connected networkSee . is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is called an arborescence or out-tree� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
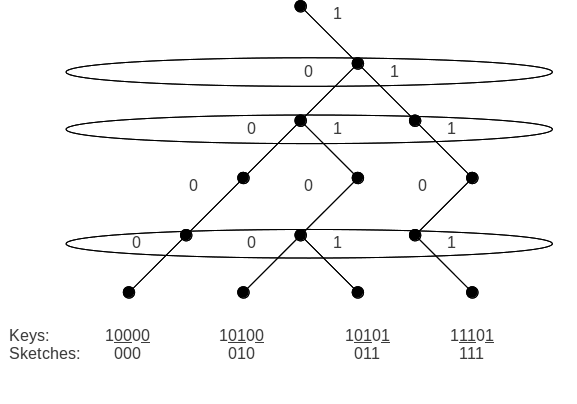 |
Fusion Tree
In computer science, a fusion tree is a type of tree data structure that implements an associative array on -bit integers on a finite universe, where each of the input integers has size less than 2w and is non-negative. When operating on a collection of Attribute–value pair, key–value pairs, it uses space and performs searches in time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of . It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard. Several advances have been made since Fredman and Willard's original 1990 paper. In 1999. it was shown how to implement fusion trees under a model of computation in which all of the underlying operations of the algorithm belong to AC0, AC0, a model of circuit complexity that allows addition and bitwise Boolean operations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |