Fusion Tree

In computer science, a fusion tree is a type of tree data structure that implements an associative array on -bit integers on a finite universe, where each of the input integers has size less than 2^w and is non-negative. When operating on a collection of key–value pairs, it uses space and performs searches in time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of . It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard.

Several advances have been made since Fredman and Willard's original 1990 paper. In 1999. it was shown how to implement fusion trees under a model of computation in which all of the underlying operations of the algorithm belong to AC⁰, a model of circuit complexity that allows addition and bitwise Boolean operations but does not allow the multiplication operations used in the original fusion tree algorithm. A dynamic version of fusion trees using hash tables was proposed in 1996 which matched the original structure's runtime in expectation. Another dynamic version using exponential tree was proposed in 2007 which yields worst-case runtimes of per operation. Finally, it was shown that dynamic fusion trees can perform each operation in time deterministically.

This data structure implements add key, remove key, search key, and predecessor (next smaller value) and successor (next larger value) search operations for a given key. The partial result of most significant bit locator in constant time has also helped further research. Fusion trees utilize word-level parallelism to be efficient, performing computation on several small integers, stored in a single machine word, simultaneously to reduce the number of total operations.

How it works

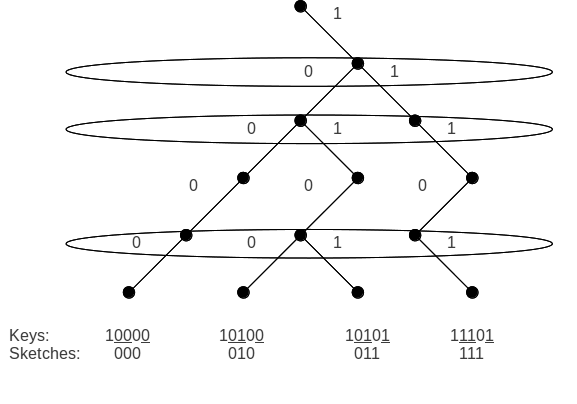
A fusion tree is essentially a B-tree with branching factor of (any small exponent is also possible as it will not have a great impact on the height of the tree), which gives it a height of . To achieve the desired runtimes for updates and queries, the fusion tree must be able to search a node containing up to keys in constant time. This is done by compressing ("sketching") the keys so that all can fit into one machine word, which in turn allows comparisons to be done in parallel. So, a series of computations involving sketching, parallel comparison and most significant bit index locator, help reach the required solution.

Sketching

Sketching is the method by which each -bit key at a node containing keys is compressed into only bits. Each key may be thought of as a path in the full binary tree of height starting at the root and ending at the leaf corresponding to . This path can be processed by recursively searching the left child of ''i'' if the ''ith'' bit is 0, and the right child if it is 1, generally, until all bits are scanned. To distinguish two paths, it suffices to look at their branching point (the first bit where any two keys differ). As there are a maximum of ''k'' keys, there will not be more than ''k-1'' branching points, which means that no more than ''k-1'' bits are required to identify a key. And hence, no sketch will have more than ''k-1'' bits.

An important property of the sketch function is that it preserves the order of the keys. That is, for any two keys . So, for the entire range of keys, sketch(x₀)1)<...k-1) because if the binary-tree-like path is followed, the nodes will be ordered in such a manner that x₀1<...k-1.

Approximating the sketch

If the locations of the sketch bits are ''b''₁ < ''b''₂ < ⋅⋅⋅ < ''b''_''r'', then the sketch of the key ''x''_''w''-1⋅⋅⋅''x''₁''x''₀ is the ''r''-bit integer $x_x_\cdots x_$.

With only standard word operations, such as those of the C programming language, it is difficult to directly compute the perfect sketch of a key in constant time. Instead, the sketch bits can be packed into a range of size at most ''r''⁴, using bitwise AND and multiplication, called the approximate sketch, which does have all the important bits but also some additional useless bits spread out in a predictable pattern. The bitwise AND operation serves as a mask to remove all these non-sketch bits from the key, while the multiplication shifts the sketch bits into a small range. Like the "perfect" sketch, the approximate sketch also preserves the order of the keys and means that sketch(x₀)1)<...k-1).

Some preprocessing is needed to determine the correct multiplication constant. Each sketch bit in location ''b''_''i'' will get shifted to ''b''_''i'' + ''m''_''i'' via a multiplication by ''m'' = $\textstyle\sum_^r$ 2^''m''_''i''. For the approximate sketch to work, the following three properties must hold:

# ''b''_''i'' + ''m''_''j'' are distinct for all pairs (''i'', ''j''). This will ensure that the sketch bits are uncorrupted by the multiplication.
# ''b''_''i'' + ''m''_''i'' is a strictly increasing function of ''i''. That is, the order of the sketch bits is preserved even in x'.m.
# (''b''_''r'' + ''m''_''r'') - (''b''₁ + ''m''₁) ≤ ''r''⁴. That is, the sketch bits are packed into a range of size at most ''r''⁴, where r ≤ O(w^1/5).

An inductive argument shows how the ''m''_''i'' can be constructed. Let ''m''₁ = ''w'' − ''b''₁. Suppose that 1 < ''t'' ≤ ''r'' and that ''m''₁, ''m''₂... ''m''_''t-1'' have already been chosen. Then pick the smallest integer ''m''_''t'' such that both properties (1) and (2) are satisfied. Property (1) requires that ''m''_''t'' ≠ ''b''_''i'' − ''b''_''j'' + ''m''_''l'' for all 1 ≤ ''i'', ''j'' ≤ ''r'' and 1 ≤ ''l'' ≤ ''t''-1. Thus, there are less than ''tr''² ≤ ''r''³ values that ''m''_''t'' must avoid. Since ''m''_''t'' is chosen to be minimal, (''b''_''t'' + ''m''_''t'') ≤ (''b''_''t''-1 + ''m''_''t''-1) + ''r''³. This implies Property (3).

The approximate sketch is thus computed as follows:
# Mask out all but the sketch bits with a bitwise AND between ''x'' and $\sum_^ 2^$.
# Multiply the key by the predetermined constant ''m'' as calculated above. This operation actually requires two machine words, but this can still be done in constant time.
# Mask out all but the shifted sketch bits. These are now contained in a contiguous block of at most ''r''⁴ < ''w''^4/5 bits.

Parallel comparison

The purpose of the compression achieved by sketching is to allow all of the keys to be stored in one ''w''-bit word. Let the ''node sketch'' of a node be the bit string

:1sketch(''x''₁)1sketch(''x''₂)...1sketch(''x''_''k'')

Here, all sketch words are clubbed together in one string by prepending a set bit to each of them. We can assume that the sketch function uses exactly ''b'' ≤ ''r''⁴ bits. Then each block uses 1 + ''b'' ≤ ''w''^4/5 bits, and since ''k'' ≤ ''w''^1/5, the total number of bits in the node sketch is at most ''w''.

A brief notational aside: for a bit string ''s'' and nonnegative integer ''m'', let ''s''^''m'' denote the concatenation of ''s'' to itself ''m'' times. If ''t'' is also a bit string, ''st'' denotes the concatenation of ''t'' to ''s''.

The node sketch makes it possible to search the keys for any ''b''-bit integer ''y''. Let ''z'' = (0''y'')^''k'', which can be computed in constant time (multiply ''y'' by the constant (0^''b''1)^''k''), to make it as long as the node sketch such that each word in the node sketch can be compared with the query integer ''y'' in one operation, demonstrating word-level parallelism. If ''y'' were 5 bits long, it would be multiplied by 000001....000001 to get sketch(y)^k. The difference between sketch(x_i) and 0y results in the leading bit for each block to be 1, if and only if sketch(y) $\leq$ sketch(x_i). We can thus compute the smallest index ''i'' such that sketch(''x''_''i'') ≥ ''y'' as follows:

# Subtract ''z'' from the node sketch.
# Take the bitwise AND of the difference and the constant (10^''b'')^''k''. This clears all but the leading bit of each block.
# Find the most significant bit of the result, to identify the exact index of transition from elements with sketch smaller than the query sketch to those greater than the query sketch.
# Compute ''i,'' the rank of the sketch, using the fact that the leading bit of the ''i''-th block has index ''i''(''b''+1).

Desketching

For an arbitrary query ''q'', parallel comparison computes the index ''i'' such that
:sketch(''x''_''i''-1) ≤ sketch(''q'') ≤ sketch(''x''_''i'')
Unfortunately, this does give the exact predecessor or successor of ''q'', because the location of the sketch of ''q'' among the sketches of all the values may not be the same as the location of ''q'' in all the actual values. What is true is that, among all of the keys, either ''x''_''i''-1 or ''x''_''i'' has the longest common prefix with ''q''. This is because any key ''y'' with a longer common prefix with ''q'' would also have more sketch bits in common with ''q'', and thus sketch(''y'') would be closer to sketch(''q'') than any sketch(''x''_''j'').

The length longest common prefix between two ''w''-bit integers ''a'' and ''b'' can be computed in constant time by finding the most significant bit of the bitwise XOR between ''a'' and ''b''. This can then be used to mask out all but the longest common prefix.

Note that ''p'' identifies exactly where ''q'' branches off from the set of keys. If the next bit of ''q'' is 0, then the successor of ''q'' is contained in the ''p''1 subtree, and if the next bit of ''q'' is 1, then the predecessor of ''q'' is contained in the ''p''0 subtree. This suggests the following algorithm for determining the exact location of ''q'':

# Use parallel comparison to find the index ''i'' such that sketch(''x''_''i''-1) ≤ sketch(''q'') ≤ sketch(''x''_''i'').
# Compute the longest common prefix ''p'' of ''q'' and either ''x''_''i''-1 or ''x''_''i'' (taking the longer of the two).
# Let ''l''-1 be the length of the longest common prefix ''p''.
## If the ''l''-th bit of ''q'' is 0, let ''e'' = ''p''10^''w''-''l''. Use parallel comparison to search for the successor of sketch(''e''). This is the actual predecessor of ''q''.
## If the ''l''-th bit of ''q'' is 1, let ''e'' = ''p''01^''w''-''l''. Use parallel comparison to search for the predecessor of sketch(''e''). This is the actual successor of ''q''.
# Once either the predecessor or successor of ''q'' is found, the exact position of ''q'' among the set of keys is determined.

Fusion hashing

An application of fusion trees to hash tables was given by Willard, who describes a data structure for hashing in which an outer-level hash table with hash chaining is combined with a fusion tree representing each hash chain.
In hash chaining, in a hash table with a constant load factor, the average size of a chain is constant, but additionally with high probability all chains have size , where is the number of hashed items.
This chain size is small enough that a fusion tree can handle searches and updates within it in constant time per operation. Therefore, the time for all operations in the data structure is constant with high probability.
More precisely, with this data structure, for every inverse- quasipolynomial probability , there is a constant such that the probability that there exists an operation that exceeds time is at most .

Computational Model and Necessary Assumptions

The computational model for the Fusion Tree algorithm is a Word RAM with a specific instruction set, including arithmetic instructions - addition, subtraction and multiplication (all performed
modulo ) and Boolean operations - bitwise AND, NOT etc. A double-precision multiplication instruction is also included. It has been shown. that removal of the latter instruction makes it impossible to sort faster than , unless it is permitted to use memory space of nearly words (in contrast to linear space used by Fusion Trees), or include other instructions instead.

References

External links

MIT CS 6.897: Advanced Data Structures: Lecture 4, Fusion Trees
Prof. Erik Demaine (Spring 2003)

MIT CS 6.897: Advanced Data Structures: Lecture 5, More fusion trees; self-organizing data structures, move-to-front, static optimality
Prof. Erik Demaine (Spring 2003)

MIT CS 6.851: Advanced Data Structures: Lecture 13, Fusion Tree notes
Prof. Erik Demaine (Spring 2007)

MIT CS 6.851: Advanced Data Structures: Lecture 12, Fusion Tree notes
Prof. Erik Demaine (Spring 2012)

{{CS-Trees

Trees (data structures)
Associative arrays