|
Dissection Puzzle
A dissection puzzle, also called a transformation puzzle or Richter puzzle, is a tiling puzzle where a set of pieces can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of dissection puzzle. Puzzles may include various restraints, such as hinged pieces, pieces that can fold, or pieces that can twist. Creators of new dissection puzzles emphasize using a minimum number of pieces, or creating novel situations, such as ensuring that every piece connects to another with a hinge. History Dissection puzzles are an early form of geometric puzzle. The earliest known descriptions of dissection puzzles are from the time of Plato (427–347 BCE) in Ancient Greece, and involve the challenge of turning two equal squares into one larger square using four pieces. Other ancient dissection puzzles were used as graphic depictions of the Pythagorean theorem (see square trisection). A fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tiling Puzzle
Tiling puzzles are puzzles involving two-dimensional packing problems in which a number of flat shapes have to be assembled into a larger given shape without overlaps (and often without gaps). Some tiling puzzles ask players to dissect a given shape first and then rearrange the pieces into another shape. Other tiling puzzles ask players to dissect a given shape while fulfilling certain conditions. The two latter types of tiling puzzles are also called dissection puzzles. Tiling puzzles may be made from wood, metal, cardboard, plastic or any other sheet-material. Many tiling puzzles are now available as computer games. Tiling puzzles have a long history. Some of the oldest and most famous are jigsaw puzzles and the tangram puzzle. Other examples of tiling puzzles include: * Conway puzzle * Domino tiling, of which the mutilated chessboard problem is one example * Eternity puzzle * Geometric magic square * Puzz-3D * Squaring the square * Tantrix * T puzzle Many ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Games Column
Over a period of 24 years (January 1957 – December 1980), Martin Gardner wrote 288 consecutive monthly "Mathematical Games" columns for ''Scientific American'' magazine. During the next years, until June 1986, Gardner wrote 9 more columns, bringing his total to 297. During this period other authors wrote most of the columns. In 1981, Gardner's column alternated with a new column by Douglas Hofstadter called " Metamagical Themas" (an anagram of "Mathematical Games"). The table below lists Gardner's columns. Twelve of Gardner's columns provided the cover art for that month's magazine, indicated by " over in the table with a hyperlink to the cover. Other articles by Gardner Gardner wrote 5 other articles for ''Scientific American''. His flexagon article in December 1956 was in all but name the first article in the series of ''Mathematical Games'' columns and led directly to the series which began the following month. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A K Peters
A K Peters, Ltd. was a publisher of scientific and technical books, specializing in mathematics and in computer graphics, robotics, and other fields of computer science. They published the journals '' Experimental Mathematics'' and the '' Journal of Graphics Tools'', as well as mathematics books geared to children. Background Klaus Peters wrote a doctoral dissertation on complex manifolds at the University of Erlangen in 1962, supervised by Reinhold Remmert. He then joined Springer Verlag, becoming their first specialist mathematics editor. As a Springer director from 1971, he hired Alice Merker for Springer New York: they were married that year, and moved to Heidelberg. Leaving Springer, they founded Birkhäuser Boston in 1979; Birkhäuser ran into financial difficulties, and was taken over by Springer. Klaus and Alice then spent a period running a Boston office for Harcourt Brace Jovanovich and their imprint Academic Press. With the takeover of Harcourt Brace Jovanovich by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangram
The tangram () is a dissection puzzle consisting of seven flat polygons, called ''tans'', which are put together to form shapes. The objective is to replicate a pattern (given only an outline) generally found in a puzzle book using all seven pieces without overlap. Alternatively the ''tans'' can be used to create original minimalist designs that are either appreciated for their inherent aesthetic merits or as the basis for challenging others to replicate its outline. It is reputed to have been invented in China sometime around the late 18th century and then carried over to America and Europe by trading ships shortly after. It became very popular in Europe for a time, and then again during World War I. It is one of the most widely recognized dissection puzzles in the world and has been used for various purposes including amusement, art, and education. Etymology The origin of the English word 'tangram' is unclear. One conjecture holds that it is a compound of the Greek element ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vanishing Puzzle
A vanishing puzzle is a mechanical puzzle, mechanical optical illusion comprising multiple pieces which can be rearranged to show different versions of a picture depicting several objects, the number of which depending on the arrangement of the pieces. History Wemple & Company marketed an advertising card named ''The Magic Egg Puzzle, (How Many Eggs?)'' in New York in 1880. Cutting the rectangular card into four oblongs allowed the pieces to be rearranged to show either 8, 9 or 10 eggs. Many other similar puzzles have been published since. Chess player and recreational mathematician Sam Loyd patented rotary vanishing puzzles in 1896 and published versions named ''Get Off the Earth'', ''Teddy and the Lion'' and ''The Disappearing Bicyclist'' (pictured). Each had a circular card connected to a cardboard backdrop with a pin, letting it freely rotate. In ''The Disappearing Bicyclist'', when the disc is rotated such that the arrow points to A, 13 boys can be counted, but when i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusion
In visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual perception, percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immersed in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo illusion, Ponzo, Poggendorff illusion, Poggendorff, and M� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
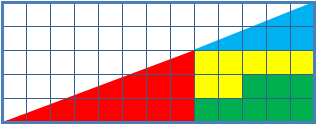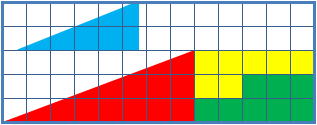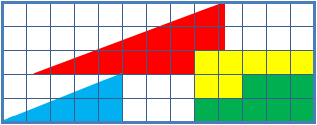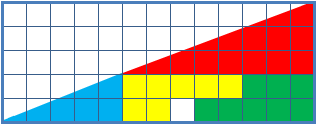
Missing Square Puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ArXiv
arXiv (pronounced as "archive"—the X represents the Chi (letter), Greek letter chi ⟨χ⟩) is an open-access repository of electronic preprints and postprints (known as e-prints) approved for posting after moderation, but not Scholarly peer review, peer reviewed. It consists of scientific papers in the fields of mathematics, physics, astronomy, electrical engineering, computer science, quantitative biology, statistics, mathematical finance, and economics, which can be accessed online. In many fields of mathematics and physics, almost all scientific papers are self-archiving, self-archived on the arXiv repository before publication in a peer-reviewed journal. Some publishers also grant permission for authors to archive the peer-reviewed postprint. Begun on August 14, 1991, arXiv.org passed the half-million-article milestone on October 3, 2008, had hit a million by the end of 2014 and two million by the end of 2021. As of November 2024, the submission rate is about 24,000 arti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erik Demaine
Erik D. Demaine (born February 28, 1981) is a Canadian-American professor of computer science at the Massachusetts Institute of Technology and a former child prodigy. Early life and education Demaine was born in Halifax, Nova Scotia, to mathematician and sculptor Martin L. Demaine and Judy Anderson. From the age of 7, he was identified as a child prodigy and spent time traveling across North America with his father. He was home-schooled during that time span until entering university at the age of 12. Demaine completed his bachelor's degree at 14 years of age at Dalhousie University in Canada, and completed his PhD at the University of Waterloo by the time he was 20 years old. Demaine's PhD dissertation, a work in the field of computational origami, was completed at the University of Waterloo under the supervision of Anna Lubiw and Ian Munro. This work was awarded the Canadian Governor General's Gold Medal from the University of Waterloo and the NSERC Doctoral Prize (200 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |