Missing square puzzle

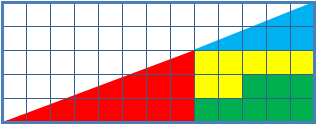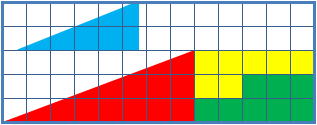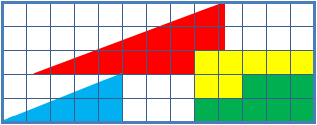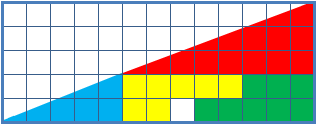
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it.

Solution

The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye.

A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears that the area should be ''S'' = = 32.5 units. However, the blue triangle has a ratio of 5:2 (=2.5), while the red triangle has the ratio 8:3 (≈2.667), so the apparent combined hypotenuse in each figure is actually bent. With the bent hypotenuse, the first figure actually occupies a combined 32 units, while the second figure occupies 33, including the "missing" square.

The amount of bending is approximately units (1.245364267°), which is difficult to see on the diagram of the puzzle, and was illustrated as a graphic. Note the grid point where the red and blue triangles in the lower image meet (5 squares to the right and two units up from the lower left corner of the combined figure), and compare it to the same point on the other figure; the edge is slightly under the mark in the upper image, but goes through it in the lower. Overlaying the "hypotenuses" from both figures results in a very thin parallelogram (represented with the four red dots in the above image) with an area of exactly one grid square ( Pick's theorem gives 0 + − 1 = 1), which corresponds to the "missing" area.

Principle

According to Martin Gardner, this particular puzzle was invented by a New York City amateur magician, Paul Curry, in 1953. However, the principle of a dissection paradox has been known since the start of the 16th century.

The integer dimensions of the parts of the puzzle (2, 3, 5, 8, 13) are successive Fibonacci numbers, which leads to the exact unit area in the ''thin parallelogram''.
Many other geometric dissection puzzles are based on a few simple properties of the Fibonacci sequence.

Similar puzzles

Sam Loyd's chessboard paradox demonstrates two rearrangements of an 8×8 square. In the "larger" rearrangement (the 5×13 rectangle in the image to the right), the gaps between the figures have a combined unit square more area than their square gaps counterparts, creating an illusion that the figures there take up more space than those in the original square figure. In the "smaller" rearrangement (the shape below the 5×13 rectangle), each quadrilateral needs to overlap the triangle by an area of half a unit for its top/bottom edge to align with a grid line, resulting overall loss in one unit square area.

Mitsunobu Matsuyama's paradox uses four congruent quadrilaterals and a small square, which form a larger square. When the quadrilaterals are rotated about their centers they fill the space of the small square, although the total area of the figure seems unchanged. The apparent paradox is explained by the fact that the side of the new large square is a little smaller than the original one. If ''θ'' is the angle between two opposing sides in each quadrilateral, then the ratio of the two areas is given by sec² ''θ''. For ''θ'' = 5°, this is approximately 1.00765, which corresponds to a difference of about 0.8%.

A vanishing puzzle is a mechanical optical illusion showing different numbers of a certain object when parts of the puzzle are moved around.The Guardian
''Vanishing Leprechaun, Disappearing Dwarf and Swinging Sixties Pin-up Girls – puzzles in pictures''
/ref>

See also

*
*
*
*

References

External links

*A printabl

with a video demonstration.
Curry's Paradox: How Is It Possible?
at cut-the-knot
Jigsaw ParadoxThe Eleven Holes Puzzle"Infinite Chocolate Bar Trick"
a demonstration of the missing square puzzle utilising a 4×6 chocolate bar
{{DEFAULTSORT:Missing Square Puzzle
Optical illusions
Fibonacci numbers
Elementary mathematics
Mathematical paradoxes
Recreational mathematics
Geometric dissection