|
Chazelle Polyhedron
Chazelle polyhedron is a non-convex polyhedron constructed by removing pieces of wedges from both top and bottom of a cube's sides, leaving the notches. Its saddle surface can be considered as the set of line segments that lie forming the hyperbolic paraboloid with an equation z = xy. This polyhedron is named after Bernard Chazelle. Originally, the Chazelle polyhedron was intended to prove the quadratic lower bound of complexity on the decomposition of convex polyhedra in three dimensions. The later applications are used regarding the problem related to the construction of lower bounds as in the binary space partition, bounding volume hierarchy for collision detection, decomposability of fat-polyhedra, and optimal triangulation in mesh generation Mesh generation is the practice of creating a polygon mesh, mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partitio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
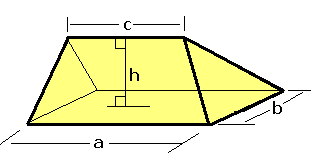
Wedge (geometry)
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices. Properties A wedge is a polyhedron of a rectangular base, with the faces are two Isosceles triangle, isosceles triangles and two trapezoids that meet at the top of an edge.. A prismatoid is defined as a polyhedron where its vertices lie on two parallel planes, with its lateral faces are triangles, Trapezoid, trapezoids, and Parallelogram, parallelograms; the wedge is an example of prismatoid because of its top edge is parallel to the rectangular base. The volume of a wedge is V = bh \left(\frac+\frac\right), where the base rectangle is a by b , c is the Apex (geometry), apex edge length parallel to a , and h is the height from the base rectangle to the apex edge. Examples In some special cases, the wedge is the right prism if all edges connecting triangles are equal in length, and the triangular faces are perpendicula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Surface
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface that ''curves up'' in one direction, and ''curves down'' in a different direction, resembling a riding saddle. In terms of contour lines, a saddle point in two dimensions gives rise to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid made by a plane parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The paraboloid is hyperbolic if the factors are real; elliptic if the factors are complex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernard Chazelle
Bernard Chazelle (born November 5, 1955) is a French computer scientist. He is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he is known for his study of algorithms, such as linear-time triangulation of a simple polygon, as well as major complexity results, such as lower bound techniques based on discrepancy theory. He is also known for his invention of the soft heap data structure and the most asymptotically efficient known deterministic algorithm for finding minimum spanning trees. Early life Chazelle was born in Clamart, France, the son of Marie-Claire (née Blanc) and Jean Chazelle. He grew up in Paris, France, where he received his bachelor's degree and master's degree in applied mathematics at the École des mines de Paris in 1977. Then, at the age of 21, he attended Yale University in the United States, where he received his PhD in computer science in 1980 under the supervision of David ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Space Partition
In computer science, binary space partitioning (BSP) is a method for space partitioning which recursively subdivides a Euclidean space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to a representation of objects within the space in the form of a tree data structure known as a BSP tree. Binary space partitioning was developed in the context of 3D computer graphics in 1969. The structure of a BSP tree is useful in rendering because it can efficiently give spatial information about the objects in a scene, such as objects being ordered from front-to-back with respect to a viewer at a given location. Other applications of BSP include: performing geometrical operations with shapes ( constructive solid geometry) in CAD, collision detection in robotics and 3D video games, ray tracing, virtual landscape simulation, and other applications that involve the handling of complex spatial scenes. History *1969 Schumacker et al. published a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounding Volume Hierarchy
A bounding volume hierarchy (BVH) is a tree structure on a set of geometric objects. All geometric objects, which form the leaf nodes of the tree, are wrapped in bounding volumes. These nodes are then grouped as small sets and enclosed within larger bounding volumes. These, in turn, are also grouped and enclosed within other larger bounding volumes in a recursive fashion, eventually resulting in a tree structure with a single bounding volume at the top of the tree. Bounding volume hierarchies are used to support several operations on sets of geometric objects efficiently, such as in collision detection and ray tracing (graphics), ray tracing. Although wrapping objects in bounding volumes and performing collision tests on them before testing the object geometry itself simplifies the tests and can result in significant performance improvements, the same number of pairwise tests between bounding volumes are still being performed. By arranging the bounding volumes into a bounding volu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collision Detection
Collision detection is the computational problem of detecting an intersection of two or more objects in virtual space. More precisely, it deals with the questions of ''if'', ''when'' and ''where'' two or more objects intersect. Collision detection is a classic problem of computational geometry with applications in computer graphics, physical simulation, video games, robotics (including autonomous driving) and computational physics. Collision detection algorithms can be divided into operating on 2D or 3D spatial objects. Overview Collision detection is closely linked to calculating the distance between objects, as two objects (or more) intersect when the distance between them reaches zero or even becomes negative. Negative distance indicates that one object has penetrated another. Performing collision detection requires more context than just the distance between the objects. Accurately identifying the points of contact on both objects' surfaces is also essential for the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |