|
Bézier Surface
Bézier surfaces are a type of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive and, for many applications, mathematically convenient. History Bézier surfaces were first described in 1962 by the French engineer Pierre Bézier who used them to design automobile bodies. Bézier surfaces can be of any degree, but bicubic Bézier surfaces generally provide enough degrees of freedom for most applications. Equation A given Bézier surface of degree (''n'', ''m'') is defined by a set of (''n'' + 1)(''m'' + 1) control points k''i'',''j'' where ''i'' = 0, ..., ''n'' and ''j'' = 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spline (mathematics)
In mathematics, a spline is a function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees. In the computer science subfields of computer-aided design and computer graphics, the term ''spline'' more frequently refers to a piecewise polynomial ( parametric) curve. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design. The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes. Introduction The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rendering Pipeline
The computer graphics pipeline, also known as the rendering pipeline, or graphics pipeline, is a framework within computer graphics that outlines the necessary procedures for transforming a 3D computer graphics, three-dimensional (3D) scene into a 2D computer graphics, two-dimensional (2D) representation on a screen. Once a 3D model is generated, the graphics pipeline converts the model into a visually perceivable format on the computer display. Due to the dependence on specific software, Computer hardware, hardware configurations, and desired display attributes, a universally applicable graphics pipeline does not exist. Nevertheless, graphics API, application programming interfaces (APIs), such as Direct3D, OpenGL and Vulkan were developed to standardize common procedures and oversee the graphics pipeline of a given hardware accelerator. These APIs provide an abstraction layer over the underlying hardware, relieving programmers from the need to write code explicitly targeting vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ray Tracing (graphics)
In 3D computer graphics, ray tracing is a technique for modeling Light transport theory, light transport for use in a wide variety of Rendering (computer graphics), rendering algorithms for generating digital image, digital images. On a spectrum of Computation time, computational cost and visual fidelity, ray tracing-based rendering techniques, such as ray casting, #Recursive ray tracing algorithm, recursive ray tracing, Distributed ray tracing, distribution ray tracing, photon mapping and path tracing, are generally slower and higher fidelity than scanline rendering methods. Thus, ray tracing was first deployed in applications where taking a relatively long time to render could be tolerated, such as still computer-generated imagery, CGI images, and film and television visual effects (VFX), but was less suited to real-time computer graphics, real-time applications such as video games, where Frame rate, speed is critical in rendering each Film frame, frame. Since 2018, however, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cylinder (geometry)
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the '' right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bicubic Patches
In mathematics, bicubic interpolation is an extension of cubic spline interpolation (a method of applying cubic interpolation to a data set) for interpolating data points on a two-dimensional regular grid. The interpolated surface (meaning the kernel shape, not the image) is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation. Bicubic interpolation can be accomplished using either Lagrange polynomials, cubic splines, or cubic convolution algorithm. In image processing, bicubic interpolation is often chosen over bilinear or nearest-neighbor interpolation in image resampling, when speed is not an issue. In contrast to bilinear interpolation, which only takes 4 pixels (2×2) into account, bicubic interpolation considers 16 pixels (4×4). Images resampled with bicubic interpolation can have different interpolation artifacts, depending on the b and c values chosen. Computation Suppose the function values f and the derivat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
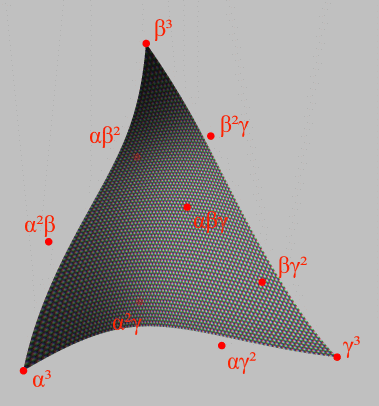
Bézier Triangle
A Bézier triangle is a special type of Bézier surface that is created by (Linearity, linear, Square (algebra), quadratic, Cube (algebra), cubic or higher degree) interpolation of control points. ''n''th-order Bézier triangle A general ''n''th-order Bézier triangle has (''n'' +1)(''n'' + 2)/2 Control point (mathematics), control points ''α''''i''''β''''j''''γ''''k'' where ''i'', ''j'', ''k'' are non-negative integers such that ''i'' + ''j'' + ''k'' = ''n''. The surface is then defined as : (\alpha s + \beta t + \gamma u)^n = \sum_ s^i t^j u^k \alpha^i \beta^j \gamma^k = \sum_ \frac s^i t^j u^k \alpha^i \beta^j \gamma^k for all non-negative real numbers ''s'' + ''t'' + ''u'' = 1. With Linearity, linear order (n=1), the resulting Bézier triangle is actually a regular flat triangle, with the triangle vertices equaling the three control points. A Square (algebra), quadratic (n=2) Bézier tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
B-spline
In numerical analysis, a B-spline (short for basis spline) is a type of Spline (mathematics), spline function designed to have minimal Support (mathematics), support (overlap) for a given Degree of a polynomial, degree, smoothness, and set of breakpoints (Knot (mathematics), knots that partition its Domain of a function, domain), making it a fundamental building block for all spline functions of that degree. A B-spline is defined as a piecewise polynomial of Order (mathematics), order n, meaning a degree of n - 1. It’s built from sections that meet at these knots, where the continuity of the function and its Derivative, derivatives depends on how often each knot repeats (its multiplicity). Any spline function of a specific degree can be uniquely expressed as a linear combination of B-splines of that degree over the same knots, a property that makes them versatile in mathematical modeling. A special subtype, cardinal B-splines, uses equidistant knots. The concept of B-splines tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
B-spline Surface
In numerical analysis, a B-spline (short for basis spline) is a type of spline function designed to have minimal support (overlap) for a given degree, smoothness, and set of breakpoints (knots that partition its domain), making it a fundamental building block for all spline functions of that degree. A B-spline is defined as a piecewise polynomial of order n, meaning a degree of n - 1. It’s built from sections that meet at these knots, where the continuity of the function and its derivatives depends on how often each knot repeats (its multiplicity). Any spline function of a specific degree can be uniquely expressed as a linear combination of B-splines of that degree over the same knots, a property that makes them versatile in mathematical modeling. A special subtype, cardinal B-splines, uses equidistant knots. The concept of B-splines traces back to the 19th century, when Nikolai Lobachevsky explored similar ideas at Kazan University in Russia, though the term "B-spline" wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |