|
Bid–ask Matrix
The bid–ask matrix is a matrix with elements corresponding with exchange rates between the assets. These rates are in ''physical units'' (e.g. number of stocks) and not with respect to any '' numeraire''. The (i,j) element of the matrix is the number of units of asset i which can be exchanged for 1 unit of asset j. Mathematical definition A d \times d matrix \Pi = \left pi_\right is a ''bid-ask matrix'', if # \pi_ > 0 for 1 \leq i,j \leq d. Any trade has a positive exchange rate. # \pi_ = 1 for 1 \leq i \leq d. Can always trade 1 unit with itself. # \pi_ \leq \pi_\pi_ for 1 \leq i,j,k \leq d. A direct exchange is always at most as expensive as a chain of exchanges. Example Assume a market with 2 assets (A and B), such that x units of A can be exchanged for 1 unit of B, and y units of B can be exchanged for 1 unit of A. Then the ''bid–ask matrix'' \Pi is: : \Pi = \begin 1 & x \\ y & 1 \end It is required that xy\ge1 by rule . With 3 assets, let a_ be the number of units ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Assets
In financial accounting, an asset is any resource owned or controlled by a business or an economic entity. It is anything (tangible or intangible) that can be used to produce positive economic value. Assets represent value of ownership that can be converted into cash (although cash itself is also considered an asset). The balance sheet of a firm records the monetaryThere are different methods of assessing the monetary value of the assets recorded on the Balance Sheet. In some cases, the ''Historical Cost'' is used; such that the value of the asset when it was bought in the past is used as the monetary value. In other instances, the present fair market value of the asset is used to determine the value shown on the balance sheet. value of the assets owned by that firm. It covers money and other valuables belonging to an individual or to a business. ''Total assets'' can also be called the ''balance sheet total''. Assets can be grouped into two major classes: tangible assets and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
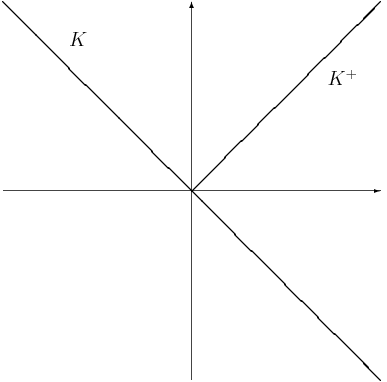
Solvency Cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs). Mathematical basis If given a bid-ask matrix \Pi for d assets such that \Pi = \left(\pi^\right)_ and m \leq d is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally m = d), then the solvency cone K(\Pi) \subset \mathbb^d is the convex cone spanned by the unit vectors e^i, 1 \leq i \leq m and the vectors \pi^e^i-e^j, 1 \leq i,j \leq d. Definition A solvency cone K is any closed convex cone such that K \subseteq \mathbb^d and K \supseteq \mathbb^d_+. Uses A process of (random) solvency cones \left\_^T is a model of a financial market. This is sometimes called a market process. The negative of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bid–ask Spread
The bid–ask spread (also bid–offer or bid/ask and buy/sell in the case of a market maker) is the difference between the prices quoted (either by a single market maker or in a Order book (trading), limit order book) for an immediate sale (Ask price, ask) and an immediate purchase (Bid price, bid) for Shares, stocks, futures contracts, Option (finance), options, or currency pairs in some auction scenario. The size of the bid–ask spread in a security is one measure of the liquidity of the market and of the size of the transaction cost. If the spread is 0 then it is a frictionless market, frictionless asset. Liquidity The trader initiating the transaction is said to demand market liquidity, liquidity, and the other party (counterparty) to the transaction supplies liquidity. Liquidity demanders place market orders and liquidity suppliers place limit orders. For a round trip (a purchase and sale together) the liquidity demander pays the spread and the liquidity supplier earns the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frictionless Market
In economic theory a frictionless market is a financial market without transaction costs. Friction is a type of market incompleteness. Every complete market is frictionless, but the converse does not hold. In a frictionless market the solvency cone is the halfspace normal to the unique price vector. The Black–Scholes model The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing Derivative (finance), derivative investment instruments. From the parabolic partial differential equation in the model, ... assumes a frictionless market. References Financial markets Mathematical finance {{finance-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arbitrage
Arbitrage (, ) is the practice of taking advantage of a difference in prices in two or more marketsstriking a combination of matching deals to capitalize on the difference, the profit being the difference between the market prices at which the unit is traded. Arbitrage has the effect of causing prices of the same or very similar assets in different markets to converge. When used by academics in economics, an arbitrage is a transaction that involves no negative cash flow at any probabilistic or temporal state and a positive cash flow in at least one state; in simple terms, it is the possibility of a risk-free profit after transaction costs. For example, an arbitrage opportunity is present when there is the possibility to instantaneously buy something for a low price and sell it for a higher price. In principle and in academic use, an arbitrage is risk-free; in common use, as in statistical arbitrage, it may refer to ''expected'' profit, though losses may occur, and in practic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product
In mathematics, the tensor product V \otimes W of two vector spaces V and W (over the same field) is a vector space to which is associated a bilinear map V\times W \rightarrow V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an element of V \otimes W denoted . An element of the form v \otimes w is called the tensor product of v and w. An element of V \otimes W is a tensor, and the tensor product of two vectors is sometimes called an ''elementary tensor'' or a ''decomposable tensor''. The elementary tensors span V \otimes W in the sense that every element of V \otimes W is a sum of elementary tensors. If bases are given for V and W, a basis of V \otimes W is formed by all tensor products of a basis element of V and a basis element of W. The tensor product of two vector spaces captures the properties of all bilinear maps in the sense that a bilinear map from V\times W into another vector space Z factors uniquely through a linear map V\otimes W\to Z (see the section below ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |