Von Klitzing constant

The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values
:$R_ = \frac = \frac ,$

where is the Hall voltage, is the channel current, is the elementary charge and is Planck's constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively.

The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation corresponds to one where the Fermi level is an energy with a finite density of states, though these states are localized (see Anderson localization).

The fractional quantum Hall effect is more complicated and still considered an open research problem. Its existence relies fundamentally on electron–electron interactions. In 1988, it was proposed that there was quantum Hall effect without Landau levels. This quantum Hall effect is referred to as the quantum anomalous Hall (QAH) effect. There is also a new concept of the quantum spin Hall effect which is an analogue of the quantum Hall effect, where spin currents flow instead of charge currents.

Applications

The quantization of the Hall conductance ($G_= 1/R_$) has the important property of being exceedingly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of to nearly one part in a billion. It has allowed for the definition of a new practical standard for electrical resistance, based on the resistance quantum given by the von Klitzing constant . This is named after Klaus von Klitzing, the discoverer of exact quantization. The quantum Hall effect also provides an extremely precise independent determination of the fine-structure constant, a quantity of fundamental importance in quantum electrodynamics.

In 1990, a fixed conventional value was defined for use in resistance calibrations worldwide. On 16 November 2018, the 26th meeting of the General Conference on Weights and Measures decided to fix exact values of (the Planck constant) and (the elementary charge), superseding the 1990 value with an exact permanent value .

Research Status

The integer quantum hall is considered part of ''exact quantization''. Exact quantization in full generality is not completely understood but it has been explained as a very subtle manifestation of the combination of the principle of gauge invariance together with another simmetry (see Anomalies). The integer quantum hall instead is considered a solved research problem and understood in the scope of TKNN formula and Chern-Simons Lagrangians.

The fractional quantum Hall effect is still considered an open research problem. The fractional quantum Hall effect can be also understood as an integer quantum Hall effect, although not of electrons but of charge-flux composites known as composite fermions. Other models to explain the Fractional Quantum Hall Effect also exists.
Currently it is considered an open research problem because no single, confirmed and agreed list of fractional quantum numbers exists, neither a single agreed model to explain all of them, although there are such claims in the scope of composite fermions and Non Abelian Chern-Simons Lagrangians.

History

The MOSFET (metal-oxide-semiconductor field-effect transistor), invented by Mohamed Atalla and Dawon Kahng at Bell Labs in 1959, enabled physicists to study electron behavior in a nearly ideal two-dimensional gas. In a MOSFET, conduction electrons travel in a thin surface layer, and a "gate" voltage controls the number of charge carriers in this layer. This allows researchers to explore quantum effects by operating high-purity MOSFETs at liquid helium temperatures.

The integer quantization of the Hall conductance was originally predicted by University of Tokyo researchers Tsuneya Ando, Yukio Matsumoto and Yasutada Uemura in 1975, on the basis of an approximate calculation which they themselves did not believe to be true. In 1978, the Gakushuin University researchers Jun-ichi Wakabayashi and Shinji Kawaji subsequently observed the effect in experiments carried out on the inversion layer of MOSFETs.

In 1980, Klaus von Klitzing, working at the high magnetic field laboratory in Grenoble with silicon-based MOSFET samples developed by Michael Pepper and Gerhard Dorda, made the unexpected discovery that the Hall resistance was ''exactly'' quantized. For this finding, von Klitzing was awarded the 1985 Nobel Prize in Physics. A link between exact quantization and gauge invariance was subsequently proposed by Robert Laughlin, who connected the quantized conductivity to the quantized charge transport in a Thouless charge pump. Most integer quantum Hall experiments are now performed on gallium arsenide heterostructures, although many other semiconductor materials can be used. In 2007, the integer quantum Hall effect was reported in graphene at temperatures as high as room temperature, and in the magnesium zinc oxide ZnO–Mg_''x''Zn_1−''x''O.

Integer quantum Hall effect

Landau levels

In two dimensions, when classical electrons are subjected to a magnetic field they follow circular cyclotron orbits. When the system is treated quantum mechanically, these orbits are quantized. To determine the values of the energy levels the Schrödinger equation must be solved.

Since the system is subjected to a magnetic field, it has to be introduced as an electromagnetic vector potential in the Schrödinger equation. The system considered is an electron gas that is free to move in the x and y directions, but is tightly confined in the z direction. Then, a magnetic field is applied in the z direction and according to the Landau gauge the electromagnetic vector potential is $\mathbf = (0, Bx, 0)$ and the scalar potential is $\phi=0$. Thus the Schrödinger equation for a particle of charge $q$ and effective mass $m^*$ in this system is:

:$\left \\psi(x,y,z)=\varepsilon\psi(x,y,z)$
where $\mathbf$ is the canonical momentum, which is replaced by the operator $-i\hbar\nabla$ and $\varepsilon$ is the total energy.

To solve this equation it is possible to separate it into two equations since the magnetic field just affects the movement along x and y axes. The total energy becomes then, the sum of two contributions $\varepsilon=\varepsilon_z+\varepsilon_$. The corresponding equations in z axis is:
:\left \frac + V(z) \right (z)=\varepsilon_zu(z)
To simplify things, the solution $V(z)$ is considered as an infinite well. Thus the solutions for the z direction are the energies $\varepsilon_z=\frac$, $n_z=1,2,3...$ and the wavefunctions are sinusoidal. For the $x$ and $y$ directions, the solution of the Schrödinger equation can be chosen to be the product of a plane wave in $y$-direction with some unknown function of $x$, i.e., $\psi_=u(x)e^$. This is because the vector potential does not depend on $y$ and the momentum operator $\hat p_y$ therefore commutes with the Hamiltonian. By substituting this Ansatz into the Schrödinger equation one gets the one-dimensional harmonic oscillator equation centered at $x_=\frac$.

:\left \frac +\fracm^*\omega_^2(x-l_B^2k_y)^2\right (x)=\varepsilon_u(x)
where $\omega_=\frac$ is defined as the cyclotron frequency and $l_B^2=\frac$ the magnetic length. The energies are:
:$\varepsilon_\equiv\varepsilon_=\hbar \omega_ \left ( n_x+\frac \right )$, $n_x=1,2,3...$

And the wavefunctions for the motion in the $xy$ plane are given by the product of a plane wave in $y$ and Hermite polynomials attenuated by the gaussian function in $x$, which are the wavefunctions of a harmonic oscillator.

From the expression for the Landau levels one notices that the energy depends only on $n_x$, not on $k_y$. States with the same $n_x$ but different $k_y$ are degenerate.

Density of states

At zero field, the density of states per unit surface for the two-dimensional electron gas taking into account degeneration due to spin is independent of the energy
:$n_=\frac$.
As the field is turned on, the density of states collapses from the constant to a Dirac comb, a series of Dirac $\delta$ functions, corresponding to the Landau levels separated $\Delta\varepsilon_=\hbar \omega_$. At finite temperature, however, the Landau levels acquire a width $\Gamma=\frac$ being $\tau_i$ the time between scattering events. Commonly it is assumed that the precise shape of Landau levels is a Gaussian or Lorentzian profile.

Another feature is that the wave functions form parallel strips in the $y$ -direction spaced equally along the $x$-axis, along the lines of $\mathbf$. Since there is nothing special about any direction in the $xy$-plane if the vector potential was differently chosen one should find circular symmetry.

Given a sample of dimensions $L_x \times L_y$ and applying the periodic boundary conditions in the $y$-direction $k=\fracj$ being $j$ an integer, one gets that each parabolic potential is placed at a value $x_k=l_B^2k$.

The number of states for each Landau Level and $k$ can be calculated from the ratio between the total magnetic flux that passes through the sample and the magnetic flux corresponding to a state.
:$N_B=\frac=\frac=\frac\begin& l_B&\\&=&\\ &&\end \frac\begin& \omega_&\\&=&\\ &&\end \frac$

Thus the density of states per unit surface is
:$n_B=\frac$.

Note the dependency of the density of states with the magnetic field. The larger the magnetic field is, the more states are in each Landau level. As a consequence, there is more confinement in the system since less energy levels are occupied.

Rewriting the last expression as $n_B=\frac \frac$ it is clear that each Landau level contains as many states as in a 2DEG in a $\Delta\varepsilon=\hbar \omega_$.

Given the fact that electrons are fermions, for each state available in the Landau levels it corresponds two electrons, one electron with each value for the spin $s=\pm\frac$. However, if a large magnetic field is applied, the energies split into two levels due to the magnetic moment associated with the alignment of the spin with the magnetic field. The difference in the energies is $\Delta E = \pm \fracg\mu_B$ being $g$ a factor which depends on the material ($g=2$ for free electrons) and $\mu_$ the Bohr magneton. The sign $+$ is taken when the spin is parallel to the field and $-$ when it is antiparallel. This fact called spin splitting implies that the density of states for each level is reduced by a half. Note that $\Delta E$ is proportional to the magnetic field so, the larger the magnetic field is, the more relevant is the split.

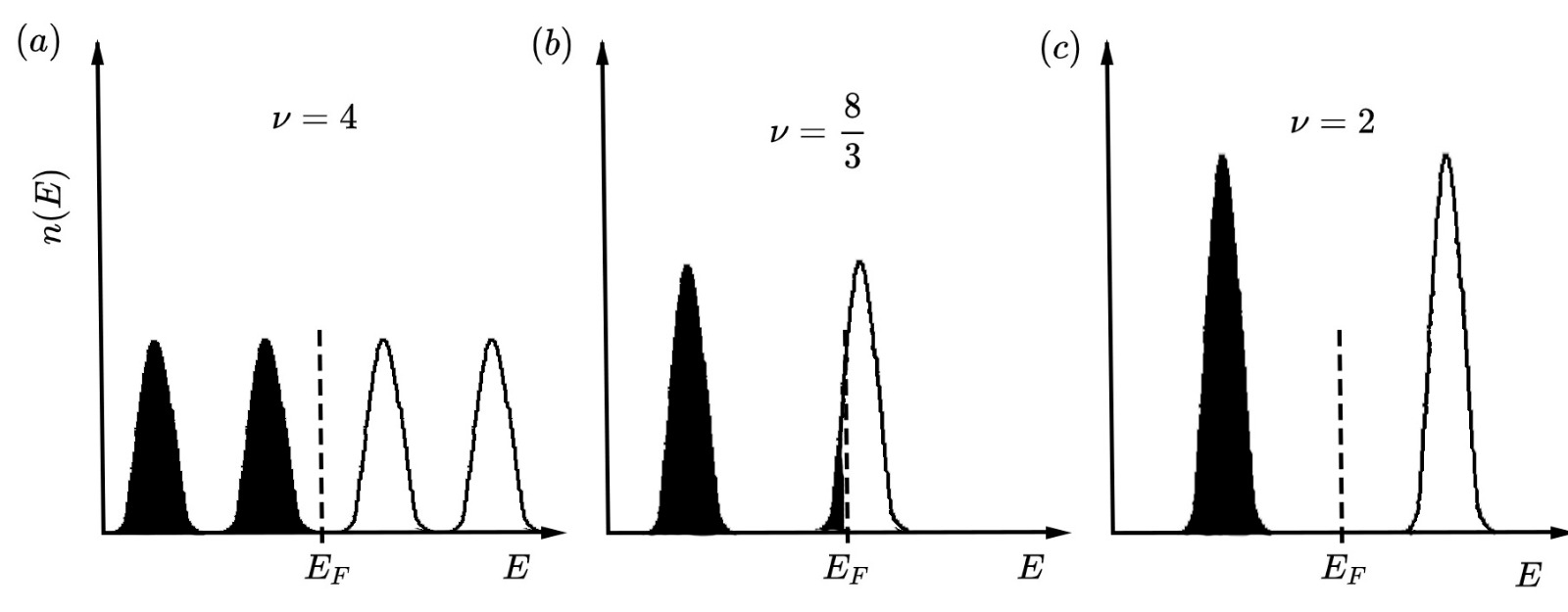
In order to get the number of occupied Landau levels, one defines the so-called filling factor $\nu$ as the ratio between the density of states in a 2DEG and the density of states in the Landau levels.

:$\nu=\frac=\frac$

In general the filling factor $\nu$ is not an integer. It happens to be an integer when there is an exact number of filled Landau levels. Instead, it becomes a non-integer when the top level is not fully occupied. Since $n_B\propto B$, by increasing the magnetic field, the Landau levels move up in energy and the number of states in each level grow, so fewer electrons occupy the top level until it becomes empty. If the magnetic field keeps increasing, eventually, all electrons will be in the lowest Landau level ($\nu<1$) and this is called the magnetic quantum limit.

Longitudinal resistivity

It is possible to relate the filling factor to the resistivity and hence, to the conductivity of the system. When $\nu$ is an integer, the Fermi energy lies in between Landau levels where there are no states available for carriers, so the conductivity becomes zero (it is considered that the magnetic field is big enough so that there is no overlap between Landau levels, otherwise there would be few electrons and the conductivity would be approximately $0$). Consequently, the resistivity becomes zero too (At very high magnetic fields it is proven that longitudinal conductivity and resistivity are proportional).

With the conductivity $\sigma=\rho^$ one finds

:$\sigma= \frac \begin \rho_&-\rho_\\ -\rho_&\rho_ \end \; .$

If the longitudinal resistivity is zero and transversal is finite, then $\det \rho \neq 0$. Thus both, the longitudinal conductivity and resistivity become zero.

Instead, when $\nu$ is a half-integer, the Fermi energy is located at the peak of the density distribution of some Landau Level. This means that the conductivity will have a maximum .

This distribution of minimums and maximums corresponds to ¨quantum oscillations¨ called ''Shubnikov–de Haas oscillations'' which become more relevant as the magnetic field increases. Obviously, the height of the peaks are larger as the magnetic field increases since the density of states increases with the field, so there are more carriers which contribute to the resistivity. It is interesting to notice that if the magnetic field is very small, the longitudinal resistivity is a constant which means that the classical result is reached.

Transverse resistivity

From the classical relation of the transverse resistivity $\rho_=\frac$ and substituting $n_=\nu \frac$ one finds out the quantization of the transverse resistivity and conductivity:

:$\rho_=\frac\Rightarrow \sigma=\nu \frac$

One concludes then, that the transverse resistivity is a multiple of the inverse of the so-called conductance quantum $e^2/h$. Nevertheless, in experiments a plateau is observed between Landau levels, which indicates that there are in fact charge carriers present. These carriers are localized in, for example, impurities of the material where they are trapped in orbits so they can not contribute to the conductivity. That is why the resistivity remains constant in between Landau levels. Again if the magnetic field decreases, one gets the classical result in which the resistivity is proportional to the magnetic field.

Photonic quantum Hall effect

The quantum Hall effect, in addition to being observed in two-dimensional electron systems, can be observed in photons. Photons do not possess inherent electric charge, but through the manipulation of discrete optical resonators and coupling phases or on-site phases, an artificial magnetic field can be created. This process can be expressed through a metaphor of photons bouncing between multiple mirrors. By shooting the light across multiple mirrors, the photons are routed and gain additional phase proportional to their angular momentum. This creates an effect like they are in a magnetic field.

Mathematics

The integers that appear in the Hall effect are examples of topological quantum numbers. They are known in mathematics as the first Chern numbers and are closely related to Berry's phase. A striking model of much interest in this context is the Azbel–Harper–Hofstadter model whose quantum phase diagram is the Hofstadter butterfly shown in the figure. The vertical axis is the strength of the magnetic field and the horizontal axis is the chemical potential, which fixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integers and cold colors negative integers. Note, however, that the density of states in these regions of quantized Hall conductance is zero; hence, they cannot produce the plateaus observed in the experiments. The phase diagram is fractal and has structure on all scales. In the figure there is an obvious self-similarity. In the presence of disorder, which is the source of the plateaus seen in the experiments, this diagram is very different and the fractal structure is mostly washed away.

Concerning physical mechanisms, impurities and/or particular states (e.g., edge currents) are important for both the 'integer' and 'fractional' effects. In addition, Coulomb interaction is also essential in the fractional quantum Hall effect. The observed strong similarity between integer and fractional quantum Hall effects is explained by the tendency of electrons to form bound states with an even number of magnetic flux quanta, called '' composite fermions''.

The Bohr atom interpretation of the von Klitzing constant

The value of the von Klitzing constant may be obtained already on the level of a single atom within the Bohr model while looking at it as a single-electron Hall effect. While during the cyclotron motion on a circular orbit the centrifugal force is balanced by the Lorentz force responsible for the transverse induced voltage and the Hall effect, one may look at the Coulomb potential difference in the Bohr atom as the induced single atom Hall voltage and the periodic electron motion on a circle as a Hall current. Defining the single atom Hall current as a rate a single electron charge $e$ is making Kepler revolutions with angular frequency $\omega$

:$I = \frac,$

and the induced Hall voltage as a difference between the hydrogen nucleus Coulomb potential at the electron orbital point and at infinity:

:$U=V_\text(\infty) - V_\text(r) = 0 - V_\text(r) = \frac$

One obtains the quantization of the defined Bohr orbit Hall resistance in steps of the von Klitzing constant as

:$R_\text(n) = \frac = n\frac$

which for the Bohr atom is linear but not inverse in the integer ''n''.

Relativistic analogs

Relativistic examples of the integer quantum Hall effect and quantum spin Hall effect arise in the context of lattice gauge theory.

See also

* Quantum Hall transitions
*Fractional quantum Hall effect
* Quantum anomalous Hall effect
* Quantum cellular automata
* Composite fermions
*Conductance Quantum
*Hall effect
*Hall probe
*Graphene
*Quantum spin Hall effect
* Coulomb potential between two current loops embedded in a magnetic field

References

Further reading

*
*
*''25 years of Quantum Hall Effect'', K. von Klitzing, Poincaré Seminar (Paris-2004)
PostscriptPdf

* Magnet Lab Press Releas

*
*Zyun F. Ezawa
''Quantum Hall Effects - Field Theoretical Approach and Related Topics.''
World Scientific, Singapore 2008,
*Sankar D. Sarma, Aron Pinczuk: ''Perspectives in Quantum Hall Effects.'' Wiley-VCH, Weinheim 2004,
*
* E. I. Rashba and V. B. Timofeev, Quantum Hall Effect, Sov. Phys. - Semiconductors v. 20, pp. 617–647 (1986).

{{Authority control

Hall effect
Condensed matter physics
Quantum electronics
Spintronics
Quantum phases
Mesoscopic physics
Articles containing video clips
1980 in science