Vibronic Transition on:
[Wikipedia]
[Google]
[Amazon]
Vibronic spectroscopy is a branch of molecular
 For absorption spectra, the vibrational coarse structure for a given electronic transition forms a single ''progression'', or series of transitions with a common level, here the lower level . There are no selection rules for vibrational quantum numbers, which are zero in the ground vibrational level of the initial electronic ground state, but can take any integer values in the final electronic excited state. The term values for a
For absorption spectra, the vibrational coarse structure for a given electronic transition forms a single ''progression'', or series of transitions with a common level, here the lower level . There are no selection rules for vibrational quantum numbers, which are zero in the ground vibrational level of the initial electronic ground state, but can take any integer values in the final electronic excited state. The term values for a  If emission occurs before vibrational relaxation can occur, then the resulting fluorescence is referred to as resonance fluorescence. In this case, the emission spectrum is identical to the absorbance spectrum. Resonance fluorescence, however, is not very common and is mainly observed in small molecules (such as diatomics) in the gas phase. This lack of prevalence is due to short radiative lifetimes of the excited state, during which energy can be lost.
Emission from the ground vibrational level of the excited state after vibrational relaxation is much more prevalent, referred to as relaxed fluorescence. Emission peaks for a molecule exhibiting relaxed fluorescence are found at longer wavelengths than the corresponding absorption spectra, with the difference being the Stokes shift of the molecule.
Vibronic spectra of diatomic molecules in the gas phase have been analyzed in detail. Vibrational coarse structure can sometimes be observed in the spectra of molecules in liquid or solid phases and of molecules in solution. Related phenomena including photoelectron spectroscopy,
If emission occurs before vibrational relaxation can occur, then the resulting fluorescence is referred to as resonance fluorescence. In this case, the emission spectrum is identical to the absorbance spectrum. Resonance fluorescence, however, is not very common and is mainly observed in small molecules (such as diatomics) in the gas phase. This lack of prevalence is due to short radiative lifetimes of the excited state, during which energy can be lost.
Emission from the ground vibrational level of the excited state after vibrational relaxation is much more prevalent, referred to as relaxed fluorescence. Emission peaks for a molecule exhibiting relaxed fluorescence are found at longer wavelengths than the corresponding absorption spectra, with the difference being the Stokes shift of the molecule.
Vibronic spectra of diatomic molecules in the gas phase have been analyzed in detail. Vibrational coarse structure can sometimes be observed in the spectra of molecules in liquid or solid phases and of molecules in solution. Related phenomena including photoelectron spectroscopy,
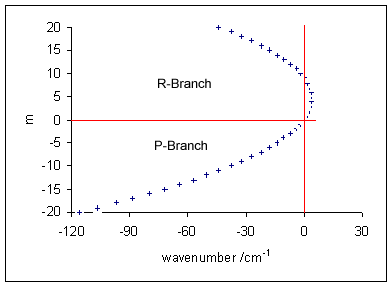 The treatment of rotational fine structure of vibronic transitions is similar to the treatment of rotation-vibration transitions and differs principally in the fact that the ground and excited states correspond to two different electronic states as well as to two different vibrational levels. For the P-branch , so that
Similarly for the R-branch , and
Thus, the wavenumbers of transitions in both P- and R-branches are given, to a first approximation, by the single formula
Here positive values refer to the R-branch (with ) and negative values refer to the P-branch (with ). The wavenumbers of the lines in the P-branch, on the low wavenumber side of the ''band origin'' at increase with . In the R-branch, for the usual case that , as increases the wavenumbers at first lie increasingly on the high wavenumber side of the band origin but then start to decrease, eventually lying on the low wavenumber side. The Fortrat diagram illustrates this effect.When centrifugal distortion is included the R-branch lines below the vibrational origin do not coincide with P-branch lines In the rigid rotor approximation the line wavenumbers lie on a
The treatment of rotational fine structure of vibronic transitions is similar to the treatment of rotation-vibration transitions and differs principally in the fact that the ground and excited states correspond to two different electronic states as well as to two different vibrational levels. For the P-branch , so that
Similarly for the R-branch , and
Thus, the wavenumbers of transitions in both P- and R-branches are given, to a first approximation, by the single formula
Here positive values refer to the R-branch (with ) and negative values refer to the P-branch (with ). The wavenumbers of the lines in the P-branch, on the low wavenumber side of the ''band origin'' at increase with . In the R-branch, for the usual case that , as increases the wavenumbers at first lie increasingly on the high wavenumber side of the band origin but then start to decrease, eventually lying on the low wavenumber side. The Fortrat diagram illustrates this effect.When centrifugal distortion is included the R-branch lines below the vibrational origin do not coincide with P-branch lines In the rigid rotor approximation the line wavenumbers lie on a
 As an example from
As an example from
spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum.
Spectro ...
concerned with vibronic transitions: the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
of the appropriate energy. In the gas phase
In the physical sciences, a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a ...
, vibronic transitions are also accompanied by changes in rotational
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersec ...
energy.
Vibronic spectra of diatomic molecule
Diatomic molecules () are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen () or oxygen (), then it is said to be homonuclear mol ...
s have been analysed in detail; emission spectra
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to electrons making a transition from a high energy state to a lower energy state. The photon energy of the ...
are more complicated than absorption spectra. The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. Vibronic spectroscopy may provide information, such as bond length
In molecular geometry, bond length or bond distance is defined as the average distance between Atomic nucleus, nuclei of two chemical bond, bonded atoms in a molecule. It is a Transferability (chemistry), transferable property of a bond between at ...
, on electronic excited states of stable molecules. It has also been applied to the study of unstable
In dynamical systems instability means that some of the outputs or internal state (controls), states increase with time, without bounds. Not all systems that are not Stability theory, stable are unstable; systems can also be marginal stability ...
molecules such as dicarbon (C2) in discharges, flames and astronomical objects
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists within the observable universe. In astronomy, the terms ''object'' and ''body'' are of ...
.Hollas, p. 211.
Principles
Electronic transitions are typically observed in the visible and ultraviolet regions, in the wavelength range approximately 200–700 nm (50,000–14,000 cm−1), whereas fundamental vibrations are observed below about 4000 cm−1.Energy is related to wavenumber by , where is thePlanck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
and is the velocity of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
When the electronic and vibrational energy changes are so different, vibronic coupling (mixing of electronic and vibrational wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s) can be neglected and the energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
of a vibronic level can be taken as the sum of the electronic and vibrational (and rotational) energies; that is, the Born–Oppenheimer approximation
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much h ...
applies. The overall molecular energy depends not only on the electronic state but also on vibrational and rotational quantum numbers, denoted v and J respectively for diatomic molecules. It is conventional to add a double prime for levels of the electronic ground state and a single prime for electronically excited states.
Each electronic transition may show vibrational coarse structure, and for molecules in the gas phase, rotational fine structure. This is true even when the molecule has a zero dipole moment and therefore has no vibration-rotation infrared spectrum or pure rotational microwave spectrum.
It is necessary to distinguish between absorption and emission spectra. With absorption the molecule starts in the ground electronic state, and usually also in the vibrational ground state because at ordinary temperatures the energy necessary for vibrational excitation is large compared to the average thermal energy. The molecule is excited to another electronic state and to many possible vibrational states . With emission, the molecule can start in various populated vibrational states, and finishes in the electronic ground state in one of many populated vibrational levels. The emission spectrum is more complicated than the absorption spectrum of the same molecule because there are more changes in vibrational energy level.
harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
are given by
where is a vibrational quantum number, and is the harmonic wavenumber. In the next approximation the term values are given by
where is an anharmonicity constant. This is, in effect, a better approximation to the Morse potential
The Morse potential, named after physicist Philip M. Morse, is a convenient
Interatomic potential, interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the oscillation, vibrational struct ...
near the potential minimum. The spacing between adjacent vibrational lines decreases with increasing quantum number because of anharmonicity in the vibration. Eventually the separation decreases to zero when the molecule photo-dissociates into a continuum of states. The second formula is adequate for small values of the vibrational quantum number. For higher values further anharmonicity terms are needed as the molecule approaches the dissociation limit, at the energy corresponding to the upper (final state) potential curve at infinite internuclear distance.
The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. The intensity distribution within a progression is governed by the difference in the equilibrium bond lengths of the initial electronic ground state and the final electronic excited state of the molecule. In accordance with the Born-Oppenheimer approximation, where electronic motion is near instantaneous compared to nuclear motion, transitions between vibrational levels happen with essentially no change in nuclear coordinates between the ground and excited electronic states. These nuclear coordinates are referred to as classical "turning points", where the equilibrium bond lengths of the initial and final electronic states are equal. These transitions can be represented as vertical lines between the various vibrational levels within electronic states on an energy level diagram.
It is generally true that the greater the changes to the bond length of a molecule upon excitation, the greater the contribution of vibrational states to a progression. The width of this progression itself is dependent on the range of transition energies available for internuclear distances close to the turning points of the initial vibration state. As the "well" of the potential energy curve of the final electronic state grows steeper, there are more final vibrational states available for transitions, and thus more energy levels to yield a wider spectrum.
Emission spectra are complicated due to the variety of processes through which electronically excited molecules can spontaneously return to lower energy states. There is a tendency for molecules to undergo vibrational energy relaxation, where energy is lost non-radiatively from the Franck–Condon state (the vibrational state achieved after a vertical transition) to surroundings or to internal processes. The molecules can settle in the ground vibrational level of the excited electronic state, where they can continue to decay to various vibrational levels in the ground electronic state, before ultimately returning to the lowest vibrational level of the ground state.
 If emission occurs before vibrational relaxation can occur, then the resulting fluorescence is referred to as resonance fluorescence. In this case, the emission spectrum is identical to the absorbance spectrum. Resonance fluorescence, however, is not very common and is mainly observed in small molecules (such as diatomics) in the gas phase. This lack of prevalence is due to short radiative lifetimes of the excited state, during which energy can be lost.
Emission from the ground vibrational level of the excited state after vibrational relaxation is much more prevalent, referred to as relaxed fluorescence. Emission peaks for a molecule exhibiting relaxed fluorescence are found at longer wavelengths than the corresponding absorption spectra, with the difference being the Stokes shift of the molecule.
Vibronic spectra of diatomic molecules in the gas phase have been analyzed in detail. Vibrational coarse structure can sometimes be observed in the spectra of molecules in liquid or solid phases and of molecules in solution. Related phenomena including photoelectron spectroscopy,
If emission occurs before vibrational relaxation can occur, then the resulting fluorescence is referred to as resonance fluorescence. In this case, the emission spectrum is identical to the absorbance spectrum. Resonance fluorescence, however, is not very common and is mainly observed in small molecules (such as diatomics) in the gas phase. This lack of prevalence is due to short radiative lifetimes of the excited state, during which energy can be lost.
Emission from the ground vibrational level of the excited state after vibrational relaxation is much more prevalent, referred to as relaxed fluorescence. Emission peaks for a molecule exhibiting relaxed fluorescence are found at longer wavelengths than the corresponding absorption spectra, with the difference being the Stokes shift of the molecule.
Vibronic spectra of diatomic molecules in the gas phase have been analyzed in detail. Vibrational coarse structure can sometimes be observed in the spectra of molecules in liquid or solid phases and of molecules in solution. Related phenomena including photoelectron spectroscopy, resonance Raman spectroscopy
Resonance Raman spectroscopy (RR spectroscopy or RRS) is a variant of Raman spectroscopy in which the incident photon energy is close in energy to an electronic transition of a compound or material under examination. This similarity in energy (re ...
, luminescence
Luminescence is a spontaneous emission of radiation from an electronically or vibrationally excited species not in thermal equilibrium with its environment. A luminescent object emits ''cold light'' in contrast to incandescence, where an obje ...
, and fluorescence
Fluorescence is one of two kinds of photoluminescence, the emission of light by a substance that has absorbed light or other electromagnetic radiation. When exposed to ultraviolet radiation, many substances will glow (fluoresce) with colore ...
are not discussed in this article, though they also involve vibronic transitions.
Diatomic molecules
The vibronic spectra of diatomic molecules in the gas phase also show rotational fine structure. Each line in a vibrational progression will show P- and R-branches. For some electronic transitions there will also be a Q-branch. The transition energies, expressed in wavenumbers, of the lines for a particular vibronic transition are given, in therigid rotor
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special r ...
approximation, that is, ignoring centrifugal distortion, byBanwell and McCash, p. 171
Here are rotational constant
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special r ...
s and are rotational quantum number
In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system.
To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantu ...
s. (For B also, a double prime indicates the ground state and a single prime an electronically excited state.) The values of the rotational constants may differ appreciably because the bond length in the electronic excited state may be quite different from the bond length in the ground state, because of the operation of the Franck-Condon principle. The rotational constant is inversely proportional to the square of the bond length. Usually as is true when an electron is promoted from a bonding orbital to an antibonding orbital, causing bond lengthening. But this is not always the case; if an electron is promoted from a non-bonding or antibonding orbital to a bonding orbital, there will be bond-shortening and .
 The treatment of rotational fine structure of vibronic transitions is similar to the treatment of rotation-vibration transitions and differs principally in the fact that the ground and excited states correspond to two different electronic states as well as to two different vibrational levels. For the P-branch , so that
Similarly for the R-branch , and
Thus, the wavenumbers of transitions in both P- and R-branches are given, to a first approximation, by the single formula
Here positive values refer to the R-branch (with ) and negative values refer to the P-branch (with ). The wavenumbers of the lines in the P-branch, on the low wavenumber side of the ''band origin'' at increase with . In the R-branch, for the usual case that , as increases the wavenumbers at first lie increasingly on the high wavenumber side of the band origin but then start to decrease, eventually lying on the low wavenumber side. The Fortrat diagram illustrates this effect.When centrifugal distortion is included the R-branch lines below the vibrational origin do not coincide with P-branch lines In the rigid rotor approximation the line wavenumbers lie on a
The treatment of rotational fine structure of vibronic transitions is similar to the treatment of rotation-vibration transitions and differs principally in the fact that the ground and excited states correspond to two different electronic states as well as to two different vibrational levels. For the P-branch , so that
Similarly for the R-branch , and
Thus, the wavenumbers of transitions in both P- and R-branches are given, to a first approximation, by the single formula
Here positive values refer to the R-branch (with ) and negative values refer to the P-branch (with ). The wavenumbers of the lines in the P-branch, on the low wavenumber side of the ''band origin'' at increase with . In the R-branch, for the usual case that , as increases the wavenumbers at first lie increasingly on the high wavenumber side of the band origin but then start to decrease, eventually lying on the low wavenumber side. The Fortrat diagram illustrates this effect.When centrifugal distortion is included the R-branch lines below the vibrational origin do not coincide with P-branch lines In the rigid rotor approximation the line wavenumbers lie on a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
which has a maximum at
The line of highest wavenumber in the R-branch is known as the ''band head''. It occurs at the value of which is equal to the integer part
In mathematics, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or eq ...
of , or of .
When a Q-branch is allowed for a particular electronic transition, the lines of the Q-branch correspond to the case , and wavenumbers are given by
The Q-branch then consists of a series of lines with increasing separation between adjacent lines as increases. When the Q-branch lies to lower wavenumbers relative to the vibrational line.
Predissociation
The phenomenon of predissociation occurs when an electronic transition results in dissociation of the molecule at an excitation energy less than the normal dissociation limit of the upper state. This can occur when the potential energy curve of the upper state crosses the curve for a repulsive state, so that the two states have equal energy at some internuclear distance. This allows the possibility of a radiationless transition to the repulsive state whose energy levels form a continuum, so that there is blurring of the particular vibrational band in the vibrational progression.Applications
The analysis of vibronic spectra of diatomic molecules provides information concerning both the ground electronic state and the excited electronic state. Data for the ground state can also be obtained by vibrational or pure rotational spectroscopy, but data for the excited state can only be obtained from the analysis of vibronic spectra. For example, the bond length in the excited state may be derived from the value of the rotational constant ''B''′. In addition to stable diatomic molecules, vibronic spectroscopy has been used to study unstable species, including CH, NH,hydroxyl radical
The hydroxyl radical, •HO, is the neutral form of the hydroxide ion (HO–). Hydroxyl radicals are highly reactive and consequently short-lived; however, they form an important part of radical chemistry. Most notably hydroxyl radicals are pr ...
, OH, and cyano radical, CN. The Swan bands in hydrocarbon flame spectra are a progression in the C–C stretching vibration of the dicarbon radical, C2 for the electronic transition. Vibronic bands for 9 other electronic transitions of C2 have been observed in the infrared and ultraviolet regions.
Polyatomic molecules and ions
For polyatomic molecules, progressions are most often observed when the change in bond lengths upon electronic excitation coincides with the change due to a ″totally symmetric″ vibration.In a ″totally symmetric″ vibration the lengths of all symmetrically-equivalent bonds vary in phase with each other. The symmetry of the molecule is the same in the vibrational excited state as in the vibrational ground state. This is the same process that occurs inresonance Raman spectroscopy
Resonance Raman spectroscopy (RR spectroscopy or RRS) is a variant of Raman spectroscopy in which the incident photon energy is close in energy to an electronic transition of a compound or material under examination. This similarity in energy (re ...
. For example, in formaldehyde
Formaldehyde ( , ) (systematic name methanal) is an organic compound with the chemical formula and structure , more precisely . The compound is a pungent, colourless gas that polymerises spontaneously into paraformaldehyde. It is stored as ...
(methanal), H2CO, the transition involves excitation of an electron from a non-bonding orbital to an antibonding pi orbital which weakens and lengthens the C–O bond. This produces a long progression in the C–O stretching vibration. Another example is furnished by benzene
Benzene is an Organic compound, organic chemical compound with the Chemical formula#Molecular formula, molecular formula C6H6. The benzene molecule is composed of six carbon atoms joined in a planar hexagonal Ring (chemistry), ring with one hyd ...
, C6H6. In both gas and liquid phase the band around 250 nm shows a progression in the symmetric ring-breathing vibration.
 As an example from
As an example from inorganic chemistry
Inorganic chemistry deals with chemical synthesis, synthesis and behavior of inorganic compound, inorganic and organometallic chemistry, organometallic compounds. This field covers chemical compounds that are not carbon-based, which are the subj ...
the permanganate
A permanganate () is a chemical compound with the manganate(VII) ion, , the conjugate base of permanganic acid. Because the manganese atom has a +7 oxidation state, the permanganate(VII) ion is a strong oxidising agent. The ion is a transition ...
ion, , in aqueous solution has an intense purple colour due to an ligand-to-metal charge transfer band (LMCT) in much of the visible region. This band shows a progression in the symmetric Mn–O stretching vibration. The individual lines overlap each other extensively, giving rise to a broad overall profile with some coarse structure.
Progressions in vibrations which are not totally symmetric may also be observed.
''d''–''d'' electronic transitions in atoms in a centrosymmetric
In crystallography, a centrosymmetric point group contains an inversion center as one of its symmetry elements. In such a point group, for every point (x, y, z) in the unit cell there is an indistinguishable point (-x, -y, -z). Such point grou ...
environment are electric-dipole forbidden by the Laporte rule
The Laporte rule is a rule that explains the intensities of absorption spectra for chemical species. It is a selection rule that rigorously applies to atoms, and to molecules that are centrosymmetric, i.e. with an inversion centre. It states that ...
. This will apply to octahedral
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
coordination compound
A coordination complex is a chemical compound consisting of a central atom or ion, which is usually metallic and is called the ''coordination centre'', and a surrounding array of chemical bond, bound molecules or ions, that are in turn known as ' ...
s of the transition metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. The lanthanide and actinid ...
s. The spectra of many of these complexes have some vibronic character. The same rule also applies to ''f''–''f'' transitions in centrosymmetric complexes of lanthanide
The lanthanide () or lanthanoid () series of chemical elements comprises at least the 14 metallic chemical elements with atomic numbers 57–70, from lanthanum through ytterbium. In the periodic table, they fill the 4f orbitals. Lutetium (el ...
s and actinide
The actinide () or actinoid () series encompasses at least the 14 metallic chemical elements in the 5f series, with atomic numbers from 89 to 102, actinium through nobelium. Number 103, lawrencium, is also generally included despite being part ...
s. In the case of the octahedral actinide chloro-complex of uranium
Uranium is a chemical element; it has chemical symbol, symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Ura ...
(IV), UCl62− the observed electronic spectrum is entirely vibronic. At the temperature of liquid helium, 4 K, the vibronic structure was completely resolved, with zero intensity for the purely electronic transition, and three side-lines corresponding to the asymmetric U–Cl stretching vibration and two asymmetric Cl–U–Cl bending modes. Later studies on the same anion were also able to account for vibronic transitions involving low-frequency lattice vibration
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined ...
s.
Notes
References
Bibliography
* Chapter: Molecular Spectroscopy 2. * * * * * * * Chapter 4: Fundamentals of Fluorescence and Fluorescence Microscopy {{Branches of spectroscopy Spectroscopy