Variance-based Sensitivity Analysis

Variance-based sensitivity analysis (often referred to as the Sobol’ method or Sobol’ indices, after Ilya M. Sobol’) is a form of global sensitivity analysis.Sobol, I.M. (2001), Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. ''MATH COMPUT SIMULAT'',55(1–3),271-280, Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D. Saisana, M., and Tarantola, S., 2008, ''Global Sensitivity Analysis. The Primer'', John Wiley & Sons. Working within a probabilistic framework, it decomposes the variance of the output of the model or system into fractions which can be attributed to inputs or sets of inputs. For example, given a model with two inputs and one output, one might find that 70% of the output variance is caused by the variance in the first input, 20% by the variance in the second, and 10% due to interactions between the two. These percentages are directly interpreted as measures of sensitivity. Variance-based measures of sensitivity are attractive because they measure sensitivity across the whole input space (i.e. it is a global method), they can deal with nonlinear responses, and they can measure the effect of interactions in non-additive systems.Saltelli, A., Annoni, P., 2010, How to avoid a perfunctory sensitivity analysis, ''Environmental Modeling and Software'' 25, 1508–1517.

Decomposition of variance

From a black box perspective, any model may be viewed as a function ''Y''=''f''(X), where X is a vector of ''d'' uncertain model inputs , and ''Y'' is a chosen univariate model output (note that this approach examines scalar model outputs, but multiple outputs can be analysed by multiple independent sensitivity analyses). Furthermore, it will be assumed that the inputs are independently and uniformly distributed within the unit hypercube, i.e. X_i \in ,1 for $i=1,2,...,d$. This incurs no loss of generality because any input space can be transformed onto this unit hypercube. ''f''(X) may be decomposed in the following way,Sobol’, I. (1990). Sensitivity estimates for nonlinear mathematical models. ''Matematicheskoe Modelirovanie'' 2, 112–118. in Russian, translated in English in Sobol’ , I. (1993). Sensitivity analysis for non-linear mathematical models. ''Mathematical Modeling & Computational Experiment (Engl. Transl.)'', 1993, 1, 407–414.

:$Y = f_0 + \sum_^d f_i(X_i) + \sum_^ f_(X_i,X_j) + \cdots + f_(X_1,X_2,\dots,X_d)$

where ''f''₀ is a constant and ''f''_''i'' is a function of ''X''_''i'', ''f''_''ij'' a function of ''X''_''i'' and ''X''_''j'', etc. A condition of this decomposition is that,

:$\int_0^1 f_(X_,X_,\dots,X_) dX_=0, \text k = i_1,...,i_s$

i.e. all the terms in the functional decomposition are orthogonal. This leads to definitions of the terms of the functional decomposition in terms of conditional expected values,

:$f_0 = E(Y)$

:$f_i(X_i) = E(Y, X_i) - f_0$

:$f_(X_i,X_j) = E(Y, X_i,X_j) - f_0 - f_i - f_j$

From which it can be seen that ''f''_''i'' is the effect of varying ''X''_''i'' alone (known as the main effect of ''X''_''i''), and ''f''_''ij'' is the effect of varying ''X''_''i'' and ''X''_''j'' simultaneously, ''additional to the effect of their individual variations''. This is known as a second-order interaction. Higher-order terms have analogous definitions.

Now, further assuming that the ''f''(X) is square-integrable, the functional decomposition may be squared and integrated to give,

:$\int f^2(\mathbf) d\mathbf - f_0^2 = \sum_^d \sum_^d \int f_^2 dX_ \dots dX_$

Notice that the left hand side is equal to the variance of ''Y'', and the terms of the right hand side are variance terms, now decomposed with respect to sets of the ''X''_''i''. This finally leads to the decomposition of variance expression,

:$\operatorname(Y) = \sum_^d V_i + \sum_^ V_ + \cdots + V_$

where

:$V_ = \operatorname_ \left( E_ (Y \mid X_) \right)$,

:$V_ = \operatorname_ \left( E_ \left( Y \mid X_i, X_j\right)\right) - V_ - V_$

and so on. The ''X''_~''i'' notation indicates the set of all variables ''except'' ''X''_''i''. The above variance decomposition shows how the variance of the model output can be decomposed into terms attributable to each input, as well as the interaction effects between them. Together, all terms sum to the total variance of the model output.

First-order indices

A direct variance-based measure of sensitivity ''S''_''i'', called the "first-order sensitivity index", or "main effect index" is stated as follows,

:$S_i = \frac$

This is the contribution to the output variance of the main effect of ''X''_''i'', therefore it measures the effect of varying ''X''_''i'' ''alone'', but averaged over variations in other input parameters. It is standardised by the total variance to provide a fractional contribution. Higher-order interaction indices ''S''_''ij'', ''S''_''ijk'' and so on can be formed by dividing other terms in the variance decomposition by Var(''Y''). Note that this has the implication that,

:$\sum_^d S_i + \sum_^ S_ + \cdots + S_ = 1$

Total-effect index

Using the ''S''_''i'', ''S''_''ij'' and higher-order indices given above, one can build a picture of the importance of each variable in determining the output variance. However, when the number of variables is large, this requires the evaluation of 2^''d''-1 indices, which can be too computationally demanding. For this reason, a measure known as the "Total-effect index" or "Total-order index", ''S''_''Ti'', is used. This measures the contribution to the output variance of ''X''_''i'', ''including'' all variance caused by its interactions, of any order, with any other input variables. It is given as,

:$S_ = \frac = 1 - \frac$

Note that unlike the ''S''_''i'',

:$\sum_^d S_ \geq 1$

due to the fact that the interaction effect between e.g. ''X''_''i'' and ''X''_''j'' is counted in both ''S''_''Ti'' ''and'' ''S''_''Tj''. In fact, the sum of the ''S''_''Ti'' will only be equal to 1 when the model is purely additive.

Calculation of indices

For analytically tractable functions, the indices above may be calculated analytically by evaluating the integrals in the decomposition. However, in the vast majority of cases they are estimated – this is usually done by the Monte Carlo method.

Sampling sequences

The Monte Carlo approach involves generating a sequence of randomly distributed points inside the unit hypercube (strictly speaking these will be pseudorandom). In practice, it is common to substitute random sequences with low-discrepancy sequences to improve the efficiency of the estimators. This is then known as the quasi-Monte Carlo method. Some low-discrepancy sequences commonly used in sensitivity analysis include the Sobol’ sequence and the Latin hypercube design.

Procedure

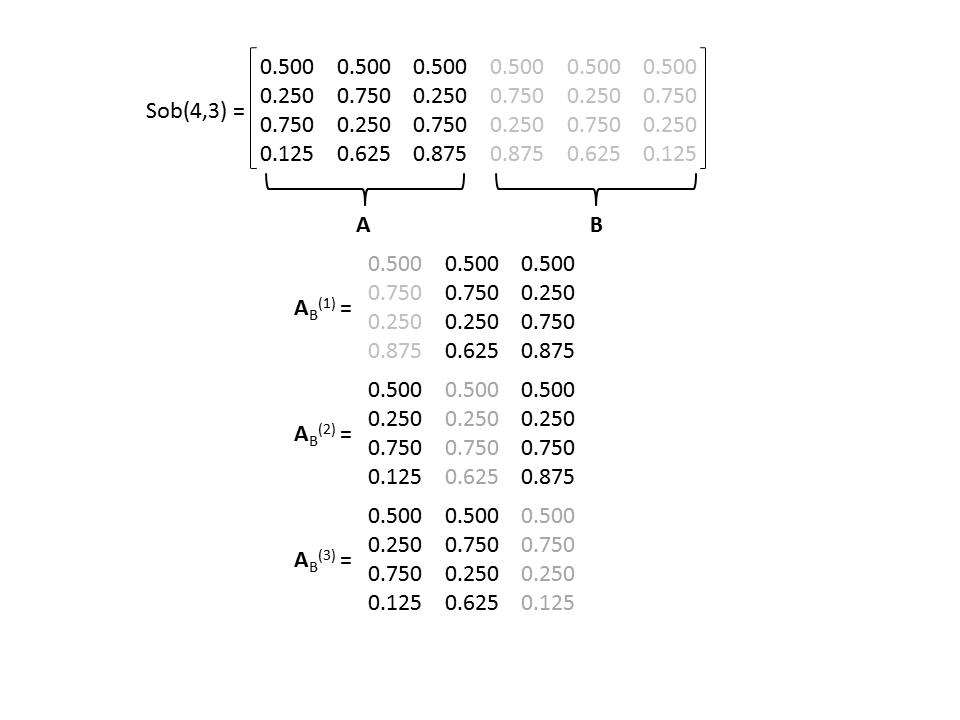
To calculate the indices using the (quasi) Monte Carlo method, the following steps are used:

# Generate an ''N''×2''d'' sample matrix, i.e. each row is a sample point in the hyperspace of 2''d'' dimensions. This should be done with respect to the probability distributions of the input variables.
# Use the first ''d'' columns of the matrix as matrix A, and the remaining ''d'' columns as matrix B. This effectively gives two independent samples of ''N'' points in the ''d''-dimensional unit hypercube.
# Build ''d'' further ''N''×''d'' matrices A_B^''i'', for ''i'' = 1,2,...,d, such that the ''i''th column of A_B^''i'' is equal to the ''i''th column of B, and the remaining columns are from A.
# The A, B, and the ''d'' A_B^''i'' matrices in total specify ''N''(''d''+2) points in the input space (one for each row). Run the model at each design point in the A, B, and A_B^''i'' matrices, giving a total of ''N''(''d''+2) model evaluations – the corresponding f(A), f(B) and f(A_B^''i'') values.
# Calculate the sensitivity indices using the estimators below.

The accuracy of the estimators is of course dependent on ''N''. The value of ''N'' can be chosen by sequentially adding points and calculating the indices until the estimated values reach some acceptable convergence. For this reason, when using low-discrepancy sequences, it can be advantageous to use those that allow sequential addition of points (such as the Sobol’ sequence), as compared to those that do not (such as Latin hypercube sequences).

Estimators

There are a number of possible Monte Carlo estimators available for both indices. Two that are currently in general use are,Andrea Saltelli, Paola Annoni, Ivano Azzini, Francesca Campolongo, Marco Ratto, and Stefano Tarantola. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. ''Computer Physics Communications'', 181(2):259{270, 2010

: $\operatorname{Var}_{X_i}(E_{\mathbf{X}_{\sim i(Y, X_i)) \approx { \frac {1}{N} \sum_{j=1}^{N} f \left ( \mathbf{B} \right )_{j} \left ( f \left ( \mathbf{A}^i_B \right )_{j} - f \left ( \mathbf{A} \right )_{j} \right ) }$

and

: $E_{\mathbf{X}_{\sim i\left(\operatorname{Var}_{X_i}\left(Y \mid \mathbf{X}_{\sim i} \right) \right) \approx {\frac {1}{2N}\sum_{j=1}^{N} \left( f \left ( \mathbf{A} \right )_{j} - f \left (\mathbf{A}^i_B \right )_{j}\right )^2 }$

for the estimation of the ''S''_''i'' and the ''S''_''Ti'' respectively.

Computational expense

For the estimation of the ''S''_''i'' and the ''S''_''Ti'' for all input variables, ''N''(''d''+2) model runs are required. Since ''N'' is often of the order of hundreds or thousands of runs, computational expense can quickly become a problem when the model takes a significant amount of time for a single run. In such cases, there are a number of techniques available to reduce the computational cost of estimating sensitivity indices, such as emulators, HDMR and FAST.

See also

* Sensitivity analysis
* Monte Carlo method
* Quasi-Monte Carlo method
* Sobol’ sequence

References

{{Reflist

Mathematical modeling

fr:Indice de Sobol