Two-body problem in general relativity on:
[Wikipedia]
[Google]
[Amazon]
The two-body problem in general relativity (or relativistic two-body problem) is the determination of the motion and
 The Kepler problem derives its name from
The Kepler problem derives its name from
 If the potential energy between the two bodies is not exactly the 1/''r'' potential of Newton's gravitational law but differs only slightly, then the ellipse of the orbit gradually rotates (among other possible effects). This
If the potential energy between the two bodies is not exactly the 1/''r'' potential of Newton's gravitational law but differs only slightly, then the ellipse of the orbit gradually rotates (among other possible effects). This
 In 1859,
In 1859,
 Around 1904–1905, the works of
Around 1904–1905, the works of
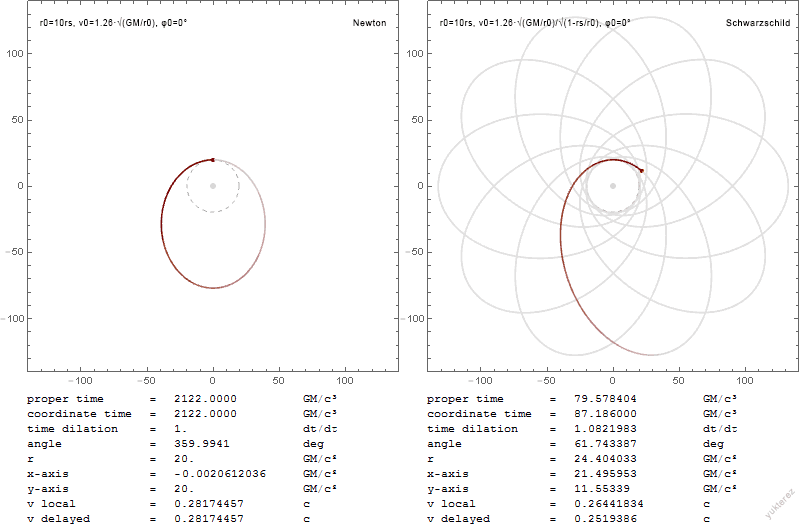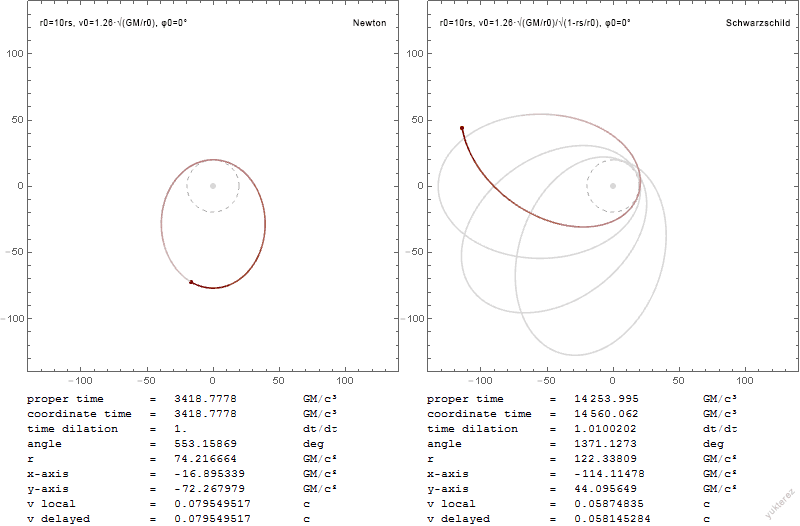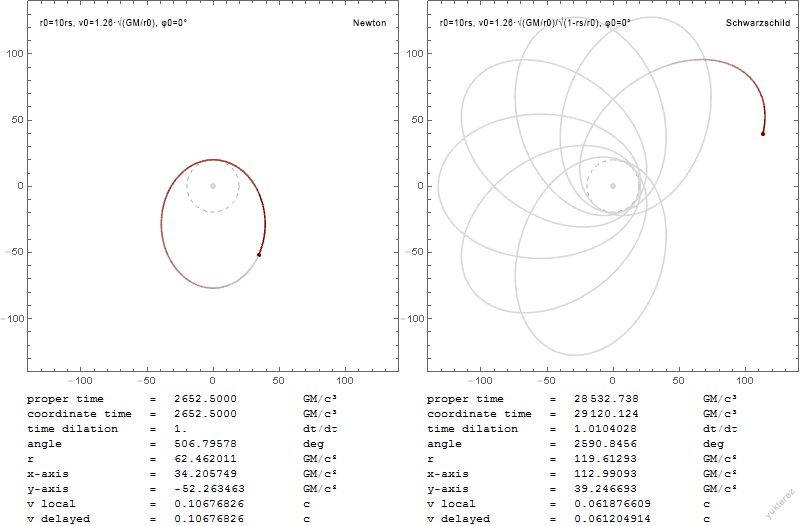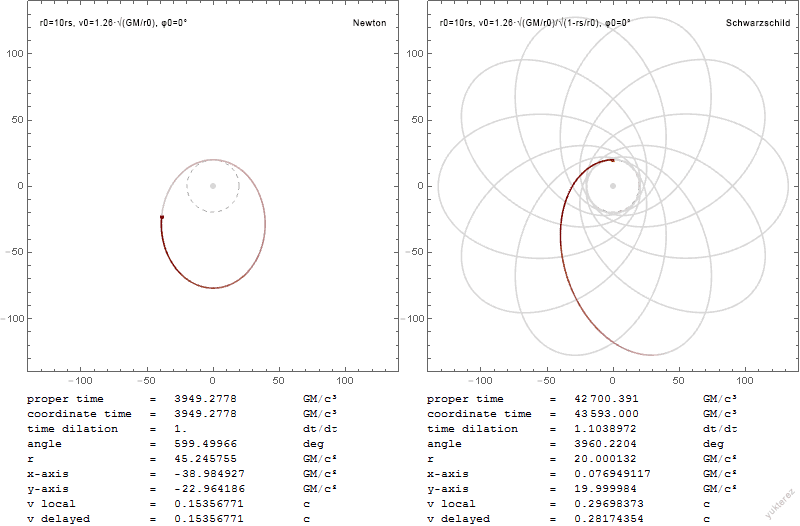 The orbits of a test particle of infinitesimal mass about the central mass is given by the equation of motion
where is the
The orbits of a test particle of infinitesimal mass about the central mass is given by the equation of motion
where is the
 The effective potential ''V'' can be re-written in terms of the length :
Circular orbits are possible when the effective force is zero:
i.e., when the two attractive forces—Newtonian gravity (first term) and the attraction unique to general relativity (third term)—are exactly balanced by the repulsive centrifugal force (second term). There are two radii at which this balancing can occur, denoted here as ''r''inner and ''r''outer:
which are obtained using the
The effective potential ''V'' can be re-written in terms of the length :
Circular orbits are possible when the effective force is zero:
i.e., when the two attractive forces—Newtonian gravity (first term) and the attraction unique to general relativity (third term)—are exactly balanced by the repulsive centrifugal force (second term). There are two radii at which this balancing can occur, denoted here as ''r''inner and ''r''outer:
which are obtained using the  Substituting the definitions of ''a'' and ''r''s into ''r''outer yields the classical formula for a particle of mass ''m'' orbiting a body of mass ''M''.
The following equation
where ''ω''''φ'' is the orbital angular speed of the particle, is obtained in non-relativistic mechanics by setting the
Substituting the definitions of ''a'' and ''r''s into ''r''outer yields the classical formula for a particle of mass ''m'' orbiting a body of mass ''M''.
The following equation
where ''ω''''φ'' is the orbital angular speed of the particle, is obtained in non-relativistic mechanics by setting the
 The orbital precession rate may be derived using this radial effective potential ''V''. A small radial deviation from a circular orbit of radius ''r''outer will oscillate in a stable manner with an angular frequency
which equals
Taking the square root of both sides and expanding using the
The orbital precession rate may be derived using this radial effective potential ''V''. A small radial deviation from a circular orbit of radius ''r''outer will oscillate in a stable manner with an angular frequency
which equals
Taking the square root of both sides and expanding using the

File:PSR B1913+16 periastron shift graph.svg, Experimentally observed changes in the time of the
Animation
showing relativistic precession of stars around the Milky Way supermassive black hole
from ''Reflections on Relativity'' by Kevin Brown. {{Relativity Exact solutions in general relativity
gravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
of two bodies as described by the field equations of general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
. Solving the Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attra ...
is essential to calculate the bending of light by gravity and the motion of a planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
orbiting its sun. Solutions are also used to describe the motion of binary star
A binary star or binary star system is a system of two stars that are gravitationally bound to and in orbit around each other. Binary stars in the night sky that are seen as a single object to the naked eye are often resolved as separate stars us ...
s around each other, and estimate their gradual loss of energy through gravitational radiation
Gravitational waves are oscillations of the gravitational field that travel through space at the speed of light; they are generated by the relative motion of gravitating masses. They were proposed by Oliver Heaviside in 1893 and then later by ...
.
General relativity describes the gravitational field by curved space-time; the field equations governing this curvature are nonlinear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
and therefore difficult to solve in a closed form. No exact solutions of the Kepler problem have been found, but an approximate solution has: the Schwarzschild solution. This solution pertains when the mass ''M'' of one body is overwhelmingly greater than the mass ''m'' of the other. If so, the larger mass may be taken as stationary and the sole contributor to the gravitational field. This is a good approximation for a photon passing a star and for a planet orbiting its sun. The motion of the lighter body (called the "particle" below) can then be determined from the Schwarzschild solution; the motion is a geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
("shortest path between two points") in the curved space-time. Such geodesic solutions account for the anomalous precession of the planet Mercury, which is a key piece of evidence supporting the theory of general relativity. They also describe the bending of light in a gravitational field, another prediction famously used as evidence for general relativity.
If both masses are considered to contribute to the gravitational field, as in binary stars, the Kepler problem can be solved only approximately. The earliest approximation method to be developed was the post-Newtonian expansion
In general relativity, post-Newtonian expansions (PN expansions) are used for finding an approximate solution of Einstein field equations for the metric tensor (general relativity), metric tensor. The approximations are expanded in small paramet ...
, an iterative method in which an initial solution is gradually corrected. More recently, it has become possible to solve Einstein's field equation using a computer instead of mathematical formulae. As the two bodies orbit each other, they will emit gravitational radiation
Gravitational waves are oscillations of the gravitational field that travel through space at the speed of light; they are generated by the relative motion of gravitating masses. They were proposed by Oliver Heaviside in 1893 and then later by ...
; this causes them to lose energy and angular momentum gradually, as illustrated by the binary pulsar PSR B1913+16.
For binary black hole
A binary black hole (BBH), or black hole binary, is an astronomical object consisting of two black holes in close orbit around each other. Like black holes themselves, binary black holes are often divided into binary stellar black holes, formed e ...
s, the numerical solution of the two-body problem was achieved in 2005 after four decades of research when three groups devised breakthrough techniques.
Historical context
Classical Kepler problem
 The Kepler problem derives its name from
The Kepler problem derives its name from Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
, who worked as an assistant to the Danish astronomer Tycho Brahe
Tycho Brahe ( ; ; born Tyge Ottesen Brahe, ; 14 December 154624 October 1601), generally called Tycho for short, was a Danish astronomer of the Renaissance, known for his comprehensive and unprecedentedly accurate astronomical observations. He ...
. Brahe took extraordinarily accurate measurements of the motion of the planets of the Solar System. From these measurements, Kepler was able to formulate Kepler's laws
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in ...
, the first modern description of planetary motion:
# The orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an ...
of every planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
is an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
with the Sun at one of the two foci.
# A line joining a planet and the Sun sweeps out equal area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
s during equal intervals of time.
# The square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
of the orbital period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets ...
of a planet is directly proportional to the cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
of the semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
of its orbit.
Kepler published the first two laws in 1609 and the third law in 1619. They supplanted earlier models of the Solar System, such as those of Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
and Copernicus
Nicolaus Copernicus (19 February 1473 – 24 May 1543) was a Renaissance polymath who formulated a mathematical model, model of Celestial spheres#Renaissance, the universe that placed heliocentrism, the Sun rather than Earth at its cen ...
. Kepler's laws apply only in the limited case of the two-body problem. Voltaire
François-Marie Arouet (; 21 November 169430 May 1778), known by his ''Pen name, nom de plume'' Voltaire (, ; ), was a French Age of Enlightenment, Enlightenment writer, philosopher (''philosophe''), satirist, and historian. Famous for his wit ...
and Émilie du Châtelet
Gabrielle Émilie Le Tonnelier de Breteuil, Marquise du Châtelet (; 17 December 1706 – 10 September 1749) was a French mathematician and physicist.
Her most recognized achievement is her philosophical magnum opus, ''Institutions de Physique'' ...
were the first to call them "Kepler's laws".
Nearly a century later, Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
had formulated his three laws of motion. In particular, Newton's second law states that a force ''F'' applied to a mass ''m'' produces an acceleration ''a'' given by the equation . Newton then posed the question: what must the force be that produces the elliptical orbits seen by Kepler? His answer came in his law of universal gravitation, which states that the force between a mass ''M'' and another mass ''m'' is given by the formula
where ''r'' is the distance between the masses and ''G'' is the gravitational constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's general relativity, theory of general relativity. It ...
. Given this force law and his equations of motion, Newton was able to show that two point masses attracting each other would each follow perfectly elliptical orbits. The ratio of sizes of these ellipses is ''m''/''M'', with the larger mass moving on a smaller ellipse. If ''M'' is much larger than ''m'', then the larger mass will appear to be stationary at the focus of the elliptical orbit of the lighter mass ''m''. This model can be applied approximately to the Solar System. Since the mass of the Sun is much larger than those of the planets, the force acting on each planet is principally due to the Sun; the gravity of the planets for each other can be neglected to first approximation.
Apsidal precession
 If the potential energy between the two bodies is not exactly the 1/''r'' potential of Newton's gravitational law but differs only slightly, then the ellipse of the orbit gradually rotates (among other possible effects). This
If the potential energy between the two bodies is not exactly the 1/''r'' potential of Newton's gravitational law but differs only slightly, then the ellipse of the orbit gradually rotates (among other possible effects). This apsidal precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsis, apsides (line of apsides) of an orbiting body, astronomical body's orbit. The apsides are the orbital poi ...
is observed for all the planets orbiting the Sun, primarily due to the oblateness of the Sun (it is not perfectly spherical) and the attractions of the other planets to one another. The apsides are the two points of closest and furthest distance of the orbit (the periapsis and apoapsis, respectively); apsidal precession corresponds to the rotation of the line joining the apsides. It also corresponds to the rotation of the Laplace–Runge–Lenz vector
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector (geometric), vector used chiefly to describe the shape and orientation of the orbit (celestial mechanics), orbit of one astronomical body around another, such as a ...
, which points along the line of apsides.
Newton's law of gravitation soon became accepted because it gave very accurate predictions of the motion of all the planets. These calculations were carried out initially by Pierre-Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
in the late 18th century, and refined by Félix Tisserand in the later 19th century. Conversely, if Newton's law of gravitation did ''not'' predict the apsidal precessions of the planets accurately, it would have to be discarded as a theory of gravitation. Such an anomalous precession was observed in the second half of the 19th century.
Anomalous precession of Mercury
 In 1859,
In 1859, Urbain Le Verrier
Urbain Jean Joseph Le Verrier (; 11 March 1811 – 23 September 1877) was a French astronomer and mathematician who specialized in celestial mechanics and is best known for predicting the existence and position of Neptune using only mathematics. ...
discovered that the orbital precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
of the planet Mercury was not quite what it should be; the ellipse of its orbit was rotating (precessing) slightly faster than predicted by the traditional theory of Newtonian gravity, even after all the effects of the other planets had been accounted for. The effect is small (roughly 43 arcsecond
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a tu ...
s of rotation per century), but well above the measurement error (roughly 0.1 arcsecond
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a tu ...
s per century). Le Verrier realized the importance of his discovery immediately, and challenged astronomers and physicists alike to account for it. Several classical explanations were proposed, such as interplanetary dust, unobserved oblateness of the Sun
The Sun is the star at the centre of the Solar System. It is a massive, nearly perfect sphere of hot plasma, heated to incandescence by nuclear fusion reactions in its core, radiating the energy from its surface mainly as visible light a ...
, an undetected moon of Mercury, or a new planet named Vulcan. After these explanations were discounted, some physicists were driven to the more radical hypothesis that Newton's inverse-square law
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental ca ...
of gravitation was incorrect. For example, some physicists proposed a power law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the ...
with an exponent
In mathematics, exponentiation, denoted , is an operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, i ...
that was slightly different from 2.
Others argued that Newton's law should be supplemented with a velocity-dependent potential. However, this implied a conflict with Newtonian celestial dynamics. In his treatise on celestial mechanics, Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
had shown that if the gravitational influence does not act instantaneously, then the motions of the planets themselves will not exactly conserve momentum (and consequently some of the momentum would have to be ascribed to the mediator of the gravitational interaction, analogous to ascribing momentum to the mediator of the electromagnetic interaction.) As seen from a Newtonian point of view, if gravitational influence does propagate at a finite speed, then at all points in time a planet is attracted to a point where the Sun was some time before, and not towards the instantaneous position of the Sun. On the assumption of the classical fundamentals, Laplace had shown that if gravity would propagate at a velocity on the order of the speed of light then the solar system would be unstable, and would not exist for a long time. The observation that the solar system is old enough allowed him to put a lower limit on the speed of gravity that turned out to be many orders of magnitude faster than the speed of light.
Laplace's estimate for the speed of gravity is not correct in a field theory which respects the principle of relativity. Since electric and magnetic fields combine, the attraction of a point charge which is moving at a constant velocity is towards the extrapolated instantaneous position, not to the apparent position it seems to occupy when looked at.''Feynman Lectures on Physics vol. II'' gives a thorough treatment of the analogous problem in electromagnetism. Feynman shows that for a moving charge, the non-radiative field is an attraction/repulsion not toward the apparent position of the particle, but toward the extrapolated position assuming that the particle continues in a straight line in a constant velocity. This is a notable property of the Liénard–Wiechert potentials which are used in the Wheeler–Feynman absorber theory
The Wheeler–Feynman absorber theory (also called the Wheeler–Feynman time-symmetric theory), named after its originators, the physicists Richard Feynman and John Archibald Wheeler, is a theory of electrodynamics based on a relativistic correct ...
. Presumably the same holds in linearized gravity: e.g., see Gravitoelectromagnetism. To avoid those problems, between 1870 and 1900 many scientists used the electrodynamic laws of Wilhelm Eduard Weber
Wilhelm Eduard Weber ( ; ; 24 October 1804 – 23 June 1891) was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.
Biography
Early years
Weber was born in Schlossstrasse in Witte ...
, Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
, Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
to produce stable orbits and to explain the perihelion shift of Mercury's orbit. In 1890, Maurice Lévy succeeded in doing so by combining the laws of Weber and Riemann, whereby the speed of gravity is equal to the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
in his theory. And in another attempt Paul Gerber
Paul Gerber (1854 Berlin, Germany – 13 August 1909 Freiburg im Breisgau, Germany) was a German physics teacher. He studied in Berlin from 1872 to 1875. In 1877 he became a teacher at the Realgymnasium (high school) in Stargard in Pommern. Ge ...
(1898) even succeeded in deriving the correct formula for the perihelion shift (which was identical to that formula later used by Einstein). However, because the basic laws of Weber and others were wrong (for example, Weber's law was superseded by Maxwell's theory), those hypotheses were rejected. Another attempt by Hendrik Lorentz
Hendrik Antoon Lorentz ( ; ; 18 July 1853 – 4 February 1928) was a Dutch theoretical physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for their discovery and theoretical explanation of the Zeeman effect. He derive ...
(1900), who already used Maxwell's theory, produced a perihelion shift which was too low.
Einstein's theory of general relativity
 Around 1904–1905, the works of
Around 1904–1905, the works of Hendrik Lorentz
Hendrik Antoon Lorentz ( ; ; 18 July 1853 – 4 February 1928) was a Dutch theoretical physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for their discovery and theoretical explanation of the Zeeman effect. He derive ...
, Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
and finally Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
's special theory of relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 paper,
"On the Electrodynamics of Moving Bodies", the theory is presen ...
, exclude the possibility of propagation of any effects faster than the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
. It followed that Newton's law of gravitation would have to be replaced with another law, compatible with the principle of relativity, while still obtaining the Newtonian limit for circumstances where relativistic effects are negligible. Such attempts were made by Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
(1905), Hermann Minkowski
Hermann Minkowski (22 June 1864 – 12 January 1909) was a mathematician and professor at the University of Königsberg, the University of Zürich, and the University of Göttingen, described variously as German, Polish, Lithuanian-German, o ...
(1907) and Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld (; 5 December 1868 – 26 April 1951) was a German Theoretical physics, theoretical physicist who pioneered developments in Atomic physics, atomic and Quantum mechanics, quantum physics, and also educated and ...
(1910). In 1907 Einstein came to the conclusion that to achieve this a successor to special relativity was needed. From 1907 to 1915, Einstein worked towards a new theory, using his equivalence principle
The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same t ...
as a key concept to guide his way. According to this principle, a uniform gravitational field acts equally on everything within it and, therefore, cannot be detected by a free-falling observer. Conversely, all local gravitational effects should be reproducible in a linearly accelerating reference frame, and vice versa. Thus, gravity acts like a fictitious force
A fictitious force, also known as an inertial force or pseudo-force, is a force that appears to act on an object when its motion is described or experienced from a non-inertial reference frame, non-inertial frame of reference. Unlike real forc ...
such as the centrifugal force
Centrifugal force is a fictitious force in Newtonian mechanics (also called an "inertial" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It appears to be directed radially away from the axi ...
or the Coriolis force
In physics, the Coriolis force is a pseudo force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motio ...
, which result from being in an accelerated reference frame; all fictitious forces are proportional to the inertial mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary parti ...
, just as gravity is. To effect the reconciliation of gravity and special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
and to incorporate the equivalence principle, something had to be sacrificed; that something was the long-held classical assumption that our space obeys the laws of Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, e.g., that the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
is true experimentally. Einstein used a more general geometry, pseudo-Riemannian geometry, to allow for the curvature of space and time that was necessary for the reconciliation; after eight years of work (1907–1915), he succeeded in discovering the precise way in which space-time
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three-dimensional space, three dimensions of space and the one dimension of time into a single four-dimensional continuum (measurement), continu ...
should be curved in order to reproduce the physical laws observed in Nature, particularly gravitation. Gravity is distinct from the fictitious forces centrifugal force and coriolis force in the sense that the curvature of spacetime is regarded as physically real, whereas the fictitious forces are not regarded as forces. The very first solutions of his field equations explained the anomalous precession of Mercury and predicted an unusual bending of light, which was confirmed ''after'' his theory was published. These solutions are explained below.
General relativity, special relativity and geometry
In the normalEuclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, triangles obey the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, which states that the square distance ''ds''2 between two points in space is the sum of the squares of its perpendicular components
where ''dx'', ''dy'' and ''dz'' represent the infinitesimal differences between the ''x'', ''y'' and ''z'' coordinates of two points in a Cartesian coordinate system
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative number ...
. Now imagine a world in which this is not quite true; a world where the distance is instead given by
where ''F'', ''G'' and ''H'' are arbitrary functions of position. It is not hard to imagine such a world; we live on one. The surface of the earth is curved, which is why it is impossible to make a perfectly accurate flat map of the earth. Non-Cartesian coordinate systems illustrate this well; for example, in the spherical coordinates (''r'', ''θ'', ''φ''), the Euclidean distance can be written
Another illustration would be a world in which the rulers used to measure length were untrustworthy, rulers that changed their length with their position and even their orientation. In the most general case, one must allow for cross-terms when calculating the distance ''ds''
where the nine functions ''g''xx, ''g''xy, ..., ''g''zz constitute the metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
, which defines the geometry of the space in Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as manifold, smooth manifolds with a ''Riemannian metric'' (an inner product on the tangent space at each point that varies smooth function, smo ...
. In the spherical-coordinates example above, there are no cross-terms; the only nonzero metric tensor components are ''g''rr = 1, ''g''θθ = ''r''2 and ''g''φφ = ''r''2 sin2 θ.
In his special theory of relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 paper,
"On the Electrodynamics of Moving Bodies", the theory is presen ...
, Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
showed that the distance ''ds'' between two spatial points is not constant, but depends on the motion of the observer. However, there is a measure of separation between two points in space-time
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three-dimensional space, three dimensions of space and the one dimension of time into a single four-dimensional continuum (measurement), continu ...
— called "proper time" and denoted with the symbol dτ — that ''is'' invariant; in other words, it does not depend on the motion of the observer.
which may be written in spherical coordinates as
This formula is the natural extension of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
and similarly holds only when there is no curvature in space-time. In general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
, however, space and time may have curvature, so this distance formula must be modified to a more general form
just as we generalized the formula to measure distance on the surface of the Earth. The exact form of the metric ''g''''μν'' depends on the gravitating mass, momentum and energy, as described by the Einstein field equations
In the General relativity, general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of Matter#In general relativity and cosmology, matter within it. ...
. Einstein developed those field equations to match the then known laws of Nature; however, they predicted never-before-seen phenomena (such as the bending of light by gravity) that were confirmed later.
Geodesic equation
According to Einstein's theory of general relativity, particles of negligible mass travel alonggeodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
s in the space-time. In uncurved space-time, far from a source of gravity, these geodesics correspond to straight lines; however, they may deviate from straight lines when the space-time is curved. The equation for the geodesic lines is
where Γ represents the Christoffel symbol and the variable ''q'' parametrizes the particle's path through space-time
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three-dimensional space, three dimensions of space and the one dimension of time into a single four-dimensional continuum (measurement), continu ...
, its so-called world line
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept of modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
. The Christoffel symbol depends only on the metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
''g''μν, or rather on how it changes with position. The variable ''q'' is a constant multiple of the proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. The proper time interval between two events on a world line is the change in proper time ...
''τ'' for timelike orbits (which are traveled by massive particles), and is usually taken to be equal to it. For lightlike (or null) orbits (which are traveled by massless particles such as the photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
), the proper time is zero and, strictly speaking, cannot be used as the variable ''q''. Nevertheless, lightlike orbits can be derived as the ultrarelativistic limit of timelike orbits, that is, the limit as the particle mass ''m'' goes to zero while holding its total energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
fixed.
Schwarzschild solution
An exact solution to theEinstein field equations
In the General relativity, general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of Matter#In general relativity and cosmology, matter within it. ...
is the Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumpti ...
, which corresponds to the external gravitational field of a stationary, uncharged, non-rotating, spherically symmetric body of mass ''M''. It is characterized by a length scale ''r''s, known as the Schwarzschild radius, which is defined by the formula
where ''G'' is the gravitational constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's general relativity, theory of general relativity. It ...
. The classical Newtonian theory of gravity is recovered in the limit as the ratio ''r''s/''r'' goes to zero. In that limit, the metric returns to that defined by special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
.
In practice, this ratio is almost always extremely small. For example, the Schwarzschild radius ''r''s of the Earth is roughly 9 mm; at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The Schwarzschild radius of the Sun is much larger, roughly 2953 meters, but at its surface, the ratio ''r''s/''r'' is roughly 4 parts in a million. A white dwarf
A white dwarf is a Compact star, stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very density, dense: in an Earth sized volume, it packs a mass that is comparable to the Sun. No nuclear fusion takes place i ...
star is much denser, but even here the ratio at its surface is roughly 250 parts in a million. The ratio only becomes large close to ultra-dense objects such as neutron star
A neutron star is the gravitationally collapsed Stellar core, core of a massive supergiant star. It results from the supernova explosion of a stellar evolution#Massive star, massive star—combined with gravitational collapse—that compresses ...
s (where the ratio is roughly 50%) and black hole
A black hole is a massive, compact astronomical object so dense that its gravity prevents anything from escaping, even light. Albert Einstein's theory of general relativity predicts that a sufficiently compact mass will form a black hole. Th ...
s.
Orbits about the central mass
 The orbits of a test particle of infinitesimal mass about the central mass is given by the equation of motion
where is the
The orbits of a test particle of infinitesimal mass about the central mass is given by the equation of motion
where is the specific relative angular momentum
In celestial mechanics, the specific relative angular momentum (often denoted \vec or \mathbf) of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative positi ...
, and is the reduced mass
In physics, reduced mass is a measure of the effective inertial mass of a system with two or more particles when the particles are interacting with each other. Reduced mass allows the two-body problem to be solved as if it were a one-body probl ...
. This can be converted into an equation for the orbit
where, for brevity, two length-scales, and , have been introduced. They are constants of the motion and depend on the initial conditions (position and velocity) of the test particle. Hence, the solution of the orbit equation is
Effective radial potential energy
The equation of motion for the particle derived above can be rewritten using the definition of the Schwarzschild radius ''r''s as which is equivalent to a particle moving in a one-dimensionaleffective potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the "opposing" centrifugal potential energy with the potential energy of a ...
The first two terms are well-known classical energies, the first being the attractive Newtonian gravitational potential energy
Gravitational energy or gravitational potential energy is the potential energy an object with mass has due to the gravitational potential of its position in a gravitational field. Mathematically, it is the minimum Work (physics), mechanical work t ...
and the second corresponding to the repulsive "centrifugal" potential energy; however, the third term is an attractive energy unique to general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
. As shown below and elsewhere, this inverse-cubic energy causes elliptical orbits to precess gradually by an angle δφ per revolution
where ''A'' is the semi-major axis and ''e'' is the eccentricity. Here ''δφ'' is ''not'' the change in the ''φ''-coordinate in (''t'', ''r'', ''θ'', ''φ'') coordinates but the change in the argument of periapsis of the classical closed orbit.
The third term is attractive and dominates at small ''r'' values, giving a critical inner radius ''r''inner at which a particle is drawn inexorably inwards to ''r'' = 0; this inner radius is a function of the particle's angular momentum per unit mass or, equivalently, the ''a'' length-scale defined above.
Circular orbits and their stability
quadratic formula
In elementary algebra, the quadratic formula is a closed-form expression describing the solutions of a quadratic equation. Other ways of solving quadratic equations, such as completing the square, yield the same solutions.
Given a general quadr ...
. The inner radius ''r''inner is unstable, because the attractive third force strengthens much faster than the other two forces when ''r'' becomes small; if the particle slips slightly inwards from ''r''inner (where all three forces are in balance), the third force dominates the other two and draws the particle inexorably inwards to ''r'' = 0. At the outer radius, however, the circular orbits are stable; the third term is less important and the system behaves more like the non-relativistic Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attra ...
.
When ''a'' is much greater than ''r''s (the classical case), these formulae become approximately
centrifugal force
Centrifugal force is a fictitious force in Newtonian mechanics (also called an "inertial" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It appears to be directed radially away from the axi ...
equal to the Newtonian gravitational force:
where is the reduced mass
In physics, reduced mass is a measure of the effective inertial mass of a system with two or more particles when the particles are interacting with each other. Reduced mass allows the two-body problem to be solved as if it were a one-body probl ...
.
In our notation, the classical orbital angular speed equals
At the other extreme, when ''a''2 approaches 3''r''s2 from above, the two radii converge to a single value
The quadratic solutions above ensure that ''r''outer is always greater than 3''r''s, whereas ''r''inner lies between ''r''s and 3''r''s. Circular orbits smaller than ''r''s are not possible. For massless particles, ''a'' goes to infinity, implying that there is a circular orbit for photons at ''r''inner = ''r''s. The sphere of this radius is sometimes known as the photon sphere
A photon sphere, or photon ring or photon circle, arises in a neighbourhood of the event horizon of a black hole where gravity is so strong that emitted photons will not just bend around the black hole but also return to the point where they we ...
.
Precession of elliptical orbits
binomial theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and a ...
yields the formula
Multiplying by the period ''T'' of one revolution gives the precession of the orbit per revolution
where we have used ''ω''''φ''''T'' = 2 and the definition of the length-scale ''a''. Substituting the definition of the Schwarzschild radius ''r''s gives
This may be simplified using the elliptical orbit's semi-major axis ''A'' and eccentricity ''e'' related by the formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
to give the precession angle
Since the closed classical orbit is an ellipse in general, the quantity ''A''(1 − ''e''2) is the semi-latus rectum
A conic section, conic or a quadratic curve is a curve obtained from a Conical surface, cone's surface intersecting a plane (mathematics), plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is ...
''l'' of the ellipse.
Hence, the final formula of angular apsidal precession for a unit complete revolution is
Beyond the Schwarzschild solution

Post-Newtonian expansion
In the Schwarzschild solution, it is assumed that the larger mass ''M'' is stationary and it alone determines the gravitational field (i.e., the geometry of space-time) and, hence, the lesser mass ''m'' follows a geodesic path through that fixed space-time. This is a reasonable approximation for photons and the orbit of Mercury, which is roughly 6 million times lighter than the Sun. However, it is inadequate forbinary star
A binary star or binary star system is a system of two stars that are gravitationally bound to and in orbit around each other. Binary stars in the night sky that are seen as a single object to the naked eye are often resolved as separate stars us ...
s, in which the masses may be of similar magnitude.
The metric for the case of two comparable masses cannot be solved in closed form and therefore one has to resort to approximation techniques such as the post-Newtonian approximation or numerical approximations. In passing, we mention one particular exception in lower dimensions (see ''R'' = ''T'' model for details). In (1+1) dimensions, i.e. a space made of one spatial dimension and one time dimension, the metric for two bodies of equal masses can be solved analytically in terms of the Lambert W function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the Branch point, branches of the converse relation of the function , where is any complex number and is the expone ...
. However, the gravitational energy between the two bodies is exchanged via dilaton
In particle physics, the hypothetical dilaton is a particle of a scalar field \varphi that appears in theories with extra dimensions when the volume of the compactified dimensions varies. It appears as a radion in Kaluza–Klein theory's compa ...
s rather than gravitons
In theories of quantum gravity, the graviton is the hypothetical elementary particle that mediates the force of gravitational interaction. There is no complete quantum field theory of gravitons due to an outstanding mathematical problem with ren ...
which require three-space in which to propagate.
The post-Newtonian expansion
In general relativity, post-Newtonian expansions (PN expansions) are used for finding an approximate solution of Einstein field equations for the metric tensor (general relativity), metric tensor. The approximations are expanded in small paramet ...
is a calculational method that provides a series of ever more accurate solutions to a given problem. The method is iterative; an initial solution for particle motions is used to calculate the gravitational fields; from these derived fields, new particle motions can be calculated, from which even more accurate estimates of the fields can be computed, and so on. This approach is called "post-Newtonian" because the Newtonian solution for the particle orbits is often used as the initial solution.
The theory can be divided into two parts: first one finds the two-body effective potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the "opposing" centrifugal potential energy with the potential energy of a ...
that captures the GR corrections to the Newtonian potential. Secondly, one should solve the resulting equations of motion.
Modern computational approaches
Einstein's equations can also be solved on a computer using sophisticated numerical methods. Given sufficient computer power, such solutions can be more accurate than post-Newtonian solutions. However, such calculations are demanding because the equations must generally be solved in a four-dimensional space. Nevertheless, beginning in the late 1990s, it became possible to solve difficult problems such as the merger of two black holes, which is a very difficult version of the Kepler problem in general relativity.Gravitational radiation
If there is no incoming gravitational radiation, according togeneral relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
, two bodies orbiting one another will emit gravitational radiation
Gravitational waves are oscillations of the gravitational field that travel through space at the speed of light; they are generated by the relative motion of gravitating masses. They were proposed by Oliver Heaviside in 1893 and then later by ...
, causing the orbits to gradually lose energy.
The formulae describing the loss of energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
and angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
due to gravitational radiation from the two bodies of the Kepler problem have been calculated. The rate of losing energy (averaged over a complete orbit) is given by
where ''e'' is the orbital eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values be ...
and ''a'' is the semimajor axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the long ...
of the elliptical orbit. The angular brackets on the left-hand side of the equation represent the averaging over a single orbit. Similarly, the average rate of losing angular momentum equals
The rate of period decrease is given by
where ''P''''b'' is orbital period.
The losses in energy and angular momentum increase significantly as the eccentricity approaches one, i.e., as the ellipse of the orbit becomes ever more elongated. The radiation losses also increase significantly with a decreasing size ''a'' of the orbit.
periastron
An apsis (; ) is the farthest or nearest point in the orbit of a planetary-mass object, planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two maximum a ...
of the binary pulsar PSR B1913+16 (red dots) matches the change due to the reduction in orbital period predicted by general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
(blue curve) almost exactly.
File:Wavy2.gif, Two neutron stars rotating rapidly around one another gradually lose energy by emitting gravitational radiation. As they lose energy, they orbit each other more quickly and more closely to one another.
See also
* Binet equation * Center of mass (relativistic) * Gravitational two-body problem *Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attra ...
* Newton's theorem of revolving orbits
* Schwarzschild geodesics
Notes
References
Bibliography
* * * * * * * (See Gravitation (book).) * * * * * * * * *External links
Animation
showing relativistic precession of stars around the Milky Way supermassive black hole
from ''Reflections on Relativity'' by Kevin Brown. {{Relativity Exact solutions in general relativity