Tusi Couple on:
[Wikipedia]
[Google]
[Amazon]
The Tusi couple (also known as Tusi's mechanism) is a
 The translation of the copy of Tusi's original description of his geometrical model alludes to at least one inversion of the model to be seen in the diagrams:
:If two coplanar circles, the diameter of one of which is equal to half the diameter of the other, are taken to be internally tangent at a point, and if a point is taken on the smaller circle—and let it be at the point of tangency—and if the two circles move with simple motions in opposite direction in such a way that the motion of the smaller ircleis twice that of the larger so the smaller completes two rotations for each rotation of the larger, then that point will be seen to move on the diameter of the larger circle that initially passes through the point of tangency, oscillating between the endpoints.
Algebraically, the model can be expressed with complex numbers as
:
Other commentators have observed that the Tusi couple can be interpreted as a rolling curve where the rotation of the inner circle satisfies a no-slip condition as its tangent point moves along the fixed outer circle.
The translation of the copy of Tusi's original description of his geometrical model alludes to at least one inversion of the model to be seen in the diagrams:
:If two coplanar circles, the diameter of one of which is equal to half the diameter of the other, are taken to be internally tangent at a point, and if a point is taken on the smaller circle—and let it be at the point of tangency—and if the two circles move with simple motions in opposite direction in such a way that the motion of the smaller ircleis twice that of the larger so the smaller completes two rotations for each rotation of the larger, then that point will be seen to move on the diameter of the larger circle that initially passes through the point of tangency, oscillating between the endpoints.
Algebraically, the model can be expressed with complex numbers as
:
Other commentators have observed that the Tusi couple can be interpreted as a rolling curve where the rotation of the inner circle satisfies a no-slip condition as its tangent point moves along the fixed outer circle.
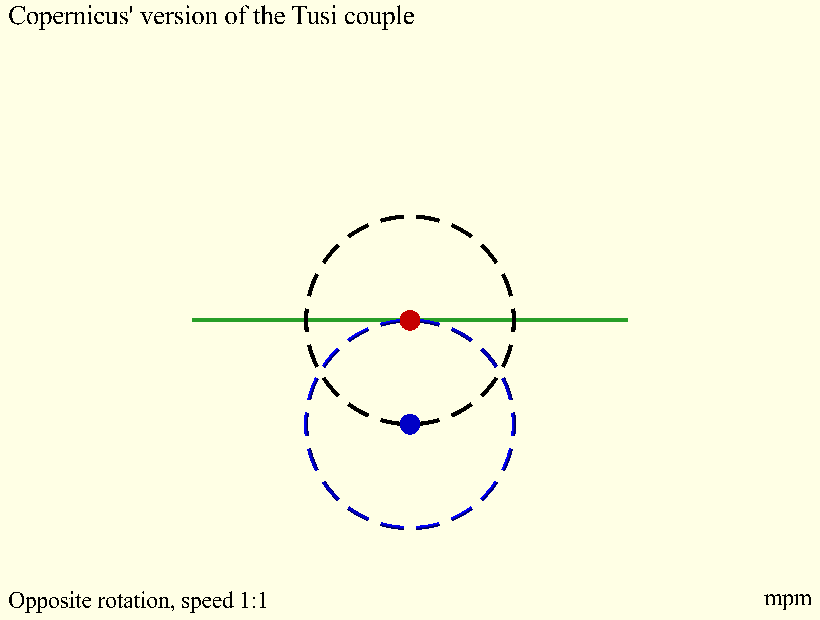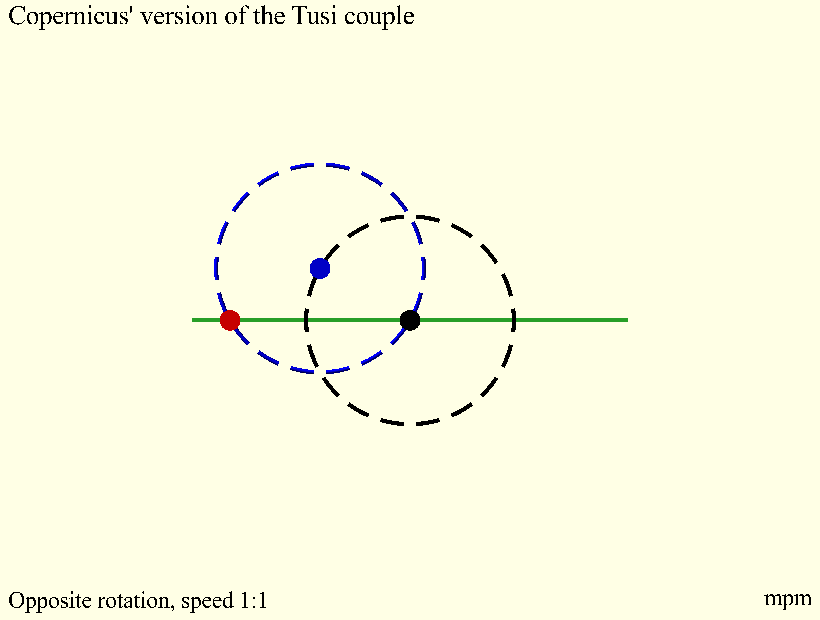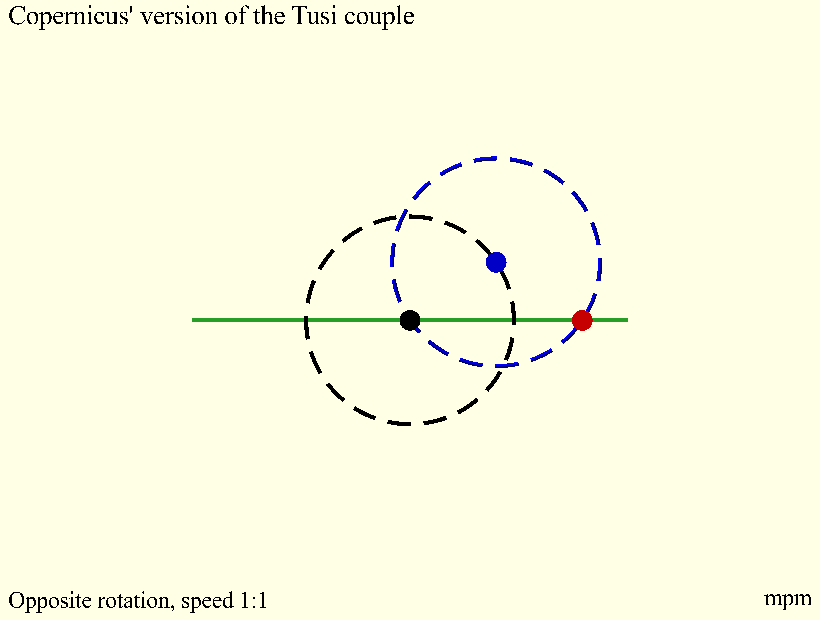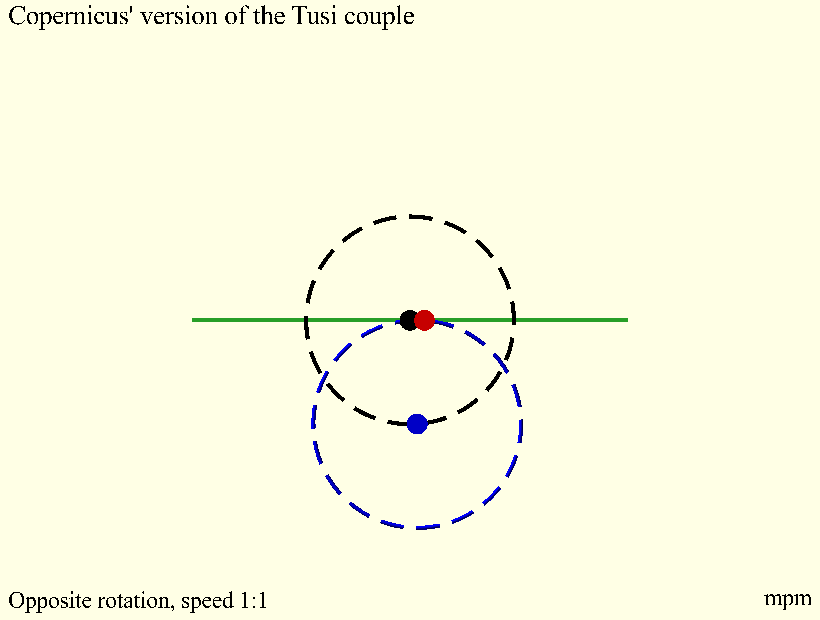 The term "Tusi couple" is a modern one, coined by Edward Stewart Kennedy in 1966. It is one of several late Islamic astronomical devices bearing a striking similarity to models in
The term "Tusi couple" is a modern one, coined by Edward Stewart Kennedy in 1966. It is one of several late Islamic astronomical devices bearing a striking similarity to models in
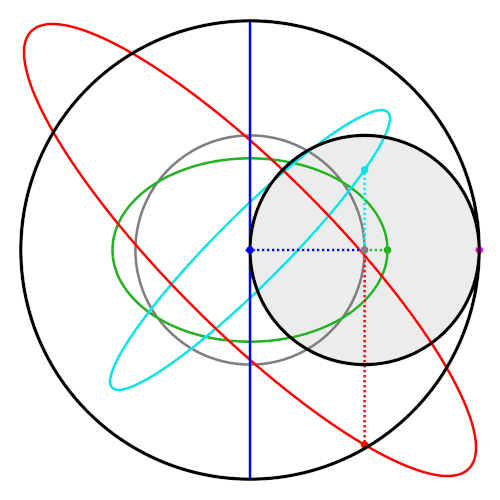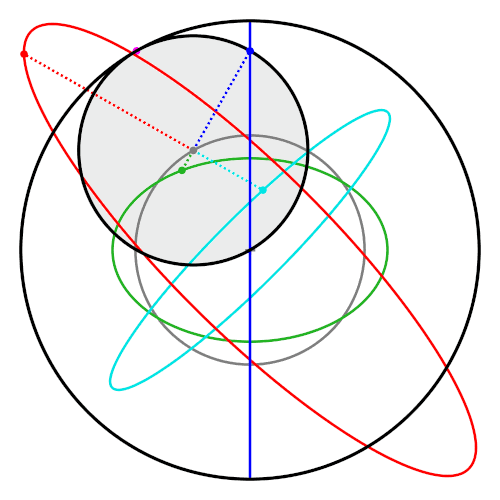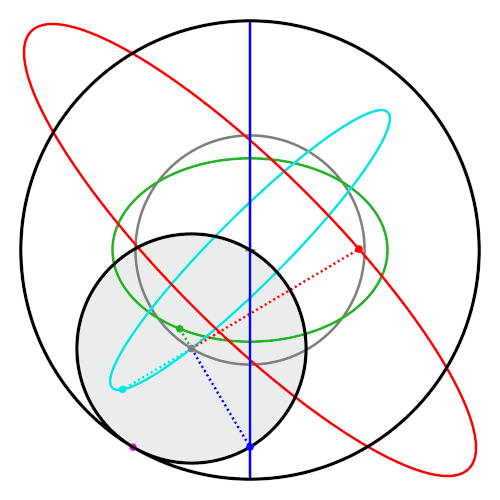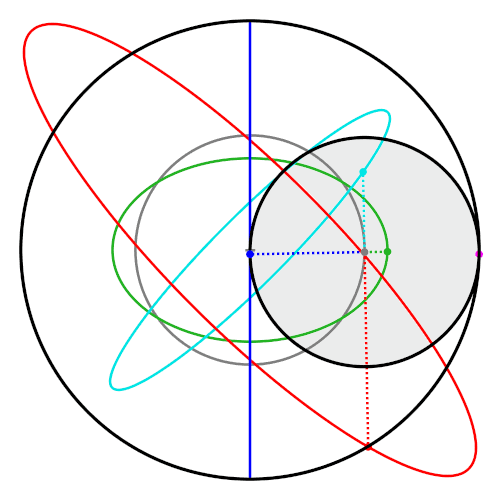 A property of the Tusi couple is that points on the inner circle that are not on the circumference trace
A property of the Tusi couple is that points on the inner circle that are not on the circumference trace
Ancient Planetary Model Animations
includes two links of interest: *
*
* George Saliba
Discusses the model of Nasir al-Din al-Tusi and the interactions of Arabic, Greek, and Latin astronomers. {{Islamic astronomy Astronomy in the medieval Islamic world Linear motion Roulettes (curve) 13th-century inventions
mathematical
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
device in which a small circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
rotates inside a larger circle twice the diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
of the smaller circle. Rotations of the circles cause a point on the circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
of the smaller circle to oscillate
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulu ...
back and forth in linear motion
Linear motion, also called rectilinear motion, is one-dimensional motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion, with ...
along a diameter of the larger circle. The Tusi couple is a two-cusped hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid creat ...
.
The couple was first proposed by the 13th-century Persian astronomer
An astronomer is a scientist in the field of astronomy who focuses on a specific question or field outside the scope of Earth. Astronomers observe astronomical objects, such as stars, planets, natural satellite, moons, comets and galaxy, galax ...
and mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematica ...
Nasir al-Din al-Tusi
Muḥammad ibn Muḥammad ibn al-Ḥasan al-Ṭūsī (1201 – 1274), also known as Naṣīr al-Dīn al-Ṭūsī (; ) or simply as (al-)Tusi, was a Persians, Persian polymath, architect, Early Islamic philosophy, philosopher, Islamic medicine, phy ...
in his 1247 ''Tahrir al-Majisti'' (''Commentary on the Almagest'') as a solution for the latitudinal motion of the inferior planets and later used extensively as a substitute for the equant introduced over a thousand years earlier in Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
's ''Almagest
The ''Almagest'' ( ) is a 2nd-century Greek mathematics, mathematical and Greek astronomy, astronomical treatise on the apparent motions of the stars and planetary paths, written by Ptolemy, Claudius Ptolemy ( ) in Koine Greek. One of the most i ...
''.
Original description
 The translation of the copy of Tusi's original description of his geometrical model alludes to at least one inversion of the model to be seen in the diagrams:
:If two coplanar circles, the diameter of one of which is equal to half the diameter of the other, are taken to be internally tangent at a point, and if a point is taken on the smaller circle—and let it be at the point of tangency—and if the two circles move with simple motions in opposite direction in such a way that the motion of the smaller ircleis twice that of the larger so the smaller completes two rotations for each rotation of the larger, then that point will be seen to move on the diameter of the larger circle that initially passes through the point of tangency, oscillating between the endpoints.
Algebraically, the model can be expressed with complex numbers as
:
Other commentators have observed that the Tusi couple can be interpreted as a rolling curve where the rotation of the inner circle satisfies a no-slip condition as its tangent point moves along the fixed outer circle.
The translation of the copy of Tusi's original description of his geometrical model alludes to at least one inversion of the model to be seen in the diagrams:
:If two coplanar circles, the diameter of one of which is equal to half the diameter of the other, are taken to be internally tangent at a point, and if a point is taken on the smaller circle—and let it be at the point of tangency—and if the two circles move with simple motions in opposite direction in such a way that the motion of the smaller ircleis twice that of the larger so the smaller completes two rotations for each rotation of the larger, then that point will be seen to move on the diameter of the larger circle that initially passes through the point of tangency, oscillating between the endpoints.
Algebraically, the model can be expressed with complex numbers as
:
Other commentators have observed that the Tusi couple can be interpreted as a rolling curve where the rotation of the inner circle satisfies a no-slip condition as its tangent point moves along the fixed outer circle.
Other sources
 The term "Tusi couple" is a modern one, coined by Edward Stewart Kennedy in 1966. It is one of several late Islamic astronomical devices bearing a striking similarity to models in
The term "Tusi couple" is a modern one, coined by Edward Stewart Kennedy in 1966. It is one of several late Islamic astronomical devices bearing a striking similarity to models in Nicolaus Copernicus
Nicolaus Copernicus (19 February 1473 – 24 May 1543) was a Renaissance polymath who formulated a mathematical model, model of Celestial spheres#Renaissance, the universe that placed heliocentrism, the Sun rather than Earth at its cen ...
's '' De revolutionibus'', including his Mercury model and his theory of trepidation. Historians suspect that Copernicus or another European author had access to an Arabic astronomical text, but an exact chain of transmission has not yet been identified, The 16th century scientist and traveler Guillaume Postel has been suggested as one possible facilitator.
Since the Tusi-couple was used by Copernicus in his reformulation of mathematical astronomy, there is a growing consensus that he became aware of this idea in some way. It has been suggested that the idea of the Tusi couple may have arrived in Europe leaving few manuscript traces, since it could have occurred without the translation of any Arabic text into Latin. One possible route of transmission may have been through Byzantine science; Gregory Chioniades translated some of al-Tusi's works from Arabic into Byzantine Greek
Medieval Greek (also known as Middle Greek, Byzantine Greek, or Romaic; Greek: ) is the stage of the Greek language between the end of classical antiquity in the 5th–6th centuries and the end of the Middle Ages, conventionally dated to the F ...
. Several Byzantine Greek manuscripts containing the Tusi-couple are still extant in Italy. Another possibility is that he encountered the manuscript of the "Straightening of the Curves" (Sefer Meyasher 'Aqov) while studying in Italy.
While al-Tusi's model shows how a rectilinear motion can be obtained from two circular ones, Proclus's ''Commentary on the First Book of Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
'' shows, on the contrary, how a cyclic motion can be obtained from two rectilinear ones. In his ''questiones'' on the ''Sphere'' (written before 1362), Nicole Oresme described how to combine circular motions to produce a reciprocating linear motion of a planet along the radius of its epicycle. Oresme's description is unclear and it is not certain whether this represents an independent invention or an attempt to come to grips with a poorly understood Arabic text.
Later examples
Although the Tusi couple was developed within an astronomical context, later mathematicians and engineers developed similar versions of what came to be calledhypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid creat ...
straight-line mechanisms. The mathematician Gerolamo Cardano
Gerolamo Cardano (; also Girolamo or Geronimo; ; ; 24 September 1501– 21 September 1576) was an Italian polymath whose interests and proficiencies ranged through those of mathematician, physician, biologist, physicist, chemist, astrologer, as ...
designed a system known as ''Cardan's movement'' (also known as a ''Cardan gear''). Nineteenth-century engineers James White, Matthew Murray
Matthew Murray (1765 – 20 February 1826) was an English steam engine and machine tool manufacturer, who designed and built the first commercially viable steam locomotive, the twin-cylinder ''Salamanca'' in 1812. He was an innovative design ...
, as well as later designers, developed practical applications of the hypocycloid straight-line mechanism.
A practical and mechanically simple version of the Tusi couple, which avoids the use of an external rim gear, was developed in 2021 by John Goodman in order to provide linear motion. It uses 3 standard spur gears. A rotating (blue) arm is mounted on a central shaft, to which a fixed (yellow) gear is mounted. A (red) idler gear on the arm meshes with the fixed gear. A third (green) gear meshes with the idler. The third gear has half the number of teeth of the fixed gear. An (orange) arm is fixed to the third gear. If the length of the arm equals the distance between the fixed and outer gears = d, the arm will describe a straight line of throw = 2d. An advantage of this design is that, if standard modulus gears that do not provide the required throw, the idler gear does not have to be colinear with the other two gears
Hypotrochoid
 A property of the Tusi couple is that points on the inner circle that are not on the circumference trace
A property of the Tusi couple is that points on the inner circle that are not on the circumference trace ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
s. These ellipses, and the straight line traced by the classic Tusi couple, are special cases of hypotrochoid
In geometry, a hypotrochoid is a roulette (curve), roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle.
The par ...
s.
See also
* Murray's Hypocycloidal Engine, utilising a Tusi couple as a substitute for crosshead guides orparallel motion
Parallel may refer to:
Mathematics
* Parallel (geometry), two lines in the Euclidean plane which never intersect
* Parallel (operator), mathematical operation named after the composition of electrical resistance in parallel circuits
Science a ...
* Epicyclic gearing
An epicyclic gear train (also known as a planetary gearset) is a gear reduction assembly consisting of two gears mounted so that the center of one gear (the "planet") revolves around the center of the other (the "sun"). A carrier connects the ...
* Straight-line mechanism
* Spirograph
* Geometric lathe
* Guilloché
* Deltoid curve
Notes
References
* * * * Ragep, F. J. "The Two Versions of the Tusi Couple," in ''From Deferent to Equant: A Volume of Studies in the History of Science in Ancient and Medieval Near East in Honor of E. S. Kennedy'', ed. David King and George Saliba, Annals of the New York Academy of Sciences, 500. New York Academy of Sciences, 1987. (pbk.) * Ragep, F. J. ''Nasir al-Din al-Tusi's "Memoir on Astronomy,"'' Sources in the History of Mathematics and Physical Sciences,12. 2 vols. Berlin/New York: Springer, 1993. / .External links
* Dennis W. DukeAncient Planetary Model Animations
includes two links of interest: *
*
* George Saliba
Discusses the model of Nasir al-Din al-Tusi and the interactions of Arabic, Greek, and Latin astronomers. {{Islamic astronomy Astronomy in the medieval Islamic world Linear motion Roulettes (curve) 13th-century inventions