Truncated Rhombic Dodecahedron

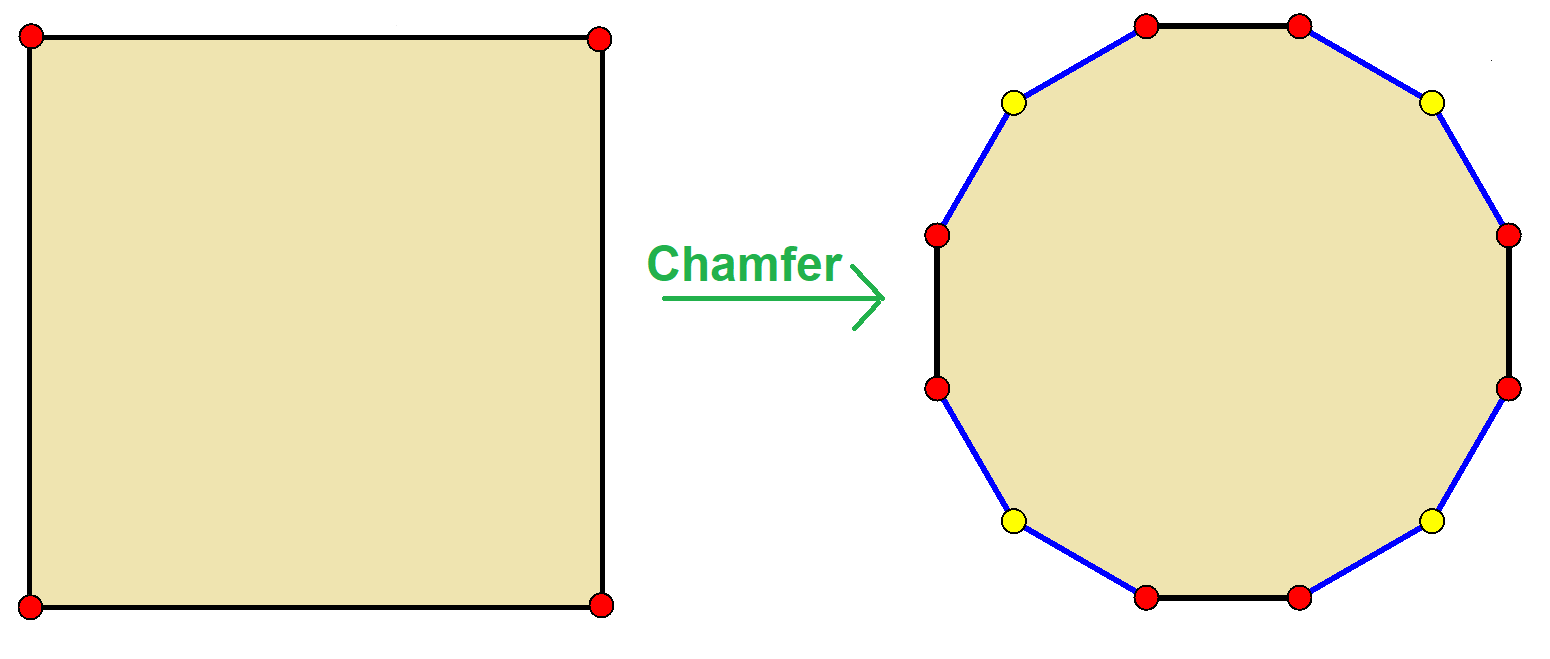
In geometry, a chamfer or edge-truncation is a topological operator that modifies one polyhedron into another. It separates the faces by reducing them, and adds a new face between each two adjacent faces (moving the vertices inward). Oppositely, similar to expansion, it moves the faces apart outward, and adds a new face between each two adjacent faces; but contrary to expansion, it maintains the original vertices.

For a polyhedron, this operation adds a new hexagonal face in place of each original edge.

In Conway polyhedron notation, ''chamfering'' is represented by the letter "c". A polyhedron with edges will have a chamfered form containing new vertices, new edges, and new hexagonal faces.

Chamfered Platonic solids

Chamfers of five Platonic solids are described in detail below. Each is shown in an equilateral version where all edges have the same length, and in a canonical version where all edges touch the same midsphere. The shown dual polyhedra are dual to the canonical versions.

Chamfered tetrahedron

The chamfered tetrahedron or alternate truncated cube is a convex polyhedron constructed:
* by chamfering a regular tetrahedron: replacing its 6 edges with congruent flattened hexagons;
* or by alternately truncating a (regular) cube: replacing 4 of its 8 vertices with congruent equilateral-triangle faces.
For a certain depth of chamfering/truncation, all (final) edges of the cT have the same length; then, the hexagons are equilateral, but not regular.

The dual of the ''chamfered tetrahedron'' is the alternate-triakis tetratetrahedron.

The cT is the Goldberg polyhedron GP_III(2,0) or _2,0, containing triangular and hexagonal faces.

Chamfered cube

The chamfered cube is constructed as a chamfer of a cube: the squares are reduced in size and new faces, hexagons, are added in place of all the original edges. The cC is a convex polyhedron with 32 vertices, 48 edges, and 18 faces: 6 congruent (and regular) squares, and 12 congruent flattened hexagons.
For a certain depth of chamfering, all (final) edges of the ''chamfered cube'' have the same length; then, the hexagons are equilateral, but not regular. They are congruent alternately truncated rhombi, have 2 internal angles of $\cos^(-\frac) \approx 109.47 ^\circ$ and 4 internal angles of $\pi - \frac \cos^(-\frac) \approx 125.26 ^\circ,$ while a regular hexagon would have all $120 ^\circ$ internal angles.

The cC is also inaccurately called a truncated rhombic dodecahedron, although that name rather suggests a rhombicuboctahedron. The cC can more accurately be called a tetratruncated rhombic dodecahedron, because only the (6) order-4 vertices of the rhombic dodecahedron are truncated.

The dual of the ''chamfered cube'' is the tetrakis cuboctahedron.

Because all the faces of the cC have an even number of sides and are centrally symmetric, it is a zonohedron:

GP_IV(2,0) or _2,0, containing square and hexagonal faces.

of a rhombic dodecahedron and a cube of edge length 1 when the eight order-3 vertices of the rhombic dodecahedron are at $(\pm 1, \pm 1, \pm 1)$ and its six order-4 vertices are at the permutations of $(\pm \sqrt 3, 0, 0).$

A topological equivalent to the ''chamfered cube'', but with pyritohedral symmetry and rectangular faces, can be constructed by chamfering the axial edges of a pyritohedron. This occurs in pyrite crystals.

Uses

The DaYan Gem 7 is a twisty puzzle in the shape of a chamfered cube.

Chamfered octahedron

The chamfered octahedron is a convex polyhedron constructed by truncating the 8 order-3 vertices of the rhombic dodecahedron. These truncated vertices become congruent equilateral triangles, and the original 12 rhombic faces become congruent flattened hexagons.
For a certain depth of truncation, all (final) edges of the cO have the same length; then, the hexagons are equilateral, but not regular.

The ''chamfered octahedron'' can also be called a tritruncated rhombic dodecahedron.

The dual of the cO is the triakis cuboctahedron.

Chamfered dodecahedron

The chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 12 congruent regular pentagons and 30 congruent flattened hexagons.
It is constructed as a chamfer of a regular dodecahedron. The pentagons are reduced in size and new faces, flattened hexagons, are added in place of all the original edges. For a certain depth of chamfering, all (final) edges of the cD have the same length; then, the hexagons are equilateral, but not regular.

The cD is also inaccurately called a truncated rhombic triacontahedron, although that name rather suggests a rhombicosidodecahedron. The cD can more accurately be called a pentatruncated rhombic triacontahedron, because only the (12) order-5 vertices of the rhombic triacontahedron are truncated.

The dual of the ''chamfered dodecahedron'' is the pentakis icosidodecahedron.

The cD is the Goldberg polyhedron GP_V(2,0) or _2,0, containing pentagonal and hexagonal faces.

Chamfered icosahedron

The chamfered icosahedron is a convex polyhedron constructed by truncating the 20 order-3 vertices of the rhombic triacontahedron. The hexagonal faces of the cI can be made equilateral, but not regular, with a certain depth of truncation.

The ''chamfered icosahedron'' can also be called a tritruncated rhombic triacontahedron.

The dual of the cI is the triakis icosidodecahedron.

Chamfered regular tilings

Relation to Goldberg polyhedra

The chamfer operation applied in series creates progressively larger polyhedra with new faces, hexagonal, replacing the edges of the current one. The chamfer operator transforms GP(m,n) to GP(2m,2n).

A regular polyhedron, GP(1,0), creates a Goldberg polyhedra sequence: GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...

The truncated octahedron or truncated icosahedron, GP(1,1), creates a Goldberg sequence: GP(1,1), GP(2,2), GP(4,4), GP(8,8)...

A truncated tetrakis hexahedron or pentakis dodecahedron, GP(3,0), creates a Goldberg sequence: GP(3,0), GP(6,0), GP(12,0)...

Chamfered polytopes and honeycombs

Like the expansion operation, chamfer can be applied to any dimension.

For polygons, it triples the number of vertices. Example:
:

For polychora, new cells are created around the original edges. The cells are prisms, containing two copies of the original face, with pyramids augmented onto the prism sides. ^{omething may be wrong in this passage/span>}

See also

* Conway polyhedron notation
* Near-miss Johnson solid
* Cantellation (geometry)

References

Sources

*
* Joseph D. Clinton, ''Clinton’s Equal Central Angle Conjecture'

*
*
* Antoine Deza, Michel Deza, Viatcheslav Grishukhin, ''Fullerenes and coordination polyhedra versus half-cube embeddings'', 1998 PDFbr>
(p. 72 Fig. 26. Chamfered tetrahedron)
* .
* {{cite EB1911, wstitle= Crystallography , volume= 07 , pages= 569–591 , last1= Spencer , first1= Leonard James , author-link= Leonard James Spencer

External links

Chamfered Tetrahedron




Livio Zefiro
* ttp://www.georgehart.com/virtual-polyhedra/conway_notation.html VRML polyhedral generator(Conway polyhedron notation)
** VRML mode
Chamfered cube


,6fullerene
* Fullerene C80
*

(Number 7 -Ih)
*


How to make a chamfered cube

Goldberg polyhedra
Polyhedra
Mathematical notation