Trapezoidal on:
[Wikipedia]
[Google]
[Amazon]
In
 An
An
 Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent
Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent
 The trapezoidal number is a set of
The trapezoidal number is a set of
"Trapezium"
at the ''
Trapezoid definition
(with interactive animations)
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
' (2008) {{Polygons Elementary shapes Types of quadrilaterals
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a trapezoid () in North American English
North American English (NAmE) encompasses the English language as spoken in both the United States and Canada. Because of their related histories and cultures, plus the similarities between the pronunciations (accents), vocabulary, and grammar ...
, or trapezium () in British English
British English is the set of Variety (linguistics), varieties of the English language native to the United Kingdom, especially Great Britain. More narrowly, it can refer specifically to the English language in England, or, more broadly, to ...
, is a quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
that has at least one pair of parallel sides.
The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...
, then the choice of bases and legs is arbitrary.)
A trapezoid is usually considered to be a convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
quadrilateral in Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids.
Definitions
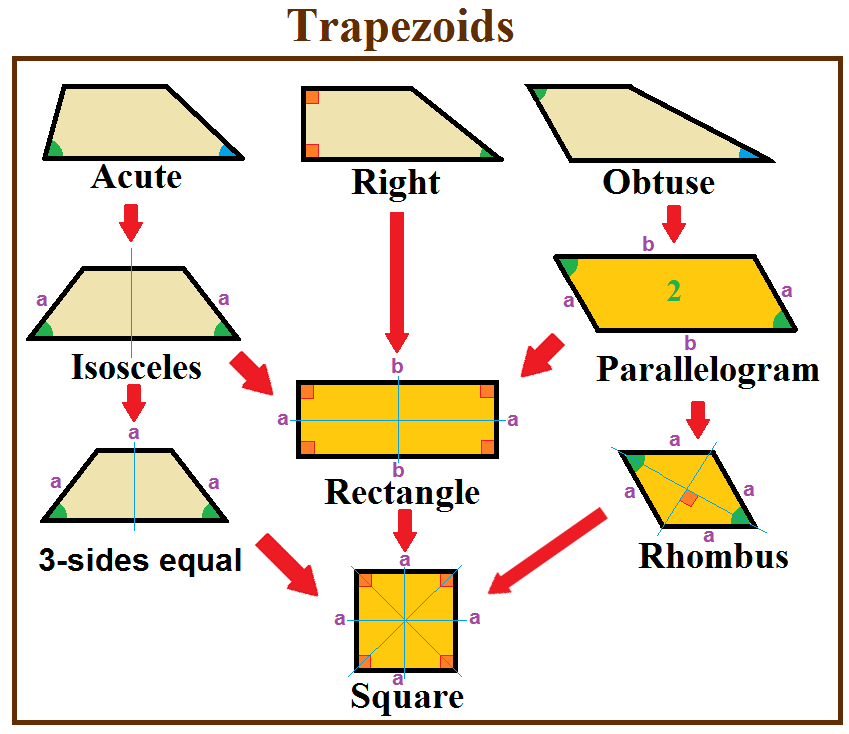
''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is any quadrilateral with one pair of parallel sides. In an inclusive classification scheme, definitions are hierarchical: a square is a type of rectangle and a type of rhombus, a rectangle or rhombus is a type of parallelogram, and every parallelogram is a type of trapezoid. Professional mathematicians andpost-secondary
Tertiary education (higher education, or post-secondary education) is the educational level following the completion of secondary education.
The World Bank defines tertiary education as including universities, colleges, and vocational schools ...
geometry textbooks nearly always prefer inclusive definitions and classifications, because they simplify statements and proofs of geometric theorems. In primary and secondary education, definitions of ''rectangle'' and ''parallelogram'' are also nearly always inclusive, but an exclusive definition of ''trapezoid'' is commonly found. This article uses the inclusive definition and considers parallelograms to be special kinds of trapezoids. (Cf. .)
To avoid confusion, some sources use the term ''proper trapezoid'' to describe trapezoids with exactly one pair of parallel sides, analogous to uses of the word ''proper'' in some other mathematical objects.
Etymology
In the ancient Greek geometry of Euclid's ''Elements'' ( BC), quadrilaterals were classified into exclusive categories:square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
; oblong (non-square rectangle
In Euclidean geometry, Euclidean plane geometry, a rectangle is a Rectilinear polygon, rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that a ...
); (non-square) rhombus
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhom ...
; rhomboid, meaning a non-rhombus non-rectangle parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...
; or trapezium (τραπέζιον, literally "table"), meaning any quadrilateral not already included in the previous categories.
The Neoplatonist philosopher Proclus
Proclus Lycius (; 8 February 412 – 17 April 485), called Proclus the Successor (, ''Próklos ho Diádokhos''), was a Greek Neoplatonist philosopher, one of the last major classical philosophers of late antiquity. He set forth one of th ...
(mid 5th century AD) wrote an influential commentary on Euclid with a richer set of categories, which he attributed to Posidonius
Posidonius (; , "of Poseidon") "of Apameia" (ὁ Ἀπαμεύς) or "of Rhodes" (ὁ Ῥόδιος) (), was a Greeks, Greek politician, astronomer, astrologer, geographer, historian, mathematician, and teacher native to Apamea (Syria), Apame ...
( BC). In this scheme, a quadrilateral can be a parallelogram or a non-parallelogram. A parallelogram can itself be a square, an oblong (non-square rectangle), a rhombus, or a rhomboid (non-rhombus non-rectangle). A non-parallelogram can be a ''trapezium'' with exactly one pair of parallel sides, which can be ''isosceles'' (with equal legs) or ''scalene'' (with unequal legs); or a ''trapezoid'' (τραπεζοειδή, literally "table-like") with no parallel sides.
All European languages except for English follow Proclus's meanings of ''trapezium'' and ''trapezoid'', as did English until the late 18th century, when an influential mathematical dictionary published by Charles Hutton
Charles Hutton FRS FRSE LLD (14 August 1737 – 27 January 1823) was an English mathematician and surveyor. He was professor of mathematics at the Royal Military Academy, Woolwich from 1773 to 1807. He is remembered for his calculation of th ...
in 1795 transposed the two terms without explanation, leading to widespread inconsistency. Hutton's change was reversed in British English in about 1875, but it has been retained in American English to the present. Late 19th century American geometry textbooks define a trapezium as having ''no'' parallel sides, a trapezoid as having ''exactly one'' pair of parallel sides, and a parallelogram as having two sets of opposing parallel sides.
To avoid confusion between contradictory British and American meanings of ''trapezium'' and ''trapezoid'', quadrilaterals with no parallel sides have sometimes been called ''irregular quadrilaterals''.
Special cases
 An
An isosceles trapezoid
In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and bo ...
is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a Reflection (mathematics), reflection. That is, a figure which does not change upon undergoing a reflection has reflecti ...
. This is possible for acute trapezoids or right trapezoids as rectangles. An acute trapezoid is a trapezoid with two adjacent acute angles on its longer base, and the isosceles trapezoid is an example of an acute trapezoid. The isosceles trapezoid has a special case known as a three-sided trapezoid, meaning it is a trapezoid wherein two trapezoid's legs have equal lengths as the trapezoid's base at the top. The isosceles trapezoid is the convex hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, ...
of an antiparallelogram
In geometry, an antiparallelogram is a type of list of self-intersecting polygons, self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general ...
, a type of crossed quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
. Every antiparallelogram is formed with such a trapezoid by replacing two parallel sides by the two diagonals.
An obtuse trapezoid, on the other hand, has one acute and one obtuse angle on each base. An example is parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...
with equal acute angles.
A right trapezoid is a trapezoid with two adjacent right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
. One special type of right trapezoid is by forming three right triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees).
The side opposite to the right angle i ...
s, which was used by James Garfield
James Abram Garfield (November 19, 1831 – September 19, 1881) was the 20th president of the United States, serving from March 1881 until Assassination of James A. Garfield, his death in September that year after being shot two months ea ...
to prove the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
.
A tangential trapezoid is a trapezoid that has an incircle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter ...
.
Condition of existence
Four lengths ''a'', ''c'', ''b'', ''d'' can constitute the consecutive sides of a non-parallelogram trapezoid with ''a'' and ''b'' parallel only when : The quadrilateral is a parallelogram when , but it is an ex-tangential quadrilateral (which is not a trapezoid) when .Characterizations
angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s that are supplementary, that is, they add up to 180 degrees.
*The angle between a side and a diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek � ...
is equal to the angle between the opposite side and the same diagonal.
*The diagonals cut each other in mutually the same ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
(this ratio is the same as that between the lengths of the parallel sides).
*The diagonals cut the quadrilateral into four triangles
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensiona ...
of which one opposite pair have equal areas.
*The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal.
*The areas ''S'' and ''T'' of some two opposite triangles of the four triangles formed by the diagonals satisfy the equation
::
:where ''K'' is the area of the quadrilateral.
*The midpoints of two opposite sides of the trapezoid and the intersection of the diagonals are collinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, t ...
.
*The angles in the quadrilateral ''ABCD'' satisfy
*The cosines of two adjacent angles sum to 0, as do the cosines of the other two angles.
*The cotangents of two adjacent angles sum to 0, as do the cotangents of the other two adjacent angles.
*One bimedian divides the quadrilateral into two quadrilaterals of equal areas.
*Twice the length of the bimedian connecting the midpoints of two opposite sides equals the sum of the lengths of the other sides.
Additionally, the following properties are equivalent, and each implies that opposite sides ''a'' and ''b'' are parallel:
* The consecutive sides ''a'', ''c'', ''b'', ''d'' and the diagonals ''p'', ''q'' satisfy the equation
::
*The distance ''v'' between the midpoints of the diagonals satisfies the equation
::
Properties
Midsegment and height
The ''midsegment'' or ''median'' of a trapezoid is the segment that joins themidpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dim ...
s of the legs. It is parallel to the bases. Its length ''m'' is equal to the average of the lengths of the bases ''a'' and ''b'' of the trapezoid,
:
The midsegment of a trapezoid is one of the two bimedians (the other bimedian divides the trapezoid into equal areas).
The ''height'' (or altitude) is the perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
distance between the bases. In the case that the two bases have different lengths (''a'' ≠ ''b''), the height of a trapezoid ''h'' can be determined by the length of its four sides using the formula
:
where ''c'' and ''d'' are the lengths of the legs and .
Area
The area of a trapezoid is given by the product of the midsegment (the average of the two bases) and the height: where and are the lengths of the bases, and is the height (the perpendicular distance between these sides). This method has been used inAryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
's ''Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Indian astronomy, Sanskrit astronomical treatise, is the ''Masterpiece, magnum opus'' and only known surviving work of the 5th century Indian mathematics, Indian mathematician Aryabhata. Philos ...
'' in section 2.8 in the classical age of Indian, yielding as a special case the well-known formula for the area of a triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
, by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.
The 7th-century Indian mathematician Bhāskara I derived the following formula for the area of a trapezoid with consecutive sides , , , ::
where and are parallel and . This formula can be factored into a more symmetric version
:
When one of the parallel sides has shrunk to a point (say ''a'' = 0), this formula reduces to Heron's formula for the area of a triangle.
Another equivalent formula for the area, which more closely resembles Heron's formula, is
:
where is the semiperimeter of the trapezoid. (This formula is similar to Brahmagupta's formula, but it differs from it, in that a trapezoid might not be cyclic (inscribed in a circle). The formula is also a special case of Bretschneider's formula for a general quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
).
From Bretschneider's formula, it follows that
:
The bimedian connecting the parallel sides bisects the area. More generally, any line drawn through the midpoint of the median parallel to the bases, that intersects the bases, bisects the area. Any triangle connecting the two ends of one leg to the midpoint of the other leg is also half of the area.
Diagonals
The lengths of the diagonals are where is the short base, is the long base, and and are the trapezoid legs. If the trapezoid is divided into four triangles by its diagonals ''AC'' and ''BD'' (as shown on the right), intersecting at ''O'', then the area of is equal to that of , and the product of the areas of and is equal to that of and . The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides. If is the length of theline segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...
parallel to the bases, passing through the intersection of the diagonals, with one endpoint on each leg, then is the harmonic mean
In mathematics, the harmonic mean is a kind of average, one of the Pythagorean means.
It is the most appropriate average for ratios and rate (mathematics), rates such as speeds, and is normally only used for positive arguments.
The harmonic mean ...
of the lengths of the bases:
:
The line that goes through both the intersection point of the extended nonparallel sides and the intersection point of the diagonals, bisects each base.
Other properties
The center of area (center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
for a uniform lamina
Lamina may refer to:
People
* Saa Emerson Lamina, Sierra Leonean politician
* Tamba Lamina, Sierra Leonean politician and diplomat
Science and technology
* Planar lamina, a two-dimensional planar closed surface with mass and density, in mathem ...
) lies along the line segment joining the midpoints of the parallel sides, at a perpendicular distance ''x'' from the longer side ''b'' given by
:
The center of area divides this segment in the ratio (when taken from the short to the long side)
:
If the angle bisectors to angles ''A'' and ''B'' intersect at ''P'', and the angle bisectors to angles ''C'' and ''D'' intersect at ''Q'', thenOwen Byer, Felix Lazebnik and Deirdre Smeltzer
Deirdre Longacher Smeltzer (born 1964) is an American mathematician, mathematics educator, textbook author, and academic administrator. A former professor, dean, and vice president at Eastern Mennonite University, she is Senior Director for Pro ...
, '' Methods for Euclidean Geometry', Mathematical Association of America, 2010, p. 55.
:
Applications
Incalculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, the definite integral
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Int ...
of a function can be numerically approximated as a discrete sum by partitioning the interval of integration into small uniform intervals and approximating the function's value on each interval as the average of the values at its endpoints:
where is the number of intervals, , , and . Graphically, this amounts to approximating the region under the graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
of the function by a collection of trapezoids, so this method is called the '' trapezoidal rule''.
When any rectangle is viewed in perspective from a position which is centered on one axis but not the other, it appears to be an isosceles trapezoid, called the keystone effect because arch keystones are commonly trapezoidal. For example, when a rectangular building façade
A façade or facade (; ) is generally the front part or exterior of a building. It is a loanword from the French language, French (), which means "frontage" or "face".
In architecture, the façade of a building is often the most important asp ...
is photographed from the ground at a position directly in front using a rectilinear lens
In photography, a rectilinear lens is a photographic lens that yields images where straight features, such as the edges of walls of buildings, appear with straight lines, as opposed to being curved. In other words, it is a lens with little or n ...
, the image of the building is an isosceles trapezoid. Such photographs sometimes have a "keystone transformation" applied to them to recover rectangular shapes. Video projector
A video projector is an image projector that receives a video signal and projects the corresponding image onto a projection screen using a lens system. Video projectors use a very bright ultra-high-performance lamp (a special mercury arc l ...
s sometimes apply such a keystone transformation to the recorded image before projection, so that the image projected on a flat screen appears undistorted.
Trapezoidal doors and windows were the standard style for the Inca
The Inca Empire, officially known as the Realm of the Four Parts (, ), was the largest empire in pre-Columbian America. The administrative, political, and military center of the empire was in the city of Cusco. The History of the Incas, Inca ...
, although it can be found used by earlier cultures of the same region and did not necessarily originate with them.
An almena, a battlement
A battlement, in defensive architecture, such as that of city walls or castles, comprises a parapet (a defensive low wall between chest-height and head-height), in which gaps or indentations, which are often rectangular, occur at intervals ...
feature characteristic of Moorish architecture, is trapezoidal.
Michaelangelo's redesign of the Piazza del Campidoglio
Piazza del Campidoglio ("Capitoline Square") is a public square (piazza) on the top of the ancient Capitoline Hill, between the Roman Forum and the Campus Martius in Rome, Italy. The square includes three main buildings, the Palazzo Senatorio (Se ...
(see photograph at right) incorporated a trapezoid surrounding an ellipse, giving the effect of a square surrounding a circle when seen foreshortened at ground level.
Cinematography
Cinematography () is the art of motion picture (and more recently, electronic video camera) photography.
Cinematographers use a lens (optics), lens to focus reflected light from objects into a real image that is transferred to some image sen ...
takes advantage of trapezoids in the opposite way, to produce an excessive foreshortening effect from the camera viewpoint, giving the illusion of greater depth to a room in a movie studio than the set physically has.
Trapezoids were also used to produce the visual distortions of Caligarism.
Canal
Canals or artificial waterways are waterways or engineered channels built for drainage management (e.g. flood control and irrigation) or for conveyancing water transport vehicles (e.g. water taxi). They carry free, calm surface ...
s and drainage ditch
A ditch is a small to moderate trench created to channel water. A ditch can be used for drainage, to drain water from low-lying areas, alongside roadways or fields, or to channel water from a more distant source for plant irrigation. Ditches ...
es commonly have a trapezoidal cross-section.
In biology, especially morphology
Morphology, from the Greek and meaning "study of shape", may refer to:
Disciplines
*Morphology (archaeology), study of the shapes or forms of artifacts
*Morphology (astronomy), study of the shape of astronomical objects such as nebulae, galaxies, ...
and taxonomy
image:Hierarchical clustering diagram.png, 280px, Generalized scheme of taxonomy
Taxonomy is a practice and science concerned with classification or categorization. Typically, there are two parts to it: the development of an underlying scheme o ...
, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
Trapezoids are sometimes used as a graphical symbol. In circuit diagram
A circuit diagram (or: wiring diagram, electrical diagram, elementary diagram, electronic schematic) is a graphical representation of an Electrical network, electrical circuit. A pictorial circuit diagram uses simple images of components, whil ...
s, a trapezoid is the symbol for a multiplexer
In electronics, a multiplexer (or mux; spelled sometimes as multiplexor), also known as a data selector, is a device that selects between several Analog signal, analog or Digital signal (electronics), digital input signals and forwards the sel ...
. An isosceles trapezoid is used for the shape of road signs, for example, on secondary highways in Ontario, Canada
Ontario is the southernmost Provinces and territories of Canada, province of Canada. Located in Central Canada, Ontario is the Population of Canada by province and territory, country's most populous province. As of the 2021 Canadian census, it ...
.
Non-Euclidean geometry
In spherical orhyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
, the internal angles of a quadrilateral do not sum to 360°, but quadrilaterals analogous to trapezoids, parallelograms, and rectangles can still be defined, and additionally there are a few new types of quadrilaterals not distinguished in the Euclidean case.
A spherical or hyperbolic trapezoid is a quadrilateral with two opposite sides, the legs, each of whose two adjacent angles sum to the same quantity; the other two sides are the bases. As in Euclidean geometry, special cases include isosceles trapezoids whose legs are equal (as are the angles adjacent to each base), parallelograms with two pairs of opposite equal angles and two pairs of opposite equal sides, rhombuses with two pairs of opposite equal angles and four equal sides, rectangles with four equal (non-right) angles and two pairs of opposite equal sides, and squares with four equal (non-right) angles and four equal sides.
When a rectangle is cut in half along the line through the midpoints of two opposite sides, each of the resulting two pieces is an isosceles trapezoid with two right angles, called a Saccheri quadrilateral. When a rectangle is cut into quarters by the two lines through pairs of opposite midpoints, each of the resulting four pieces is a quadrilateral with three right angles called a Lambert quadrilateral. In Euclidean geometry Saccheri and Lambert quadrilaterals are merely rectangles.
Related topics
positive integer
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positiv ...
s obtained by summing consecutively two or more positive integers greater than one, forming a trapezoidal pattern.
The crossed ladders problem is the problem of finding the distance between the parallel sides of a right trapezoid, given the diagonal lengths and the distance from the perpendicular leg to the diagonal intersection.
See also
* Frustum, a solid having trapezoidal faces * Wedge, a polyhedron defined by two triangles and three trapezoid faces.Notes
Bibliography
* * * * * * * * *Further reading
*External links
"Trapezium"
at the ''
Encyclopedia of Mathematics
The ''Encyclopedia of Mathematics'' (also ''EOM'' and formerly ''Encyclopaedia of Mathematics'') is a large reference work in mathematics.
Overview
The 2002 version contains more than 8,000 entries covering most areas of mathematics at a graduat ...
''
*
Trapezoid definition
(with interactive animations)
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
' (2008) {{Polygons Elementary shapes Types of quadrilaterals