|
Antiparallelogram
In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, sides in the longer pair cross each other as in a scissors mechanism. Antiparallelograms are also called contraparallelograms or crossed parallelograms. Antiparallelograms occur as the vertex figures of certain nonconvex uniform polyhedra. In the theory of four-bar linkages, the linkages with the form of an antiparallelogram are also called butterfly linkages or bow-tie linkages, and are used in the design of non-circular gears. In celestial mechanics, they occur in certain families of solutions to the 4-body problem. Every antiparallelogram has an axis of symmetry, with all four vertices on a circle. It can be formed from an isosceles trapezoid by adding the two diagonals and removing two parallel sides. The signed area of every antiparallelogram ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
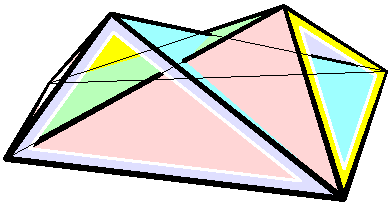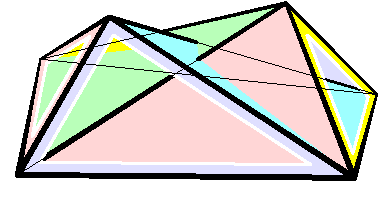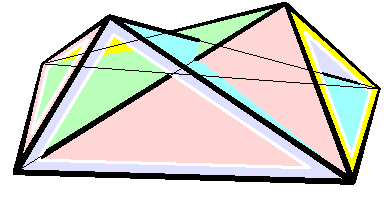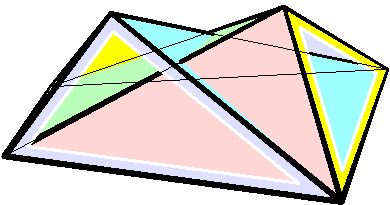
Bricard Octahedron
In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossings requires more vertices (at least nine) than the six vertices of the Bricard octahedra.. In his publication describing these octahedra, Bricard completely classified the flexible octahedra. His work in this area was later the subject of lectures by Henr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Rhombihexacron
In geometry, the small rhombihexacron (or small dipteral disdodecahedron) is the dual of the small rhombihexahedron. It is visually identical to the small hexacronic icositetrahedron. Its faces are antiparallelograms formed by pairs of coplanar triangles. Proportions Each antiparallelogram has two angles of \arccos(\frac+\frac\sqrt)\approx 16.842\,116\,236\,30^ and two angles of \arccos(-\frac+\frac\sqrt)\approx 98.421\,058\,118\,15^. The diagonals of each antiparallelogram intersect at an angle of \arccos(\frac+\frac\sqrt)\approx 64.736\,825\,645\,55^. The dihedral angle A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equals \arccos(\frac)\approx 138.117\,959\,055\,51^. The ratio between the lengths of the long edges and the short ones equals \sqrt. References * External li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Trapezoid
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal length (properties shared with the parallelogram). The diagonals are also of equal length. The base angles of an isosceles trapezoid are equal in measure (there are in fact two pairs of equal base angles, where one base angle is the supplementary angle of a base angle at the other base). Special cases Rectangles and squares are usually considered to be special cases of isosceles trapezoids thou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Self-intersecting Polygons
Self-intersecting polygons, crossed polygons, or self-crossing polygons are polygons some of whose edges cross each other. They contrast with simple polygons, whose edges never cross. Some types of self-intersecting polygons are: *the crossed quadrilateral, with four edges **the antiparallelogram, a crossed quadrilateral with alternate edges of equal length ***the crossed rectangle, an antiparallelogram whose edges are two opposite sides and the two diagonals of a rectangle, hence having two edges parallel *Star polygons **pentagram, with five edges **heptagram, with seven edges **octagram, with eight edges ** enneagram or nonagram, with nine edges **decagram, with ten edges **hendecagram, with eleven edges **dodecagram In geometry, a dodecagram ( Henry George Liddell, Rob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crossed Quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a '' square''. The term " oblong" is occasionally used to refer to a non- square rectangle. A rectangle with vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal. Other geometries, such as spherical, elliptic, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Rhombihexahedron
In geometry, the small rhombihexahedron (or small rhombicube) is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces (12 squares and 6 octagons), 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram. Related polyhedra This polyhedron shares the vertex arrangement with the stellated truncated hexahedron. It additionally shares its edge arrangement with the convex rhombicuboctahedron (having 12 square faces in common) and with the small cubicuboctahedron (having the octagonal faces in common). It may be constructed as the exclusive or (blend) of three octagonal prisms. External links * Polyhedra {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Varignon Parallelogram
Varignon's theorem is a statement in Euclidean geometry, that deals with the construction of a particular parallelogram, the Varignon parallelogram, from an arbitrary quadrilateral (quadrangle). It is named after Pierre Varignon, whose proof was published posthumously in 1731. Theorem The midpoints of the sides of an arbitrary quadrilateral form a parallelogram. If the quadrilateral is convex or concave (not complex), then the area of the parallelogram is half the area of the quadrilateral. If one introduces the concept of oriented areas for ''n''-gons, then this area equality also holds for complex quadrilaterals. Coxeter, H. S. M. and Greitzer, S. L. "Quadrangle; Varignon's theorem" §3.1 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 52–54, 1967. The Varignon parallelogram exists even for a skew quadrilateral, and is planar whether the quadrilateral is planar or not. The theorem can be generalized to the midpoint polygon of an arbitrary polygon. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Quadrilateral
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the ''circumcircle'' or ''circumscribed circle'', and the vertices are said to be '' concyclic''. The center of the circle and its radius are called the ''circumcenter'' and the ''circumradius'' respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case. The word cyclic is from the Ancient Greek (''kuklos''), which means "circle" or "wheel". All triangles have a circumcircle, but not all quadrilaterals do. An example of a quadrilateral that cannot be cyclic is a non-square rhombus. The section characterizations below states wha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |