Spectral Estimation Of Multidimensional Signals

Multidimension spectral estimation is a generalization of spectral estimation, normally formulated for one-dimensional signals, to multidimensional signals or multivariate data, such as wave vectors.

Motivation

Multidimensional spectral estimation has gained popularity because of its application in fields like medicine, aerospace, sonar, radar, bio informatics and geophysics. In the recent past, a number of methods have been suggested to design models with finite parameters to estimate the power spectrum of multidimensional signals. In this article, we will be looking into the basics of methods used to estimate the power spectrum of multidimensional signals.

Applications

There are many applications of spectral estimation of multi-D signals such as classification of signals as low pass, high pass, pass band and stop band. It is also used in compression and coding of audio and video signals, beam forming and direction finding in radars, Seismic data estimation and processing, array of sensors and antennas and vibrational analysis. In the field of radio astronomy, it is used to synchronize the outputs of an array of telescopes.

Basic Concepts

In a single dimensional case, a signal is characterized by an amplitude and a time scale. The basic concepts involved in spectral estimation include autocorrelation, multi-D Fourier transform, mean square error and entropy. When it comes to multidimensional signals, there are two main approaches: use a bank of filters or estimate the parameters of the random process in order to estimate the power spectrum.

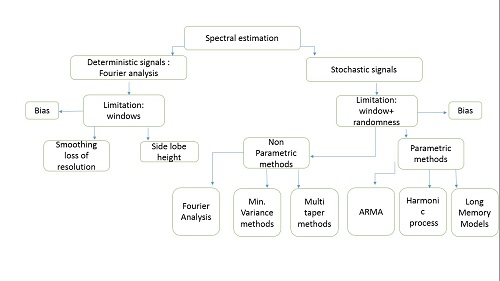
Methods

Classical Estimation Theory

It is a technique to estimate the power spectrum of a single dimensional or a multidimensional signal as it cannot be calculated accurately. Given are samples of a wide sense stationary random process and its second order statistics (measurements).The estimates are obtained by applying a multidimensional Fourier transform of the autocorrelation function of the random signal. The estimation begins by calculating a periodogram which is obtained by squaring the magnitude of the multidimensional Fourier transform of the measurements ri(n). The spectral estimates obtained from the periodogram have a large variance in amplitude for consecutive periodogram samples or in wavenumber. This problem is resolved using techniques that constitute the classical estimation theory. They are as follows:
1.Bartlett suggested a method that averages the spectral estimates to calculate the power spectrum. The measurements are divided into equally spaced segments in time and an average is taken. This gives a better estimate.
2.Based on the wavenumber and index of the receiver/output we can partition the segments. This increases the spectral estimates and decreases the variances between consecutive segments.
3.Welch suggested that we should divide the measurements using data window functions, calculate a periodogram, average them to get a spectral estimate and calculate the power spectrum using Fast Fourier Transform (FFT). This increases the computational speed.
4.Smoothing window will help us smoothen the estimate by multiplying the periodogram with a smoothening spectrum. Wider the main lobe of the smoothening spectrum, smoother it becomes at the cost of frequency resolution.

:$P\left (K_x,w\right)=\int_^\infty \int_^\infty \varphi_\left(x,t\right)\ e^\,dx\,dt$

:\varphi_\left(x,t\right)=s\left left(\xi,\tau\right)s^*\left(\xi-x,\tau-t\right)\right/math>

:$P_B\left(w\right) = \frac\sum_, \sum_\ x\left(n+MI\right)\ e^, ^2$ Bartlett's case

:$P_M\left(w\right) = \frac, \sum_\ g\left(n\right)\ x\left(n\right)\ e^, ^2$ Modified periodogram

:$P_W\left(w\right) = \frac\sum_, \sum_\ g\left(n\right)\ x\left(n+MI\right)\ e^, ^2$ Welch's case

; Advantages
: Straightforward method involving Fourier transforms.

; Limitations
# Since some of the above methods sample the sequence in time, the frequency resolution is reduced (aliasing).
# Number of instances of a wide sense stationary random process are less which makes it difficult to calculate the estimates accurately.

High Resolution Spectral Estimations

This method gives a better estimate whose frequency resolution is higher than the classical estimation theory. In the high resolution estimation method we use a variable wavenumber window which allows only certain wavenumbers and suppresses the others. Capon’s work helped us establish an estimation method by using wavenumber-frequency components. This results in an estimate with a higher frequency resolution. It is similar to maximum likelihood method as the optimization tool used is similar.

; Assumption
: The output obtained from the sensors is a wide sense stationary random process with zero mean.

:P_C\left(K_ox,w_o\right) = E\left

; Advantages
# Higher frequency resolution compare to other existing methods.
# Better frequency estimate since we are using a variable wavenumber window as compared to classical method which uses a fixed wavenumber window.
# Faster Computational speed as it uses FFT.

Separable Spectral Estimator

In this type of estimation, we select the multidimensional signal to be a separable function. Because of this property we will be able to view the Fourier analysis taking place in multiple dimensions successively. A time delay in the magnitude squaring operation will help us process the Fourier transformation in each dimension. A Discrete time Multidimensional Fourier transform is applied along each dimension and in the end a maximum entropy estimator is applied and the magnitude is squared.

; Advantages
# The Fourier analysis is flexible as the signal is separable.
# It preserves the phase components of every dimension unlike other spectral estimators.

All-pole Spectral Modelling

This method is an extension of a 1-D technique called Autoregressive spectral estimation. In autoregressive models, the output variables depend linearly on its own previous values. In this model, the estimation of power spectrum is reduced to estimating the coefficients from the autocorrelation coefficients of the random process which are assumed to be known for a specific region. The power spectrum $P_A(k_x,w)$ of a random process $r(i,n)$ is given by:

:$P_A\left(k_x,w\right) = P_e\left(k_x,w\right), \frac, ^2$

Above, $P_e\left(k_x,w\right)$ is the power spectrum of a random process $e(i,n)$ , which is given as the input to a system with a transfer function $, \frac,$ to obtain $r(i,n)$ and $A\left(k_x,w\right)$ is:

:$A\left(k_x,w\right) = \sum_^\sum_^a(p,q)exp(jk_xp - jwq)$

Therefore, the power estimation reduces to estimation of coefficients of $a\left(p, q\right)$ from the auto correlation function $\varphi\left(l,m\right)$of the random process. The coefficients can also be estimated using the linear prediction formulation which deals with minimization of mean square error between the actual random signal and predicted values of the random signal.

;Limitations
# In 1-D we have the same number of linear equations with the same number of unknowns because of the autocorrelation matching property. But it may not be possible in multi-D since the set of parameters does not contain enough degrees of freedom to match autocorrelation coefficients.
# We assume that the array of coefficients is limited to a certain area.
# In 1-D formulation of linear prediction, the inverse filter has minimum phase property thus proving that the filter is stable. It is not always necessarily true in multi-D case.
# In 1-D formulation, the autocorrelation matrix is positive definite but positive definite extension may not exist in the case of multi-D.

Maximum Entropy Spectral Estimation

In this method of spectral estimation, we try to find the spectral estimate whose inverse Fourier transform matches the known auto correlation coefficients. We maximize the entropy of the spectral estimate such that it matches the autocorrelation coefficients.Dan E. Dudgeon, Russell M. Mersereau, “Multidimensional Digital Signal Processing”, Prentice-Hall Signal Processing Series, ,pp. 315-338, 1983. The entropy equation is given as:

:$H = \frac \int_^ \int_^ log P\left(k_x,w\right)dk_xdw$

The power spectrum $P\left(k,w\right)$ can be expressed as a sum of known autocorrelation coefficients and unknown autocorrelation coefficients. By adjusting the values of unconstrained coefficients, the entropy can be maximized.

The max entropy is of the form:

:$P_ = \frac$

λ(l,m) must be chosen such that known autocorrelation coefficients are matched.

;Limitations
# It has constrained optimization. It can be overcome by using the method of Lagrange multipliers.
# All pole spectral estimate is not the solution to maximum entropy in multidimensional case as it is in the case of 1-D. This is because the all pole spectral model does not contain enough degree of freedom to match the know autocorrelation coefficients.

; Advantages
: Errors in measuring or estimating the known autocorrelation coefficients can be taken into account since exact match is not required.
; Disadvantage
: Too many computations are required.

Improved Maximum Likelihood Method(IMLM)

This is a relatively new approach. Improved maximum likelihood method (IMLM) is a combination of two MLM(maximum likelihood) estimators. The improved maximum likelihood of two 2-dimensional arrays A and B at a wave number k( gives information about the orientation of the array in space) is given by the relation:

:$IMLM\left(k :A,B\right)=\frac$

Array B is a subset of A. Therefore, assuming that A>B, if there is a difference between the MLM of A and MLM of B then significant part of the estimated spectral energy at the frequency may be due to power leakage from other frequencies. The de-emphasis of MLM of A may improve spectral estimate. This is accomplished by multiplying by a weighted function which is smaller when there is a greater difference between MLA of B and MLA of A.

:$IMLM\left(k :A,B\right)=\frac$
:$IMLM\left(k :A,B\right)= MLM\left(k :A\right) W_\left(k\right)$

where $W_\left(k\right)$ is the weighting function and is given by the expression:

:$W_\left(k\right)= \frac$

; Advantages
# Used as an alternative to MLM or MEM(Maximum Entropy Method/principle of maximum entropy)
# IMLM has better resolution than MLM and it requires lesser number of computations when compared to MEM

References

{{Reflist

Digital signal processing
Multidimensional signal processing>y\left(i,n\right), ^2\right= \frac

; Advantages
# Higher frequency resolution compare to other existing methods.
# Better frequency estimate since we are using a variable wavenumber window as compared to classical method which uses a fixed wavenumber window.
# Faster Computational speed as it uses FFT.

Separable Spectral Estimator

In this type of estimation, we select the multidimensional signal to be a separable function. Because of this property we will be able to view the Fourier analysis taking place in multiple dimensions successively. A time delay in the magnitude squaring operation will help us process the Fourier transformation in each dimension. A Discrete time Multidimensional Fourier transform is applied along each dimension and in the end a maximum entropy estimator is applied and the magnitude is squared.

; Advantages
# The Fourier analysis is flexible as the signal is separable.
# It preserves the phase components of every dimension unlike other spectral estimators.

All-pole Spectral Modelling

This method is an extension of a 1-D technique called Autoregressive spectral estimation. In autoregressive models, the output variables depend linearly on its own previous values. In this model, the estimation of power spectrum is reduced to estimating the coefficients from the autocorrelation coefficients of the random process which are assumed to be known for a specific region. The power spectrum $P_A(k_x,w)$ of a random process $r(i,n)$ is given by:

:$P_A\left(k_x,w\right) = P_e\left(k_x,w\right), \frac, ^2$

Above, $P_e\left(k_x,w\right)$ is the power spectrum of a random process $e(i,n)$ , which is given as the input to a system with a transfer function $, \frac,$ to obtain $r(i,n)$ and $A\left(k_x,w\right)$ is:

:$A\left(k_x,w\right) = \sum_^\sum_^a(p,q)exp(jk_xp - jwq)$

Therefore, the power estimation reduces to estimation of coefficients of $a\left(p, q\right)$ from the auto correlation function $\varphi\left(l,m\right)$of the random process. The coefficients can also be estimated using the linear prediction formulation which deals with minimization of mean square error between the actual random signal and predicted values of the random signal.

;Limitations
# In 1-D we have the same number of linear equations with the same number of unknowns because of the autocorrelation matching property. But it may not be possible in multi-D since the set of parameters does not contain enough degrees of freedom to match autocorrelation coefficients.
# We assume that the array of coefficients is limited to a certain area.
# In 1-D formulation of linear prediction, the inverse filter has minimum phase property thus proving that the filter is stable. It is not always necessarily true in multi-D case.
# In 1-D formulation, the autocorrelation matrix is positive definite but positive definite extension may not exist in the case of multi-D.

Maximum Entropy Spectral Estimation

In this method of spectral estimation, we try to find the spectral estimate whose inverse Fourier transform matches the known auto correlation coefficients. We maximize the entropy of the spectral estimate such that it matches the autocorrelation coefficients.Dan E. Dudgeon, Russell M. Mersereau, “Multidimensional Digital Signal Processing”, Prentice-Hall Signal Processing Series, ,pp. 315-338, 1983. The entropy equation is given as:

:$H = \frac \int_^ \int_^ log P\left(k_x,w\right)dk_xdw$

The power spectrum $P\left(k,w\right)$ can be expressed as a sum of known autocorrelation coefficients and unknown autocorrelation coefficients. By adjusting the values of unconstrained coefficients, the entropy can be maximized.

The max entropy is of the form:

:$P_ = \frac$

λ(l,m) must be chosen such that known autocorrelation coefficients are matched.

;Limitations
# It has constrained optimization. It can be overcome by using the method of Lagrange multipliers.
# All pole spectral estimate is not the solution to maximum entropy in multidimensional case as it is in the case of 1-D. This is because the all pole spectral model does not contain enough degree of freedom to match the know autocorrelation coefficients.

; Advantages
: Errors in measuring or estimating the known autocorrelation coefficients can be taken into account since exact match is not required.
; Disadvantage
: Too many computations are required.

Improved Maximum Likelihood Method(IMLM)

This is a relatively new approach. Improved maximum likelihood method (IMLM) is a combination of two MLM(maximum likelihood) estimators. The improved maximum likelihood of two 2-dimensional arrays A and B at a wave number k( gives information about the orientation of the array in space) is given by the relation:

:$IMLM\left(k :A,B\right)=\frac$

Array B is a subset of A. Therefore, assuming that A>B, if there is a difference between the MLM of A and MLM of B then significant part of the estimated spectral energy at the frequency may be due to power leakage from other frequencies. The de-emphasis of MLM of A may improve spectral estimate. This is accomplished by multiplying by a weighted function which is smaller when there is a greater difference between MLA of B and MLA of A.

:$IMLM\left(k :A,B\right)=\frac$
:$IMLM\left(k :A,B\right)= MLM\left(k :A\right) W_\left(k\right)$

where $W_\left(k\right)$ is the weighting function and is given by the expression:

:$W_\left(k\right)= \frac$

; Advantages
# Used as an alternative to MLM or MEM(Maximum Entropy Method/principle of maximum entropy)
# IMLM has better resolution than MLM and it requires lesser number of computations when compared to MEM

References

{{Reflist

Digital signal processing
Multidimensional signal processing