self-tiling tile set on:
[Wikipedia]
[Google]
[Amazon]
 A self-tiling tile set, or ''setiset'', of order ''n'' is a set of ''n'' shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of ''n'' shapes. That is, the ''n'' shapes can be assembled in ''n'' different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for ''n'' = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by
A self-tiling tile set, or ''setiset'', of order ''n'' is a set of ''n'' shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of ''n'' shapes. That is, the ''n'' shapes can be assembled in ''n'' different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for ''n'' = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by
/ref> but the problem of finding such sets for ''n'' = 4 was asked decades previously by C. Dudley Langford, and examples for
 From the above definition it follows that a setiset composed of ''n'' identical pieces is the same thing as a 'self-replicating tile' or rep-tile, of which setisets are therefore a generalization. Setisets using ''n'' distinct shapes, such as Figure 1, are called ''perfect''. Figure 2 shows an example for ''n'' = 4 which is ''imperfect'' because two of the component shapes are the same.
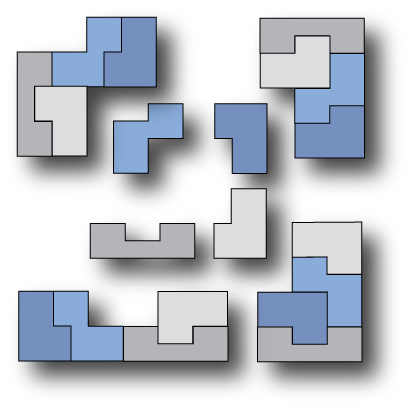
The shapes employed in a setiset need not be ''connected'' regions. Disjoint pieces composed of two or more separated islands are also permitted. Such pieces are described as ''disconnected'', or ''weakly-connected'' (when islands join only at a point), as seen in the setiset shown in Figure 3.
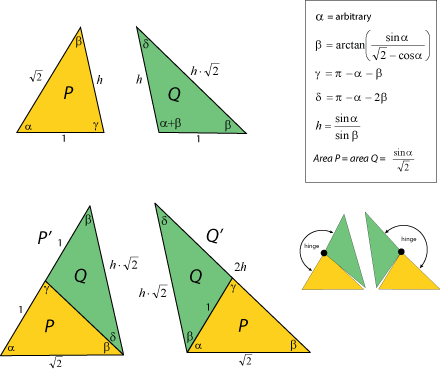
The fewest pieces in a setiset is two. Figure 4 encapsulates an infinite family of order 2 setisets each composed of two triangles, ''P'' and ''Q''. As shown, the latter can be hinged together to produce a compound triangle that has the same shape as ''P'' or ''Q'', depending upon whether the hinge is fully open or fully closed. This unusual specimen thus provides an example of a hinged dissection.
From the above definition it follows that a setiset composed of ''n'' identical pieces is the same thing as a 'self-replicating tile' or rep-tile, of which setisets are therefore a generalization. Setisets using ''n'' distinct shapes, such as Figure 1, are called ''perfect''. Figure 2 shows an example for ''n'' = 4 which is ''imperfect'' because two of the component shapes are the same.
The shapes employed in a setiset need not be ''connected'' regions. Disjoint pieces composed of two or more separated islands are also permitted. Such pieces are described as ''disconnected'', or ''weakly-connected'' (when islands join only at a point), as seen in the setiset shown in Figure 3.
The fewest pieces in a setiset is two. Figure 4 encapsulates an infinite family of order 2 setisets each composed of two triangles, ''P'' and ''Q''. As shown, the latter can be hinged together to produce a compound triangle that has the same shape as ''P'' or ''Q'', depending upon whether the hinge is fully open or fully closed. This unusual specimen thus provides an example of a hinged dissection.

 The properties of setisets mean that their pieces form substitution tilings, or
The properties of setisets mean that their pieces form substitution tilings, or
 Besides self-tiling tile sets, which can be interpreted as loops of length 1, there exist longer loops, or closed chains of sets, in which every set tiles its successor.''Geometric Hidden Gems'' by Jean-Paul Delahaye in Scilogs
Besides self-tiling tile sets, which can be interpreted as loops of length 1, there exist longer loops, or closed chains of sets, in which every set tiles its successor.''Geometric Hidden Gems'' by Jean-Paul Delahaye in Scilogs
April 07, 2013 Figure 6 shows a pair of mutually tiling sets of decominoes, in other words, a loop of length 2. Sallows and Schotel did an exhaustive search of order 4 sets that are composed of octominoes. In addition to seven ordinary setisets (i.e., loops of length 1) they found a bewildering variety of loops of every length up to a maximum of 14. The total number of loops identified was nearly one and a half million. More research in this area remains to be done, but it seems safe to suppose that other shapes may also entail loops.Self-Tiling Tile Sets website
/ref>


Self-Tiling Tile Sets website
{{Tessellation Tessellation Self-replication
 A self-tiling tile set, or ''setiset'', of order ''n'' is a set of ''n'' shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of ''n'' shapes. That is, the ''n'' shapes can be assembled in ''n'' different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for ''n'' = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by
A self-tiling tile set, or ''setiset'', of order ''n'' is a set of ''n'' shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of ''n'' shapes. That is, the ''n'' shapes can be assembled in ''n'' different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for ''n'' = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by Lee Sallows
Lee Cecil Fletcher Sallows (born April 30, 1944) is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares. ...
in 2012,Alejandro Erickson on Self-tiling tile sets/ref> but the problem of finding such sets for ''n'' = 4 was asked decades previously by C. Dudley Langford, and examples for
polyabolo
In recreational mathematics, a polyabolo (also known as a polytan) is a shape formed by gluing isosceles right triangles edge-to-edge, making a polyform with the isosceles right triangle as the base form. Polyaboloes were introduced by Martin Gar ...
es (discovered by Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of L ...
, Wade E. Philpott and others) and polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
Polyominoes have been used in po ...
es (discovered by Maurice J. Povah) were previously published by Gardner.''Polyhexes and Polyaboloes'' in ''Mathematical Magic Show'', by Martin Gardner, Knopf, 1977, pp 146-159
Examples and definitions
 From the above definition it follows that a setiset composed of ''n'' identical pieces is the same thing as a 'self-replicating tile' or rep-tile, of which setisets are therefore a generalization. Setisets using ''n'' distinct shapes, such as Figure 1, are called ''perfect''. Figure 2 shows an example for ''n'' = 4 which is ''imperfect'' because two of the component shapes are the same.
The shapes employed in a setiset need not be ''connected'' regions. Disjoint pieces composed of two or more separated islands are also permitted. Such pieces are described as ''disconnected'', or ''weakly-connected'' (when islands join only at a point), as seen in the setiset shown in Figure 3.
The fewest pieces in a setiset is two. Figure 4 encapsulates an infinite family of order 2 setisets each composed of two triangles, ''P'' and ''Q''. As shown, the latter can be hinged together to produce a compound triangle that has the same shape as ''P'' or ''Q'', depending upon whether the hinge is fully open or fully closed. This unusual specimen thus provides an example of a hinged dissection.
From the above definition it follows that a setiset composed of ''n'' identical pieces is the same thing as a 'self-replicating tile' or rep-tile, of which setisets are therefore a generalization. Setisets using ''n'' distinct shapes, such as Figure 1, are called ''perfect''. Figure 2 shows an example for ''n'' = 4 which is ''imperfect'' because two of the component shapes are the same.
The shapes employed in a setiset need not be ''connected'' regions. Disjoint pieces composed of two or more separated islands are also permitted. Such pieces are described as ''disconnected'', or ''weakly-connected'' (when islands join only at a point), as seen in the setiset shown in Figure 3.
The fewest pieces in a setiset is two. Figure 4 encapsulates an infinite family of order 2 setisets each composed of two triangles, ''P'' and ''Q''. As shown, the latter can be hinged together to produce a compound triangle that has the same shape as ''P'' or ''Q'', depending upon whether the hinge is fully open or fully closed. This unusual specimen thus provides an example of a hinged dissection.


Inflation and deflation
 The properties of setisets mean that their pieces form substitution tilings, or
The properties of setisets mean that their pieces form substitution tilings, or tessellations
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of ge ...
in which the prototiles can be dissected or combined so as to yield smaller or larger duplicates of themselves. Clearly, the twin actions of forming still larger and larger copies (known as inflation), or still smaller and smaller dissections (deflation), can be repeated indefinitely. In this way, setisets can produce non-periodic tilings. However, none of the non-periodic tilings thus far discovered qualify as aperiodic
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
, because the prototiles can always be rearranged so as to yield a periodic tiling. Figure 5 shows the first two stages of inflation of an order 4 set leading to a non-periodic tiling.
Loops
 Besides self-tiling tile sets, which can be interpreted as loops of length 1, there exist longer loops, or closed chains of sets, in which every set tiles its successor.''Geometric Hidden Gems'' by Jean-Paul Delahaye in Scilogs
Besides self-tiling tile sets, which can be interpreted as loops of length 1, there exist longer loops, or closed chains of sets, in which every set tiles its successor.''Geometric Hidden Gems'' by Jean-Paul Delahaye in ScilogsApril 07, 2013 Figure 6 shows a pair of mutually tiling sets of decominoes, in other words, a loop of length 2. Sallows and Schotel did an exhaustive search of order 4 sets that are composed of octominoes. In addition to seven ordinary setisets (i.e., loops of length 1) they found a bewildering variety of loops of every length up to a maximum of 14. The total number of loops identified was nearly one and a half million. More research in this area remains to be done, but it seems safe to suppose that other shapes may also entail loops.
/ref>
Methods of construction
To date, two methods have been used for producing setisets. In the case of sets composed of shapes such aspolyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
Polyominoes have been used in po ...
es, which entail integral piece sizes, a brute force search by computer is possible, so long as ''n'', the number of pieces involved, is not prohibitive. It is easily shown that ''n'' must then be a perfect square
''Perfect Square'' is a 2004 concert film of the alternative rock Musical ensemble, band R.E.M. (band), R.E.M., filmed on July 19, 2003, at the bowling green, Bowling Green in Wiesbaden, Germany. It was released by Warner Reprise Video on March 9, ...
. Figures 1,2,3,5 and 6 are all examples found by this method.
Alternatively, there exists a method whereby multiple copies of a rep-tile can be dissected in certain ways so as to yield shapes that create setisets. Figures 7 and 8 show setisets produced by this means, in which each piece is the union of 2 and 3 rep-tiles, respectively. In Figure 8 can be seen how the 9 pieces above together tile the 3 rep-tile shapes below, while each of the 9 pieces is itself formed by the union of 3 such rep-tile shapes. Hence each shape can be tiled with smaller duplicates of the entire set of 9.


References
External links
Self-Tiling Tile Sets website
{{Tessellation Tessellation Self-replication