|
Lee Sallows
Lee Cecil Fletcher Sallows (born April 30, 1944) is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares. Recreational mathematics Sallows is an expert on the theory of magic squares and has invented several variations on them, including alphamagic squares and geomagic squares. The latter invention caught the attention of mathematician Peter Cameron (mathematician), Peter Cameron who has said that he believes that "an even deeper structure may lie hidden beyond geomagic squares" In "The lost theorem" published in 1997 he showed that every 3 × 3 magic square is associated with a unique parallelogram on the complex plane, a discovery that had escaped all previous researchers from ancient times down to the present day. A golygon is a polygon containing only right angles, such that adjacent sides exhibit consecutive integer lengt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recreational Mathematics
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research-and-application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults and inspiring their further study of the subject. The Mathematical Association of America (MAA) includes recreational mathematics as one of its seventeen Special Interest Groups, commenting: Mathematical competitions (such as those sponsored by mathematical associations) are also categorized under recreational mathematics. Topics Some of the more well-known topics in recreational mathematics are Rubik's Cubes, magic squares, fractals, logic puzzles and mathematical chess problems, but this area of mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
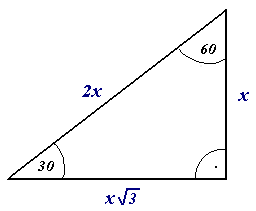
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
London Borough Of Islington
The London Borough of Islington ( ) is a London borough, borough in North London, England. Forming part of Inner London, Islington has an estimated population of 215,667. It was formed in 1965, under the London Government Act 1963, by the amalgamation of the Metropolitan boroughs of the County of London, metropolitan boroughs of Metropolitan Borough of Islington, Islington and Metropolitan Borough of Finsbury, Finsbury. The new entity remains the List of English districts by area, second smallest borough in London and the third-smallest Districts of England, district in England. The borough contains two Westminster United Kingdom Parliament constituencies, parliamentary constituencies; Islington North, represented by former Labour Party (UK), Labour Party leader Jeremy Corbyn, and Islington South & Finsbury represented by Labour Member of Parliament (United Kingdom), MP Emily Thornberry. The local authority is Islington Council. The borough is home to Association football, footb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dame Alice Owen's School
Dame Alice Owen's School (DAOS, or simply Dame Alice Owen's or Owen's) is an 11–18 co-educational, partially selective secondary school and sixth form with academy status in Potters Bar, Hertfordshire, England. It is part of the Dame Alice Owen's Foundation; its trustees are the Worshipful Company of Brewers. It was founded in Islington as a boys' school for 30 students in 1613, which makes it one of the oldest schools in the United Kingdom, and is named after its founder, the 17th-century philanthropist Alice Owen. Over time, the boys' school expanded. A girls' school was built in 1886, and the two schools were merged in 1973; the mixed school moved to its current location at Dugdale Hill Lane in Potters Bar in stages between 1973 and 1976. The school is one of the highest performing state schools in England and Wales in terms of the General Certificate of Secondary Education (GCSE) and GCE Advanced Level (A-Level) results, and is considered one of the best schools i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper Clapton
Clapton is a district of east London, England, in the London Borough of Hackney. Clapton is divided into Upper Clapton, in the north, and Lower Clapton to the south. Clapton railway station lies north-east of Charing Cross. Geography and origins The hamlet of Clapton emerged in the manor and Civil Parish#Ancient Parishes, Ancient Parish of Hackney, London, Hackney. Origins The hamlet of Clapton was, from 1339 (when first recorded) until the 18th century normally rendered as Clopton, meaning the "farm on the hill". The Old English ''clop'' - "lump" or "hill" - presumably denoted the high ground which rises from the River Lea. Clapton grew up as a linear hamlet along the road subsequently known as Lower and Upper Clapton Road. As the area became urbanised, the extent of the area called Clapton eventually increased to encompass most of the north-eastern quarter of Hackney. Scope Because Clapton has never been an administrative unit, it has never had any defined boundaries, thoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hertfordshire
Hertfordshire ( or ; often abbreviated Herts) is a ceremonial county in the East of England and one of the home counties. It borders Bedfordshire to the north-west, Cambridgeshire to the north-east, Essex to the east, Greater London to the south and Buckinghamshire to the west. The largest settlement is Watford, and the county town is Hertford. The county has an area of and had a population of 1,198,800 at the 2021 census. After Watford (131,325), the largest settlements are Hemel Hempstead (95,985), Stevenage (94,470) and the city of St Albans (75,540). For local government purposes Hertfordshire is a non-metropolitan county with ten districts beneath Hertfordshire County Council. Elevations are higher in the north and west, reaching more than in the Chilterns near Tring. The county centres on the headwaters and upper valleys of the rivers Lea and the Colne; both flow south and each is accompanied by a canal. Hertfordshire's undeveloped land is mainly agricultural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brocket Hall
Brocket Hall is a Neoclassical architecture, neo-classical English country house, country house set in a large park at the western side of the urban area of Welwyn Garden City in Hertfordshire, England. The estate is equipped with two golf courses and seven smaller listed buildings, apart from the main house. The freehold on the estate is held by Charles Nall-Cain, 3rd Baron Brocket, the 3rd Baron Brocket. The house is listed building, Grade I-listed. History On the parkland site were two predecessors: the first of these was built in 1239 as Watership or Durantshide Manor, and was early held variously of Hatfield Manor and the Bishop of Ely. A second predecessor was built about 1430: whereas in 1413 John Mortimer had held Waterships, it is known that in 1477 Thomas Brockett held both manors. The house was acquired by John Brocket (died 1558), John Brocket in the early 1550s, and passed to his son John Brocket (died 1598), Sir John Brocket (captain of the personal guard of Elizab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Magazine
''Mathematics Magazine'' is a refereed bimonthly publication of the Mathematical Association of America. Its intended audience is teachers of collegiate mathematics, especially at the junior/senior level, and their students. It is explicitly a journal of mathematics rather than pedagogy. Rather than articles in the terse "theorem-proof" style of research journals, it seeks articles which provide a context for the mathematics they deliver, with examples, applications, illustrations, and historical background. Paid circulation in 2008 was 9,500 and total circulation was 10,000. ''Mathematics Magazine'' is a continuation of ''Mathematics News Letter'' (1926–1934) and ''National Mathematics Magazine'' (1934–1945). Doris Schattschneider became the first female editor of ''Mathematics Magazine'' in 1981. .. The MAA gives the Carl B. Allendoerfer Awards annually "for articles of expository excellence" published in ''Mathematics Magazine''. See also *''American Mathematical Mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (geometry), scaling (enlarging or reducing), possibly with additional translation (geometry), translation, rotation (mathematics), rotation and reflection (mathematics), reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruence (geometry), congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median (geometry)
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect at the triangle's centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. The concept of a median extends to tetrahedra. Relation to center of mass Each median of a triangle passes through the triangle's centroid, which is the center of mass of an infinitely thin object of uniform density coinciding with the triangle. Thus, the object would balance at the intersection point of the medians. The centroid is twice as close along any median to the side that the median intersects as it is to the vertex it emanates from. Equal-area division Each median divides the area of the triangle in half, hence the name, and hence a triangular object of uniform density would balance on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sallows Triangle Theorem
Sallows is a fell in the English Lake District, rising between the valleys of Kentmere and Troutbeck. It is the highest point in the upland area to the south of Garburn Pass, variously termed Kentmere Park and Applethwaite Common on Ordnance Survey maps. Topography Sallows and its sister fell Sour Howes together form a horse-shoe shaped mass, with the opening to the south east. This is the catchment of Park Beck, a tributary of the River Kent. Sallows lies to the north of the beck and connects around the head of the little valley via the ridge of Moor Head. The southern flank of Sallows, above Park Beck, is smooth and grassy, other than for the remains of a quarry. The access track to these workings is still in existence, providing the easiest access from the east. The eastern end of Sallows falls in long easy slopes for half a mile toward the Kent valley, although there are a couple of low crags, particularly on Scour Rigg. The high ground then turns southerly at the subsid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rep-tiles
In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of ''Scientific American''. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in ''Mathematics Magazine''. Terminology A rep-tile is labelled rep-''n'' if the dissection uses ''n'' copies. Such a shape necessarily forms the prototile for a tiling of the plane, in many cases an aperiodic tiling. A rep-tile dissection using different sizes of the original shape is called an irregular rep-tile or irreptile. If the dissection uses ''n'' copies, the shape is said to be irrep-''n''. If all these sub-tiles are of different sizes then the tiling is additionally described as perfect. A shape that is rep-''n'' or irrep-''n'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |