scalenohedron on:
[Wikipedia]
[Google]
[Amazon]
In geometry, a bipyramid, dipyramid, or double pyramid is a
 The symmetric regular right bipyramids have
The symmetric regular right bipyramids have
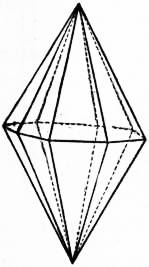 An isotoxal right (symmetric) di--gonal bipyramid is a right (symmetric) -gonal bipyramid with an ''isotoxal'' flat polygon base: its basal vertices are coplanar, but alternate in two radii.
All its faces are
An isotoxal right (symmetric) di--gonal bipyramid is a right (symmetric) -gonal bipyramid with an ''isotoxal'' flat polygon base: its basal vertices are coplanar, but alternate in two radii.
All its faces are
 A generalized -dimensional "bipyramid" is any -
A generalized -dimensional "bipyramid" is any -
The Uniform Polyhedra
The Encyclopedia of Polyhedra ** VRML model
(George Hart)<3><4><5><6><7><8><9><10>
*
Try: "dP''n''", where ''n'' = 3, 4, 5, 6, ... Example: "dP4" is an octahedron. {{Polyhedron navigator Polyhedra
polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
formed by fusing two pyramids
A pyramid () is a Nonbuilding structure, structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a Pyramid (geometry), pyramid in the geometric sense. The base of a pyramid ca ...
together base-to-base. The polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
al base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
and a bipyramid is usually ''symmetric'', meaning the two pyramids are mirror image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it r ...
s across their common base plane. When each apex
The apex is the highest point of something. The word may also refer to:
Arts and media Fictional entities
* Apex (comics)
A-Bomb
Abomination
Absorbing Man
Abraxas
Abyss
Abyss is the name of two characters appearing in Ameri ...
(, the off-base vertices) of the bipyramid is on a line perpendicular to the base and passing through its center, it is a ''right'' bipyramid; otherwise it is ''oblique''. When the base is a regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
, the bipyramid is also called ''regular''.
Definition and properties
A bipyramid is a polyhedron constructed by fusing twopyramids
A pyramid () is a Nonbuilding structure, structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a Pyramid (geometry), pyramid in the geometric sense. The base of a pyramid ca ...
which share the same polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
al base; a pyramid is in turn constructed by connecting each vertex of its base to a single new vertex (the apex
The apex is the highest point of something. The word may also refer to:
Arts and media Fictional entities
* Apex (comics)
A-Bomb
Abomination
Absorbing Man
Abraxas
Abyss
Abyss is the name of two characters appearing in Ameri ...
) not lying in the plane of the base, for an gonal base forming triangular faces in addition to the base face. An gonal bipyramid thus has faces, edges, and vertices. More generally, a right pyramid is a pyramid where the apices are on the perpendicular line through the centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-d ...
of an arbitrary polygon or the incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bis ...
of a tangential polygon
In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle (also called an ''incircle''). This is a circle that is tangent to each of the polygon's sides. The dual po ...
, depending on the source. Likewise, a ''right bipyramid'' is a polyhedron constructed by attaching two symmetrical right bipyramid bases; bipyramids whose apices are not on this line are called ''oblique bipyramids''.
When the two pyramids are mirror images, the bipyramid is called ''symmetric''. It is called ''regular'' if its base is a regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
. When the base is a regular polygon and the apices are on the perpendicular line through its center (a ''regular right bipyramid'') then all of its faces are isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
s; sometimes the name ''bipyramid'' refers specifically to symmetric regular right bipyramids, Examples of such bipyramids are the triangular bipyramid, octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
(square bipyramid) and pentagonal bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an ...
. If all their edges are equal in length, these shapes consist of equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
faces, making them deltahedra
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter Delta (letter), delta resembling a triangular shape Δ.
Deltahedra can be categorized by the prope ...
; the triangular bipyramid and the pentagonal bipyramid are Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s, and the regular octahedron is a Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
.
prismatic symmetry
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2).
Types
Ther ...
, with dihedral symmetry group of order : they are unchanged when rotated of a turn around the axis of symmetry
An axis (: axes) may refer to:
Mathematics
*A specific line (often a directed line) that plays an important role in some contexts. In particular:
** Coordinate axis of a coordinate system
*** ''x''-axis, ''y''-axis, ''z''-axis, common names f ...
, reflected across any plane passing through both apices and a base vertex or both apices and the center of a base edge, or reflected across the mirror plane. Because their faces are transitive under these symmetry transformations, they are isohedral. They are the dual polyhedra of prisms and the prisms are the dual of bipyramids as well; the bipyramids vertices correspond to the faces of the prism, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other, and vice versa. The prisms share the same symmetry as the bipyramids. The regular octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyh ...
is more symmetric still, as its base vertices and apices are indistinguishable and can be exchanged by reflections or rotations; the regular octahedron and its dual, the cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
, have octahedral symmetry
A regular octahedron has 24 rotational (or orientation-preserving) symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedr ...
.
The volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
of a symmetric bipyramid is
where is the area of the base and the perpendicular distance from the base plane to either apex. In the case of a regular sided polygon with side length and whose altitude is , the volume of such a bipyramid is:
Related and other types of bipyramid
Concave bipyramids
A ''concave bipyramid'' has aconcave polygon
A simple polygon that is not convex is called concave, non-convex or reentrant. A concave polygon will always have at least one reflex interior angle—that is, an angle with a measure that is between 180° degrees and 360° degrees exclusive.
...
base, and one example is a concave tetragonal bipyramid or an irregular concave octahedron. A bipyramid with an arbitrary polygonal base could be considered a ''right'' bipyramid if the apices are on a line perpendicular to the base passing through the base's centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-d ...
.
Asymmetric bipyramids
An ''asymmetric bipyramid'' has apices which are not mirrored across the base plane; for a right bipyramid this only happens if each apex is a different distance from the base. The dual of an asymmetric right -gonal bipyramid is an -gonalfrustum
In geometry, a ; (: frusta or frustums) is the portion of a polyhedron, solid (normally a pyramid (geometry), pyramid or a cone (geometry), cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces a ...
.
A regular asymmetric right -gonal bipyramid has symmetry group , of order .
Scalene triangle bipyramids
 An isotoxal right (symmetric) di--gonal bipyramid is a right (symmetric) -gonal bipyramid with an ''isotoxal'' flat polygon base: its basal vertices are coplanar, but alternate in two radii.
All its faces are
An isotoxal right (symmetric) di--gonal bipyramid is a right (symmetric) -gonal bipyramid with an ''isotoxal'' flat polygon base: its basal vertices are coplanar, but alternate in two radii.
All its faces are congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
scalene triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional ...
s, and it is isohedral. It can be seen as another type of a right symmetric di--gonal ''scalenohedron'', with an isotoxal flat polygon base.
An isotoxal right (symmetric) di--gonal bipyramid has two-fold rotation axes through opposite basal vertices, reflection planes through opposite apical edges, an -fold rotation axis through apices, a reflection plane through base, and an -fold rotation-reflection axis through apices, representing symmetry group of order . (The reflection about the base plane corresponds to the rotation-reflection. If is even, then there is an inversion symmetry about the center, corresponding to the rotation-reflection.)
Example with :
:An isotoxal right (symmetric) ditrigonal bipyramid has three similar vertical planes of symmetry, intersecting in a (vertical) -fold rotation axis; perpendicular to them is a fourth plane of symmetry (horizontal); at the intersection of the three vertical planes with the horizontal plane are three similar (horizontal) -fold rotation axes; there is no center of inversion symmetry, but there is a center of symmetry: the intersection point of the four axes.
Example with :
:An isotoxal right (symmetric) ditetragonal bipyramid has four vertical planes of symmetry of two kinds, intersecting in a (vertical) -fold rotation axis; perpendicular to them is a fifth plane of symmetry (horizontal); at the intersection of the four vertical planes with the horizontal plane are four (horizontal) -fold rotation axes of two kinds, each perpendicular to a plane of symmetry; two vertical planes bisect the angles between two horizontal axes; and there is a centre of inversion symmetry.
Double example:
*The bipyramid with isotoxal -gon base vertices and right symmetric apices has its faces isosceles. Indeed:
**Upper apical edge lengths:
**Base edge lengths:
**Lower apical edge lengths (equal to upper edge lengths):
*The bipyramid with same base vertices, but with right symmetric apices also has its faces isosceles. Indeed:
**Upper apical edge lengths:
**Base edge length (equal to previous example):
**Lower apical edge lengths (equal to upper edge lengths):
In crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
, isotoxal right (symmetric) didigonal (8-faced), ditrigonal (12-faced), ditetragonal (16-faced), and dihexagonal (24-faced) bipyramids exist.
Scalenohedra
A scalenohedron is similar to a bipyramid; the difference is that the scalenohedra has a zig-zag pattern in the middle edges. It has two apices and basal vertices, faces, and edges; it is topologically identical to a -gonal bipyramid, but its basal vertices alternate in two rings above and below the center. All its faces arecongruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
scalene triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional ...
s, and it is isohedral. It can be seen as another type of a right symmetric di--gonal bipyramid, with a regular zigzag skew polygon base.
A regular right symmetric di--gonal scalenohedron has two-fold rotation axes through opposite basal mid-edges, reflection planes through opposite apical edges, an -fold rotation axis through apices, and a -fold rotation-reflection axis through apices (about which rotations-reflections globally preserve the solid), representing symmetry group of order . (If is odd, then there is an inversion symmetry about the center, corresponding to the rotation-reflection.)
Example with :
:A regular right symmetric ditrigonal scalenohedron has three similar vertical planes of symmetry inclined to one another at and intersecting in a (vertical) -fold rotation axis, three similar horizontal -fold rotation axes, each perpendicular to a plane of symmetry, a center of inversion symmetry, and a vertical -fold rotation-reflection axis.
Example with :
:A regular right symmetric didigonal scalenohedron has only one vertical and two horizontal -fold rotation axes, two vertical planes of symmetry, which bisect the angles between the horizontal pair of axes, and a vertical -fold rotation-reflection axis; it has no center of inversion symmetry.
For at most two particular values of the faces of such a scalenohedron may be isosceles.
Double example:
*The scalenohedron with regular zigzag skew -gon base vertices and right symmetric apices has its faces isosceles. Indeed:
**Upper apical edge lengths:
**Base edge length:
**Lower apical edge lengths (equal to upper edge lengths swapped):
*The scalenohedron with same base vertices, but with right symmetric apices also has its faces isosceles. Indeed:
**Upper apical edge lengths:
**Base edge length (equal to previous example):
**Lower apical edge lengths (equal to upper edge lengths swapped):
In crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
, regular right symmetric didigonal (-faced) and ditrigonal (-faced) scalenohedra exist.
The smallest geometric scalenohedra have eight faces, and are topologically identical to the regular octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
. In this case (), in crystallography, a regular right symmetric didigonal (-faced) scalenohedron is called a ''tetragonal scalenohedron''.
Let us temporarily focus on the regular right symmetric -faced scalenohedra with i.e.
Their two apices can be represented as and their four basal vertices as :
where is a parameter between and .
At , it is a regular octahedron; at , it has four pairs of coplanar faces, and merging these into four congruent isosceles triangles makes it a disphenoid
In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same ...
; for , it is concave.
If the -gon base is both isotoxal in-out and zigzag skew, then not all faces of the isotoxal right symmetric scalenohedron are congruent.
Example with five different edge lengths:
*The scalenohedron with isotoxal in-out zigzag skew -gon base vertices and right symmetric apices has congruent scalene upper faces, and congruent scalene lower faces, but not all its faces are congruent. Indeed:
**Upper apical edge lengths:
**Base edge length:
**Lower apical edge lengths:
For some particular values of , half the faces of such a scalenohedron may be isosceles or equilateral.
Example with three different edge lengths:
*The scalenohedron with isotoxal in-out zigzag skew -gon base vertices and right symmetric apices has congruent scalene upper faces, and congruent equilateral lower faces; thus not all its faces are congruent. Indeed:
**Upper apical edge lengths:
**Base edge length:
**Lower apical edge length(s):
Star bipyramids
A ''star'' bipyramid has astar polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can ...
base, and is self-intersecting.
A regular right symmetric star bipyramid has congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
isosceles
In geometry, an isosceles triangle () is a triangle that has two sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides ...
triangle faces, and is isohedral.
A -bipyramid has Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
.
4-polytopes with bipyramidal cells
The dual of the rectification of eachconvex regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six co ...
s is a cell-transitive 4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: Vertex (geometry), vertices, Edge (geo ...
with bipyramidal cells. In the following:
* is the apex vertex of the bipyramid;
* is an equator vertex;
* is the distance between adjacent vertices on the equator (equal to 1);
* is the apex-to-equator edge length;
* is the distance between the apices.
The bipyramid 4-polytope will have vertices where the apices of bipyramids meet. It will have vertices where the type vertices of bipyramids meet.
* bipyramids meet along each type edge.
* bipyramids meet along each type edge.
* is the cosine of the dihedral angle along an edge.
* is the cosine of the dihedral angle along an edge.
As cells must fit around an edge,
Other dimensions
polytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an ...
constructed from an -polytope ''base'' lying in a hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
, with every base vertex connected by an edge to two ''apex'' vertices. If the -polytope is a regular polytope and the apices are equidistant from its center along the line perpendicular to the base hyperplane, it will have identical pyramidal facets.
A 2-dimensional analog of a right symmetric bipyramid is formed by joining two congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
s base-to-base to form a rhombus
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhom ...
. More generally, a kite
A kite is a tethered heavier than air flight, heavier-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. Kites often have ...
is a 2-dimensional analog of a (possibly asymmetric) right bipyramid, and any quadrilateral is a 2-dimensional analog of a general bipyramid.
See also
* TrapezohedronNotes
Citations
Works cited
* Chapter 4: Duals of the Archimedean polyhedra, prisms and antiprisms *External links
* *The Uniform Polyhedra
The Encyclopedia of Polyhedra ** VRML model
(George Hart)
*
Try: "dP''n''", where ''n'' = 3, 4, 5, 6, ... Example: "dP4" is an octahedron. {{Polyhedron navigator Polyhedra