|
Scalenohedron
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually ''symmetric'', meaning the two pyramids are mirror images across their common base plane. When each apex (, the off-base vertices) of the bipyramid is on a line perpendicular to the base and passing through its center, it is a ''right'' bipyramid; otherwise it is ''oblique''. When the base is a regular polygon, the bipyramid is also called ''regular''. Definition and properties A bipyramid is a polyhedron constructed by fusing two pyramids which share the same polygonal base; a pyramid is in turn constructed by connecting each vertex of its base to a single new vertex (the apex) not lying in the plane of the base, for an gonal base forming triangular faces in addition to the base face. An gona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isohedral Figure
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its Face (geometry), faces are the same. More specifically, all faces must be not merely Congruence (geometry), congruent but must be ''transitive'', i.e. must lie within the same ''symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by Translation (geometry), translations, Rotation (mathematics), rotations, and/or Reflection (mathematics), reflections that maps onto . For this reason, Convex polytope, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an Parity (mathematics), even number of faces. The Dual polyhedron, dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
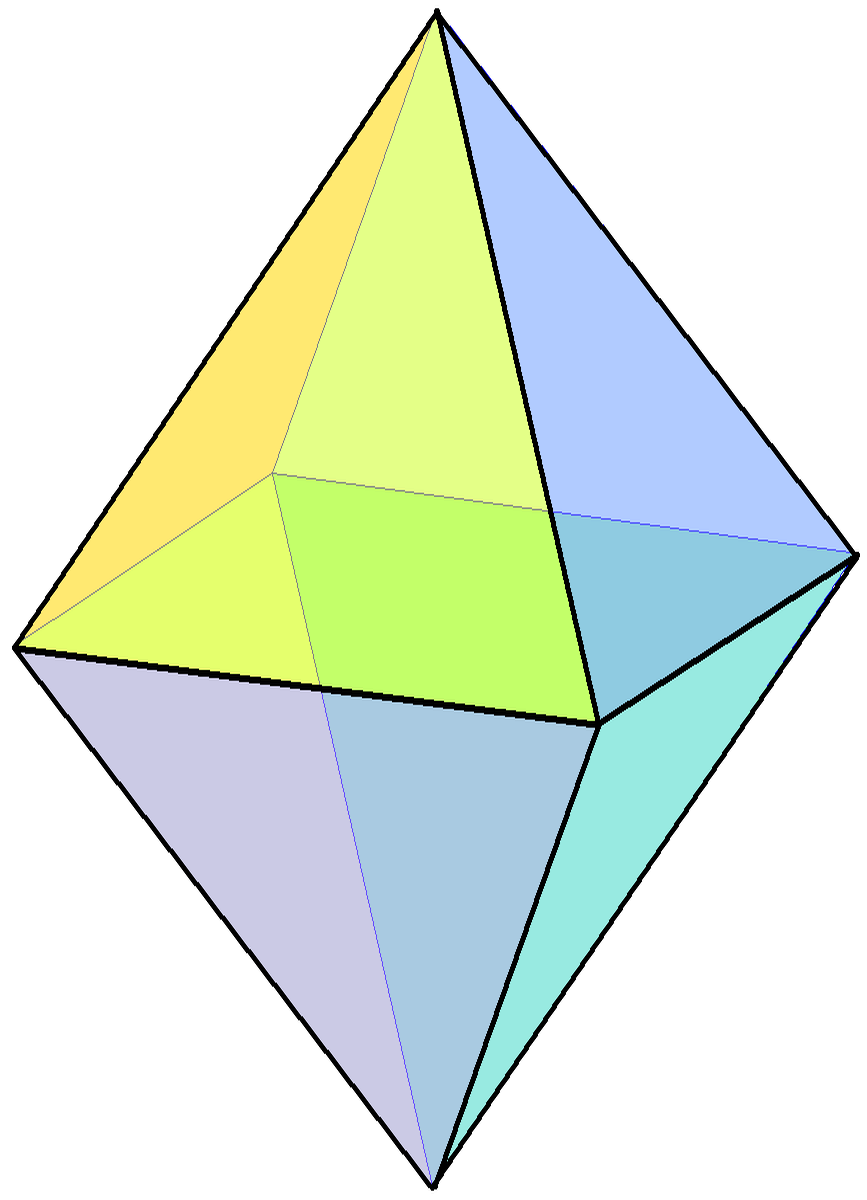
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation (mathematics)
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire -dimensional flat of fixed points in a - dimensional space. Mathematically, a rotation is a map. All rotations about a fixed point form a group under composition called the rotation group (of a particular space). But in mechanics and, more generally, in physics, this concept is frequently understood as a coordinate transformation (importantly, a transformation of an orthonormal basis), because for any motion of a body there is an inverse transformat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements, Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axis Of Symmetry
An axis (: axes) may refer to: Mathematics *A specific line (often a directed line) that plays an important role in some contexts. In particular: ** Coordinate axis of a coordinate system *** ''x''-axis, ''y''-axis, ''z''-axis, common names for the coordinate axes of a Cartesian coordinate system ** Axis of rotation ** Axis of symmetry ** Axis of a conic section Politics *Axis powers of World War II, 1936–1945. * Axis of evil (first used in 2002), U.S. President George W. Bush's description of Iran, Iraq, and North Korea *Axis of Resistance (first used in 2002), the Shia alliance of Iran, Syria, and Hezbollah * Axis of Upheaval (first used in 2024), foreign policy neologism of the Anti-western collaboration between Russia, China, Iran, and North Korea * Jakarta-Pyongyang-Peking Axis, diplomatic alignment and alliance between Indonesia, China, and North Korea during Sukarno's Presidency *Political spectrum, sometimes called an axis Science *Axis (anatomy), the second cerv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the n-gon, -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition The word "dihedral" comes from "di-" and "-hedron". The latter comes from the Greek word hédra, which means "face of a geometrical solid". Overall it thus refers to the two faces of a polygon. Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetry, rotational symmetries and n reflection symmetry, reflection symmetries. Usually, we take n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatic Symmetry
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2). Types There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation. ;Chiral: *''Dn'', 'n'',2sup>+, (22''n'') of order 2''n'' – dihedral symmetry or para-n-gonal group (abstract group: ''Dihn''). ;Achiral: *''Dnh'', 'n'',2 (*22''n'') of order 4''n'' – prismatic symmetry or full ortho-n-gonal group (abstract group: ''Dihn'' × ''Z''2). *''Dnd'' (or ''Dnv''), ''n'',2+ (2*''n'') of order 4''n'' – antiprismatic symmetry or full gyro-n-gonal group (abstract group: ''Dih''2''n''). For a given ''n'', all three have ''n''-fold rotational symmetry about one axis (rotation by an angle of 360°/''n'' does not change the object), and 2-fold rotational symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Cube-Octahedron
Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual number, a number system used in automatic differentiation * Dual (grammatical number), a grammatical category used in some languages * Dual county, a Gaelic games county which competes in both Gaelic football and hurling * Dual diagnosis, a psychiatric diagnosis of co-occurrence of substance abuse and a mental problem * Dual fertilization, simultaneous application of a P-type and N-type fertilizer * Dual impedance, electrical circuits that are the dual of each other * Dual SIM cellphone supporting use of two SIMs * Aerochute International Dual a two-seat Australian powered parachute design Acronyms and other uses * Dual (brand), a manufacturer of Hifi equipment * DUAL (cognitive architecture), an artificial intelligence design model * DUAL algor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (identical in shape and size) regular polygons (all angles congruent and all edge (geometry), edges congruent), and the same number of faces meet at each Vertex (geometry), vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the ''Timaeus (dialogue), Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |