right triangular prism on:
[Wikipedia]
[Google]
[Amazon]
 In
In
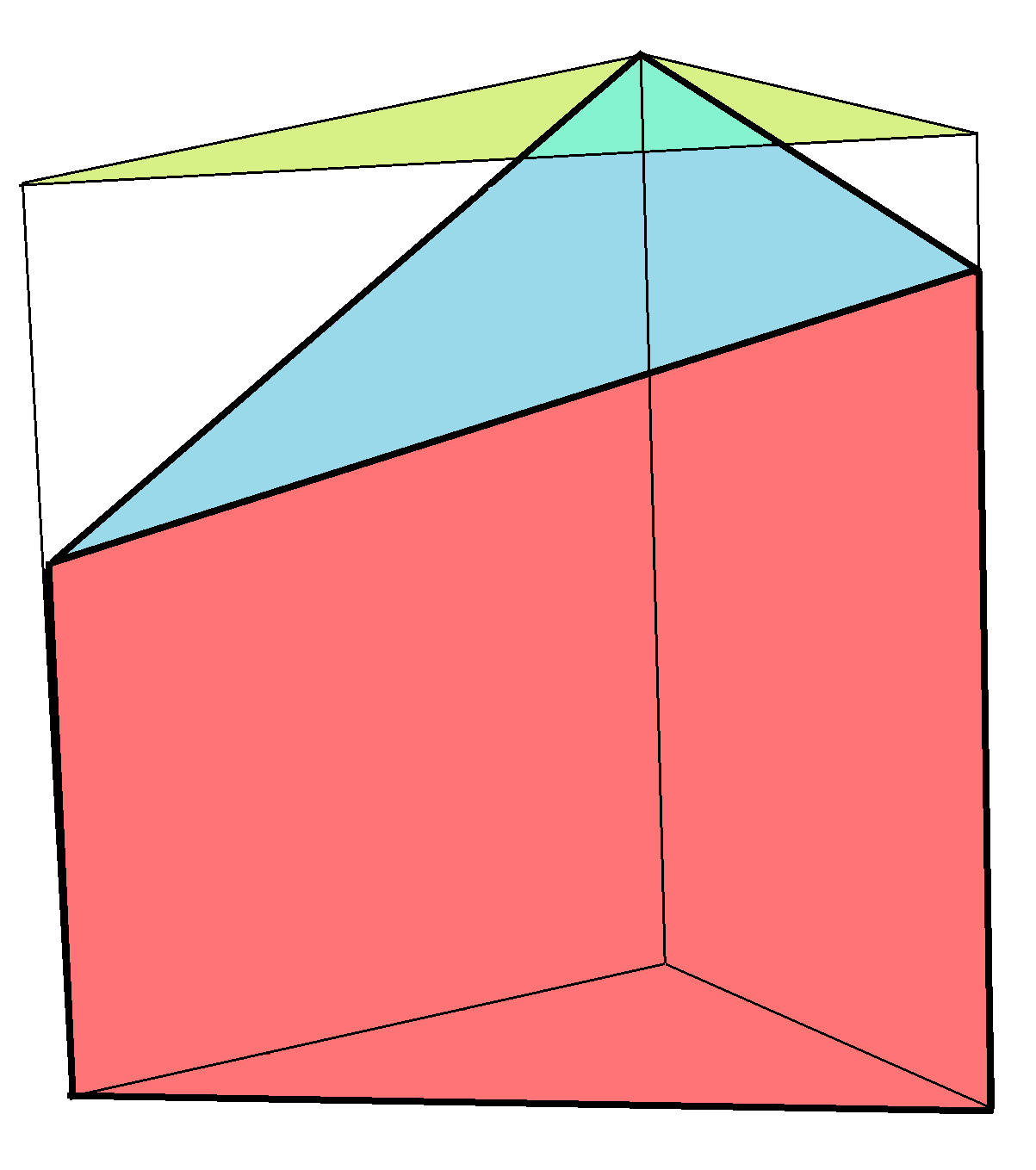 The volume of a truncated triangular prism with base area ''A'' and the three heights ''h''1, ''h''2, and ''h''3 is determined by
::
The volume of a truncated triangular prism with base area ''A'' and the three heights ''h''1, ''h''2, and ''h''3 is determined by
::

Interactive Polyhedron: Triangular Prism
Surface area and volume of a triangular prism
Prismatoid polyhedra Space-filling polyhedra
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a triangular prism is a three-sided prism; it is a polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
made of a triangular
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non-collinear, ...
base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containin ...
sides, otherwise it is ''oblique''. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.
Equivalently, it is a polyhedron of which two faces are parallel, while the surface normal
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve ...
s of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of eq ...
s. All cross-sections parallel to the base faces are the same triangle.
As a semiregular (or uniform) polyhedron
A right triangular prism is semiregular or, more generally, auniform polyhedron
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent.
Uniform polyhedra may be regular (if also ...
if the base faces are equilateral triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colli ...
s, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to mor ...
t. Alternately it can be seen as the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ ...
of a triangle and a line segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
, and represented by the product, The dual
Dual or Duals may refer to:
Paired/two things
* Dual (mathematics), a notion of paired concepts that mirror one another
** Dual (category theory), a formalization of mathematical duality
*** see more cases in :Duality theories
* Dual (grammatical ...
of a triangular prism is a triangular bipyramid
In geometry, the triangular bipyramid (or dipyramid) is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.
As the name suggests, i ...
.
The symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
of a right 3-sided prism with triangular base is ''D3h'' of order 12. The rotation group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. ...
is ''D3'' of order 6. The symmetry group does not contain inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
.
Volume
The volume of any prism is the product of the area of the base and the distance between the two bases. In this case the base is a triangle so we simply need to compute the area of the triangle and multiply this by the length of the prism: : where is the length of one side of the triangle, is the length of analtitude
Altitude or height (also sometimes known as depth) is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The exact definition and reference datum varies according to the context ...
drawn to that side, and is the distance between the triangular faces.
Truncated triangular prism
A ''truncated right triangular prism'' has one triangular face truncated (planed
Rural community development encompasses a range of approaches and activities that aim to improve the welfare and livelihoods of people living in rural areas. As a branch of community development, these approaches pay attention to social issues par ...
) at an oblique angle.
: The volume of a truncated triangular prism with base area ''A'' and the three heights ''h''1, ''h''2, and ''h''3 is determined by
::
The volume of a truncated triangular prism with base area ''A'' and the three heights ''h''1, ''h''2, and ''h''3 is determined by
::
Facetings
There are two full D3h symmetry facetings of a ''triangular prism'', both with 6isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ...
faces, one keeping the original top and bottom triangles, and one the original squares. Two lower C3v symmetry facetings have one base triangle, 3 lateral crossed square faces, and 3 isosceles triangle lateral faces.
Related polyhedra and tilings

Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and ,3Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
symmetry.
This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of fa ...
figures have (*n32) reflectional symmetry.
Compounds
There are 4 uniform compounds of triangular prisms: : Compound of four triangular prisms, compound of eight triangular prisms,compound of ten triangular prisms
This uniform polyhedron compound is a Chirality (mathematics), chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.
Related polyhedra
This compound shares its vertex a ...
, compound of twenty triangular prisms
This uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.
It results from composing the two enantiomorphs
In geometry, a figure is ch ...
.
Honeycombs
There are 9 uniform honeycombs that include triangular prism cells: :Gyroelongated alternated cubic honeycomb
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
Other names incl ...
, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb
The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed entirely of triangular prisms.
It is constructed from a triangular tiling extruded into pri ...
Related polytopes
The triangular prism is first in a dimensional series ofsemiregular polytope
In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as ''The Semiregular Polyt ...
s. Each progressive uniform polytope is constructed vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines ...
of the previous polytope. Thorold Gosset
John Herbert de Paz Thorold Gosset (16 October 1869 – December 1962) was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher, a ...
identified this series in 1900 as containing all regular polytope facets, containing all simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension ...
es and orthoplex
In geometry, a cross-polytope, hyperoctahedron, orthoplex, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahed ...
es (equilateral triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each oth ...
s and square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length a ...
s in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −121.
Four dimensional space
The triangular prism exists as cells of a number of four-dimensionaluniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
There are 47 non-prismatic convex uniform 4-polytopes. There ...
s, including:
See also
* Wedge (geometry)References
* {{mathworld , urlname = TriangularPrism , title = Triangular prismInteractive Polyhedron: Triangular Prism
Surface area and volume of a triangular prism
Prismatoid polyhedra Space-filling polyhedra