Regression Analysis

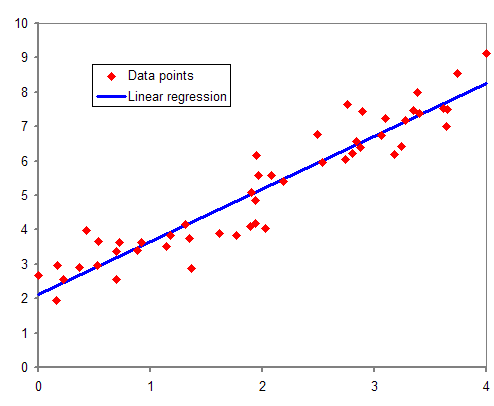In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ''outcome'' or ''response'' variable, or a ''label'' in machine learning parlance) and one or more error-free independent variables (often called ''regressors'', ''predictors'', ''covariates'', ''explanatory variables'' or ''features'').

The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters (e.g., quantile regression or Necessary Condition Analysis) or estimate the conditional expectation across a broader collection of non-linear models (e.g., nonparametric regression).

Regression analysis is primarily used for two conceptually distinct purposes. First, regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning. Second, in some situations regression analysis can be used to infer causal relationships between the independent and dependent variables. Importantly, regressions by themselves only reveal relationships between a dependent variable and a collection of independent variables in a fixed dataset. To use regressions for prediction or to infer causal relationships, respectively, a researcher must carefully justify why existing relationships have predictive power for a new context or why a relationship between two variables has a causal interpretation. The latter is especially important when researchers hope to estimate causal relationships using observational data.

History

The earliest regression form was seen in Isaac Newton's work in 1700 while studying equinoxes, being credited with introducing "an embryonic linear aggression analysis" as "Not only did he perform the averaging of a set of data, 50 years before Tobias Mayer, but summing the residuals to zero he ''forced'' the regression line to pass through the average point. He also distinguished between two inhomogeneous sets of data and might have thought of an ''optimal'' solution in terms of bias, though not in terms of effectiveness." He previously used an averaging method in his 1671 work on Newton's rings, which was unprecedented at the time.

The method of least squares was published by Legendre in 1805, A.M. Legendre
''Nouvelles méthodes pour la détermination des orbites des comètes''
Firmin Didot, Paris, 1805. "Sur la Méthode des moindres quarrés" appears as an appendix. and by Gauss in 1809.Chapter 1 of: Angrist, J. D., & Pischke, J. S. (2008). ''Mostly Harmless Econometrics: An Empiricist's Companion''. Princeton University Press. Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821, including a version of the Gauss–Markov theorem.

The term "regression" was coined by Francis Galton in the 19th century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).
For Galton, regression had only this biological meaning, but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context. In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925. Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher's assumption is closer to Gauss's formulation of 1821.

In the 1950s and 1960s, economists used electromechanical desk calculators to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.

Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression. Modern regression analysis is typically done with statistical and spreadsheet software packages on computers as well as on handheld scientific and graphing calculators.

Regression model

In practice, researchers first select a model they would like to estimate and then use their chosen method (e.g., ordinary least squares) to estimate the parameters of that model. Regression models involve the following components:
*The unknown parameters, often denoted as a scalar or vector $\beta$.
*The independent variables, which are observed in data and are often denoted as a vector $X_i$ (where $i$ denotes a row of data).
*The dependent variable, which are observed in data and often denoted using the scalar $Y_i$.
*The error terms, which are ''not'' directly observed in data and are often denoted using the scalar $e_i$.

In various fields of application, different terminologies are used in place of dependent and independent variables.

Most regression models propose that $Y_i$ is a function (regression function) of $X_i$ and $\beta$, with $e_i$ representing an additive error term that may stand in for un-modeled determinants of $Y_i$ or random statistical noise:

:$Y_i = f (X_i, \beta) + e_i$

Note that the independent variables $X_i$ are assumed to be free of error. This important assumption is often overlooked, although errors-in-variables models can be used when the independent variables are assumed to contain errors.

The researchers' goal is to estimate the function $f(X_i, \beta)$ that most closely fits the data. To carry out regression analysis, the form of the function $f$ must be specified. Sometimes the form of this function is based on knowledge about the relationship between $Y_i$ and $X_i$ that does not rely on the data. If no such knowledge is available, a flexible or convenient form for $f$ is chosen. For example, a simple univariate regression may propose $f(X_i, \beta) = \beta_0 + \beta_1 X_i$, suggesting that the researcher believes $Y_i = \beta_0 + \beta_1 X_i + e_i$ to be a reasonable approximation for the statistical process generating the data.

Once researchers determine their preferred statistical model, different forms of regression analysis provide tools to estimate the parameters $\beta$. For example, least squares (including its most common variant, ordinary least squares) finds the value of $\beta$ that minimizes the sum of squared errors $\sum_i (Y_i - f(X_i, \beta))^2$. A given regression method will ultimately provide an estimate of $\beta$, usually denoted $\hat$ to distinguish the estimate from the true (unknown) parameter value that generated the data. Using this estimate, the researcher can then use the ''fitted value'' $\hat = f(X_i,\hat)$ for prediction or to assess the accuracy of the model in explaining the data. Whether the researcher is intrinsically interested in the estimate $\hat$ or the predicted value $\hat$ will depend on context and their goals. As described in ordinary least squares, least squares is widely used because the estimated function $f(X_i, \hat)$ approximates the conditional expectation $E(Y_i, X_i)$. However, alternative variants (e.g., least absolute deviations or quantile regression) are useful when researchers want to model other functions $f(X_i,\beta)$.

It is important to note that there must be sufficient data to estimate a regression model. For example, suppose that a researcher has access to $N$ rows of data with one dependent and two independent variables: $(Y_i, X_, X_)$. Suppose further that the researcher wants to estimate a bivariate linear model via least squares: $Y_i = \beta_0 + \beta_1 X_ + \beta_2 X_ + e_i$. If the researcher only has access to $N=2$ data points, then they could find infinitely many combinations $(\hat_0, \hat_1, \hat_2)$ that explain the data equally well: any combination can be chosen that satisfies $\hat_i = \hat_0 + \hat_1 X_ + \hat_2 X_$, all of which lead to $\sum_i \hat_i^2 = \sum_i (\hat_i - (\hat_0 + \hat_1 X_ + \hat_2 X_))^2 = 0$ and are therefore valid solutions that minimize the sum of squared residuals. To understand why there are infinitely many options, note that the system of $N=2$ equations is to be solved for 3 unknowns, which makes the system underdetermined. Alternatively, one can visualize infinitely many 3-dimensional planes that go through $N=2$ fixed points.

More generally, to estimate a least squares model with $k$ distinct parameters, one must have $N \geq k$ distinct data points. If $N > k$, then there does not generally exist a set of parameters that will perfectly fit the data. The quantity $N-k$ appears often in regression analysis, and is referred to as the degrees of freedom in the model. Moreover, to estimate a least squares model, the independent variables $(X_, X_, ..., X_)$ must be linearly independent: one must ''not'' be able to reconstruct any of the independent variables by adding and multiplying the remaining independent variables. As discussed in ordinary least squares, this condition ensures that $X^X$ is an invertible matrix and therefore that a unique solution $\hat$ exists.

Underlying assumptions

By itself, a regression is simply a calculation using the data. In order to interpret the output of regression as a meaningful statistical quantity that measures real-world relationships, researchers often rely on a number of classical assumptions. These assumptions often include:

*The sample is representative of the population at large.
*The independent variables are measured without error.
*Deviations from the model have an expected value of zero, conditional on covariates: $E(e_i , X_i) = 0$
*The variance of the residuals $e_i$ is constant across observations (homoscedasticity).
* The residuals $e_i$ are uncorrelated with one another. Mathematically, the variance–covariance matrix of the errors is diagonal.

A handful of conditions are sufficient for the least-squares estimator to possess desirable properties: in particular, the Gauss–Markov assumptions imply that the parameter estimates will be unbiased, consistent, and efficient in the class of linear unbiased estimators. Practitioners have developed a variety of methods to maintain some or all of these desirable properties in real-world settings, because these classical assumptions are unlikely to hold exactly. For example, modeling errors-in-variables can lead to reasonable estimates independent variables are measured with errors. Heteroscedasticity-consistent standard errors allow the variance of $e_i$ to change across values of $X_i$. Correlated errors that exist within subsets of the data or follow specific patterns can be handled using ''clustered standard errors, geographic weighted regression'', or Newey–West standard errors, among other techniques. When rows of data correspond to locations in space, the choice of how to model $e_i$ within geographic units can have important consequences. The subfield of econometrics is largely focused on developing techniques that allow researchers to make reasonable real-world conclusions in real-world settings, where classical assumptions do not hold exactly.

Linear regression

In linear regression, the model specification is that the dependent variable, $y_i$ is a linear combination of the ''parameters'' (but need not be linear in the ''independent variables''). For example, in simple linear regression for modeling $n$ data points there is one independent variable: $x_i$, and two parameters, $\beta_0$ and $\beta_1$:

:straight line: $y_i=\beta_0 +\beta_1 x_i +\varepsilon_i,\quad i=1,\dots,n.\!$

In multiple linear regression, there are several independent variables or functions of independent variables.

Adding a term in $x_i^2$ to the preceding regression gives:

:parabola: $y_i=\beta_0 +\beta_1 x_i +\beta_2 x_i^2+\varepsilon_i,\ i=1,\dots,n.\!$

This is still linear regression; although the expression on the right hand side is quadratic in the independent variable $x_i$, it is linear in the parameters $\beta_0$, $\beta_1$ and $\beta_2.$

In both cases, $\varepsilon_i$ is an error term and the subscript $i$ indexes a particular observation.

Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:

: $\widehat_i = \widehat_0 + \widehat_1 x_i.$

The residual, $e_i = y_i - \widehat_i$, is the difference between the value of the dependent variable predicted by the model, $\widehat_i$, and the true value of the dependent variable, $y_i$. One method of estimation is ordinary least squares. This method obtains parameter estimates that minimize the sum of squared residuals, SSR:

:$SSR=\sum_^n e_i^2$

Minimization of this function results in a set of normal equations, a set of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, $\widehat_0, \widehat_1$.

In the case of simple regression, the formulas for the least squares estimates are

:$\widehat_1=\frac$
:$\widehat_0=\bar-\widehat_1\bar$

where $\bar$ is the mean (average) of the $x$ values and $\bar$ is the mean of the $y$ values.

Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:

: $\hat^2_\varepsilon = \frac$

This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same data, $(n-p)$ for $p$ regressors or $(n-p-1)$ if an intercept is used. In this case, $p=1$ so the denominator is $n-2$.

The standard errors of the parameter estimates are given by

:$\hat\sigma_=\hat\sigma_ \sqrt$

:$\hat\sigma_=\hat\sigma_\varepsilon \sqrt=\hat\sigma_ \sqrt.$

Under the further assumption that the population error term is normally distributed, the researcher can use these estimated standard errors to create confidence intervals and conduct hypothesis tests about the population parameters.

General linear model

In the more general multiple regression model, there are $p$ independent variables:

: $y_i = \beta_1 x_ + \beta_2 x_ + \cdots + \beta_p x_ + \varepsilon_i, \,$

where $x_$ is the $i$-th observation on the $j$-th independent variable.
If the first independent variable takes the value 1 for all $i$, $x_ = 1$, then $\beta_1$ is called the regression intercept.

The least squares parameter estimates are obtained from $p$ normal equations. The residual can be written as

:$\varepsilon_i=y_i - \hat\beta_1 x_ - \cdots - \hat\beta_p x_.$

The normal equations are

:$\sum_^n \sum_^p x_x_\hat \beta_k=\sum_^n x_y_i,\ j=1,\dots,p.\,$

In matrix notation, the normal equations are written as

:$\mathbf,\,$

where the $ij$ element of $\mathbf X$ is $x_$, the $i$ element of the column vector $Y$ is $y_i$, and the $j$ element of $\hat \boldsymbol \beta$ is $\hat \beta_j$. Thus $\mathbf X$ is $n \times p$, $Y$ is $n \times 1$, and $\hat \boldsymbol \beta$ is $p \times 1$. The solution is

:$\mathbf.\,$

Diagnostics

Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.

Interpretations of these diagnostic tests rest heavily on the model's assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model's assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.

Limited dependent variables

Limited dependent variables, which are response variables that are categorical or constrained to fall only in a certain range, often arise in econometrics.

The response variable may be non-continuous ("limited" to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest.

An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used.

Nonlinear regression

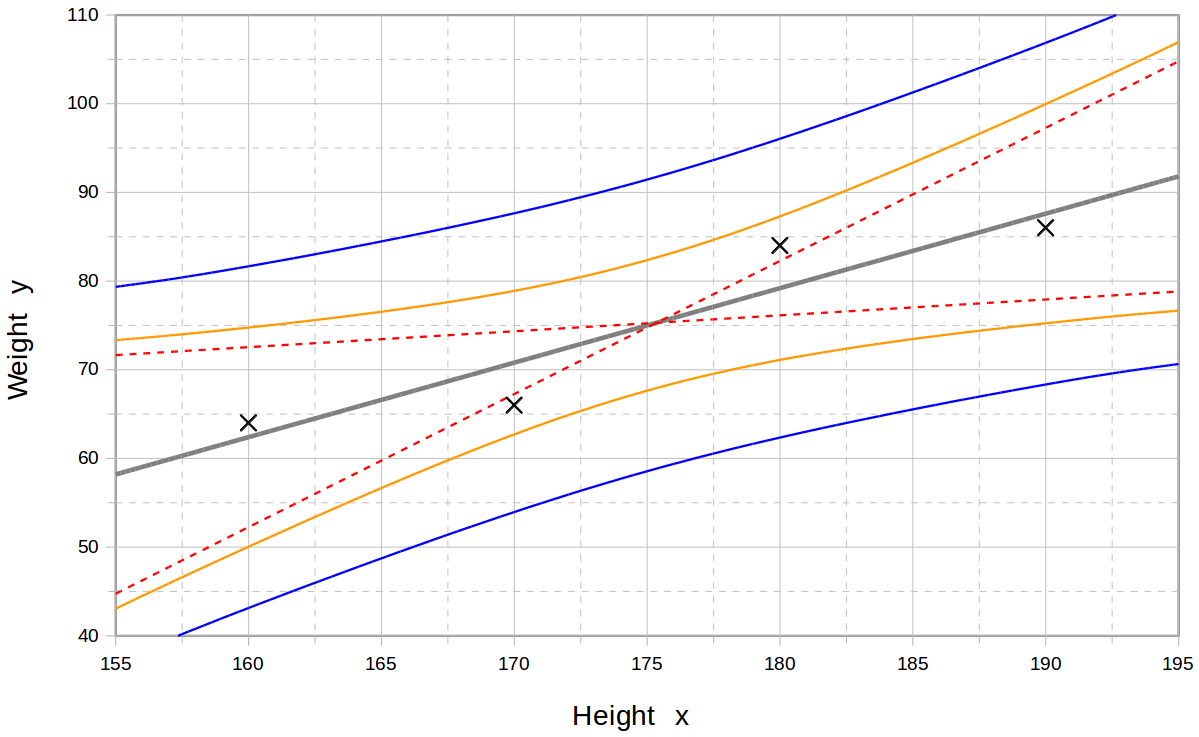
When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.

Prediction (interpolation and extrapolation)

Regression models ''predict'' a value of the ''Y'' variable given known values of the ''X'' variables. Prediction the range of values in the dataset used for model-fitting is known informally as ''interpolation''. Prediction this range of the data is known as ''extrapolation''. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.

A ''prediction interval'' that represents the uncertainty may accompany the point prediction. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.

For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.

Model selection

The assumption of a particular form for the relation between ''Y'' and ''X'' is another source of uncertainty. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is "realistic" (or in accord with what is known).

Power and sample size calculations

There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One method conjectured by Good and Hardin is $N=m^n$, where $N$ is the sample size, $n$ is the number of independent variables and $m$ is the number of observations needed to reach the desired precision if the model had only one independent variable. For example, a researcher is building a linear regression model using a dataset that contains 1000 patients ($N$). If the researcher decides that five observations are needed to precisely define a straight line ($m$), then the maximum number of independent variables ($n$) the model can support is 4, because

: $\frac\approx4.29$.

Other methods

Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:
* Bayesian methods, e.g. Bayesian linear regression
* Percentage regression, for situations where reducing ''percentage'' errors is deemed more appropriate.
* Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
* Nonparametric regression, requires a large number of observations and is computationally intensive
* Scenario optimization, leading to interval predictor models

Software

All major statistical software packages perform least squares regression analysis and inference. Simple linear regression and multiple regression using least squares can be done in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized. Different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for use in fields such as survey analysis and neuroimaging.

See also

* Anscombe's quartet
* Curve fitting
* Estimation theory
* Forecasting
* Fraction of variance unexplained
* Function approximation
* Generalized linear model
* Kriging (a linear least squares estimation algorithm)
* Local regression
* Modifiable areal unit problem
* Multivariate adaptive regression spline
* Multivariate normal distribution
* Pearson correlation coefficient
* Quasi-variance
* Prediction interval
* Regression validation
* Robust regression
* Segmented regression
* Signal processing
* Stepwise regression
* Taxicab geometry
* Linear trend estimation

References

Further reading

* William H. Kruskal and Judith M. Tanur, ed. (1978), "Linear Hypotheses," ''International Encyclopedia of Statistics''. Free Press, v. 1,
:Evan J. Williams, "I. Regression," pp. 523–41.
: Julian C. Stanley, "II. Analysis of Variance," pp. 541–554.
* Lindley, D.V. (1987). "Regression and correlation analysis," New Palgrave: A Dictionary of Economics, v. 4, pp. 120–23.
* Birkes, David and Dodge, Y., ''Alternative Methods of Regression''.
* Chatfield, C. (1993)
Calculating Interval Forecasts
" ''Journal of Business and Economic Statistics,'' 11. pp. 121–135.
*
* Fox, J. (1997). ''Applied Regression Analysis, Linear Models and Related Methods.'' Sage
* Hardle, W., ''Applied Nonparametric Regression'' (1990),
*
* A. Sen, M. Srivastava, ''Regression Analysis — Theory, Methods, and Applications'', Springer-Verlag, Berlin, 2011 (4th printing).
* T. Strutz: ''Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond)''. Vieweg+Teubner, .
* Stulp, Freek, and Olivier Sigaud. ''Many Regression Algorithms, One Unified Model: A Review.'' Neural Networks, vol. 69, Sept. 2015, pp. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
* Malakooti, B. (2013)
Operations and Production Systems with Multiple Objectives
John Wiley & Sons.
*

External links

*


– basic history and references

What is multiple regression used for?
– Multiple regression


– how linear regression mistakes can appear when Y-range is much smaller than X-range

{{DEFAULTSORT:Regression Analysis