 In
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a quasiconvex function is a real-valued function defined on an interval or on a convex subset
In geometry, a set of points is convex if it contains every line segment between two points in the set.
For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is n ...
of a real vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
such that the inverse image
In mathematics, for a function f: X \to Y, the image of an input value x is the single output value produced by f when passed x. The preimage of an output value y is the set of input values that produce y.
More generally, evaluating f at each ...
of any set of the form is a convex set
In geometry, a set of points is convex if it contains every line segment between two points in the set.
For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is n ...
. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.
Quasiconvexity is a more general property than convexity in that all convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
s are also quasiconvex, but not all quasiconvex functions are convex. ''Univariate
In mathematics, a univariate object is an expression (mathematics), expression, equation, function (mathematics), function or polynomial involving only one Variable (mathematics), variable. Objects involving more than one variable are ''wikt:multi ...
'' unimodal
In mathematics, unimodality means possessing a unique mode. More generally, unimodality means there is only a single highest value, somehow defined, of some mathematical object.
Unimodal probability distribution
In statistics, a unimodal p ...
functions are quasiconvex or quasiconcave, however this is not necessarily the case for functions with multiple arguments
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persua ...
. For example, the 2-dimensional Rosenbrock function is unimodal but not quasiconvex and functions with star-convex sublevel sets can be unimodal without being quasiconvex.
Definition and properties
A function defined on a convex subset of a real vector space is quasiconvex if for all and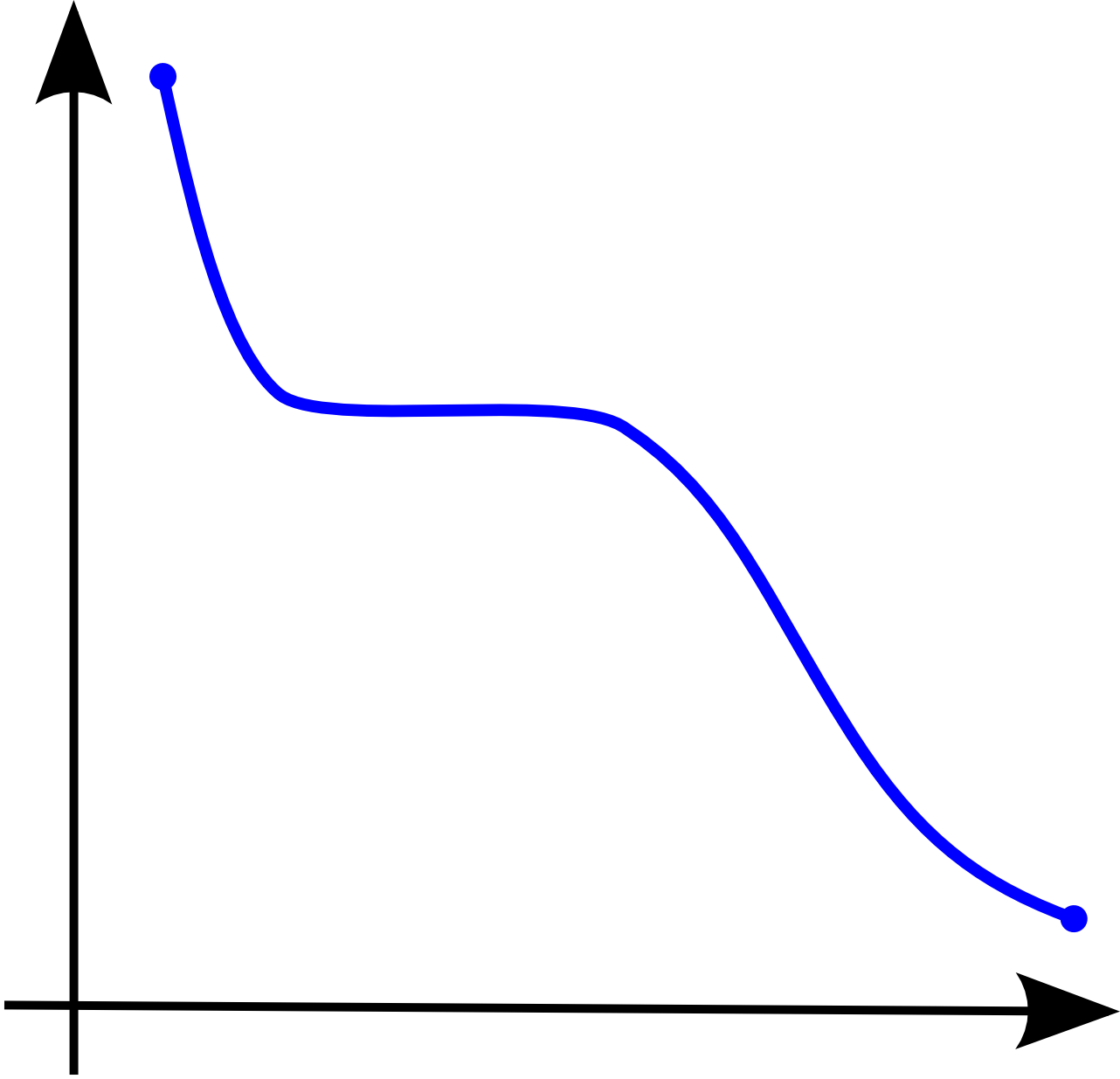
 An alternative way (see introduction) of defining a quasi-convex function
An alternative way (see introduction) of defining a quasi-convex function Applications
Quasiconvex functions have applications inmathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
, in mathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
, and in game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
.
Mathematical optimization
In nonlinear optimization, quasiconvex programming studiesiterative method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an " ...
s that converge to a minimum (if one exists) for quasiconvex functions. Quasiconvex programming is a generalization of convex programming. Quasiconvex programming is used in the solution of "surrogate" dual problem
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then th ...
s, whose biduals provide quasiconvex closures of the primal problem, which therefore provide tighter bounds than do the convex closures provided by Lagrangian dual problems. In theory
A theory is a systematic and rational form of abstract thinking about a phenomenon, or the conclusions derived from such thinking. It involves contemplative and logical reasoning, often supported by processes such as observation, experimentation, ...
, quasiconvex programming and convex programming problems can be solved in reasonable amount of time, where the number of iterations grows like a polynomial in the dimension of the problem (and in the reciprocal of the approximation error tolerated); however, such theoretically "efficient" methods use "divergent-series" step size rules, which were first developed for classical subgradient methods. Classical subgradient methods using divergent-series rules are much slower than modern methods of convex minimization, such as subgradient projection methods, bundle method
Subgradient methods are convex optimization methods which use Subderivative, subderivatives. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable object ...
s of descent, and nonsmooth filter methods.
Economics and partial differential equations: Minimax theorems
Inmicroeconomics
Microeconomics is a branch of economics that studies the behavior of individuals and Theory of the firm, firms in making decisions regarding the allocation of scarcity, scarce resources and the interactions among these individuals and firms. M ...
, quasiconcave utility function
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.
* In a Normative economics, normative context, utility refers to a goal or ob ...
s imply that consumers have convex preferences
In economics, convex preferences are an individual's ordering of various outcomes, typically with regard to the amounts of various goods consumed, with the property that, roughly speaking, "averages are better than the extremes". This implies that ...
. Quasiconvex functions are important
also in game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
, industrial organization
In economics, industrial organization is a field that builds on the theory of the firm by examining the structure of (and, therefore, the boundaries between) firms and markets. Industrial organization adds real-world complications to the per ...
, and general equilibrium theory
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an ov ...
, particularly for applications of Sion's minimax theorem. Generalizing a minimax theorem
In the mathematical area of game theory and of convex optimization, a minimax theorem is a theorem that claims that
: \max_ \min_ f(x,y) = \min_ \max_f(x,y)
under certain conditions on the sets X and Y and on the function f. It is always true that ...
of John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
, Sion's theorem is also used in the theory of partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s.
Preservation of quasiconvexity
Operations preserving quasiconvexity
* maximum of quasiconvex functions (i.e.Operations not preserving quasiconvexity
* The sum of quasiconvex functions defined on ''the same domain'' need not be quasiconvex: In other words, ifmathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
.
Examples
* Every convex function is quasiconvex. * A concave function can be quasiconvex. For example,monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of or ...
is both quasiconvex and quasiconcave. More generally, a function which decreases up to a point and increases from that point on is quasiconvex (compare unimodality).
*The floor function
In mathematics, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or eq ...
See also
*Convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
* Concave function
In mathematics, a concave function is one for which the function value at any convex combination of elements in the domain is greater than or equal to that convex combination of those domain elements. Equivalently, a concave function is any funct ...
* Logarithmically concave function
In convex analysis, a non-negative function is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it satisfies the inequality
:
f(\theta x + (1 - \theta) y) \geq f(x)^ f(y)^
for all and . If is stri ...
* Pseudoconvexity in the sense of several complex variables (not generalized convexity)
* Pseudoconvex function
* Invex function
* Concavification
References
External links
SION, M., "On general minimax theorems", Pacific J. Math. 8 (1958), 171-176.
Mathematical programming glossary
Concave and Quasi-Concave Functions
- by Charles Wilson, NYU Department of Economics
Quasiconcavity and quasiconvexity
- by Martin J. Osborne,
University of Toronto
The University of Toronto (UToronto or U of T) is a public university, public research university whose main campus is located on the grounds that surround Queen's Park (Toronto), Queen's Park in Toronto, Ontario, Canada. It was founded by ...
Department of Economics
{{Convex analysis and variational analysis
Convex analysis
Convex optimization
Generalized convexity
Real analysis
Types of functions