 In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a conve ...
of a real vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called '' vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but ...
such that the inverse image of any set of the form is a convex set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex ...
. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.
All convex functions are also quasiconvex, but not all quasiconvex functions are convex, so quasiconvexity is a generalization of convexity. '' Univariate'' unimodal
In mathematics, unimodality means possessing a unique mode. More generally, unimodality means there is only a single highest value, somehow defined, of some mathematical object.
Unimodal probability distribution
In statistics, a unimodal pr ...
functions are quasiconvex or quasiconcave, however this is not necessarily the case for functions with multiple arguments
An argument is a statement or group of statements called premises intended to determine the degree of truth or acceptability of another statement called conclusion. Arguments can be studied from three main perspectives: the logical, the dialectic ...
. For example, the 2-dimensional Rosenbrock function
In mathematical optimization, the Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is used as a performance test problem for optimization algorithms. It is also known as Rosenbrock's valley or Rose ...
is unimodal but not quasiconvex and functions with star-convex
In geometry, a set S in the Euclidean space \R^n is called a star domain (or star-convex set, star-shaped set or radially convex set) if there exists an s_0 \in S such that for all s \in S, the line segment from s_0 to s lies in S. This defini ...
sublevel sets can be unimodal without being quasiconvex.
Definition and properties
A function defined on a convex subset of a real vector space is quasiconvex if for all and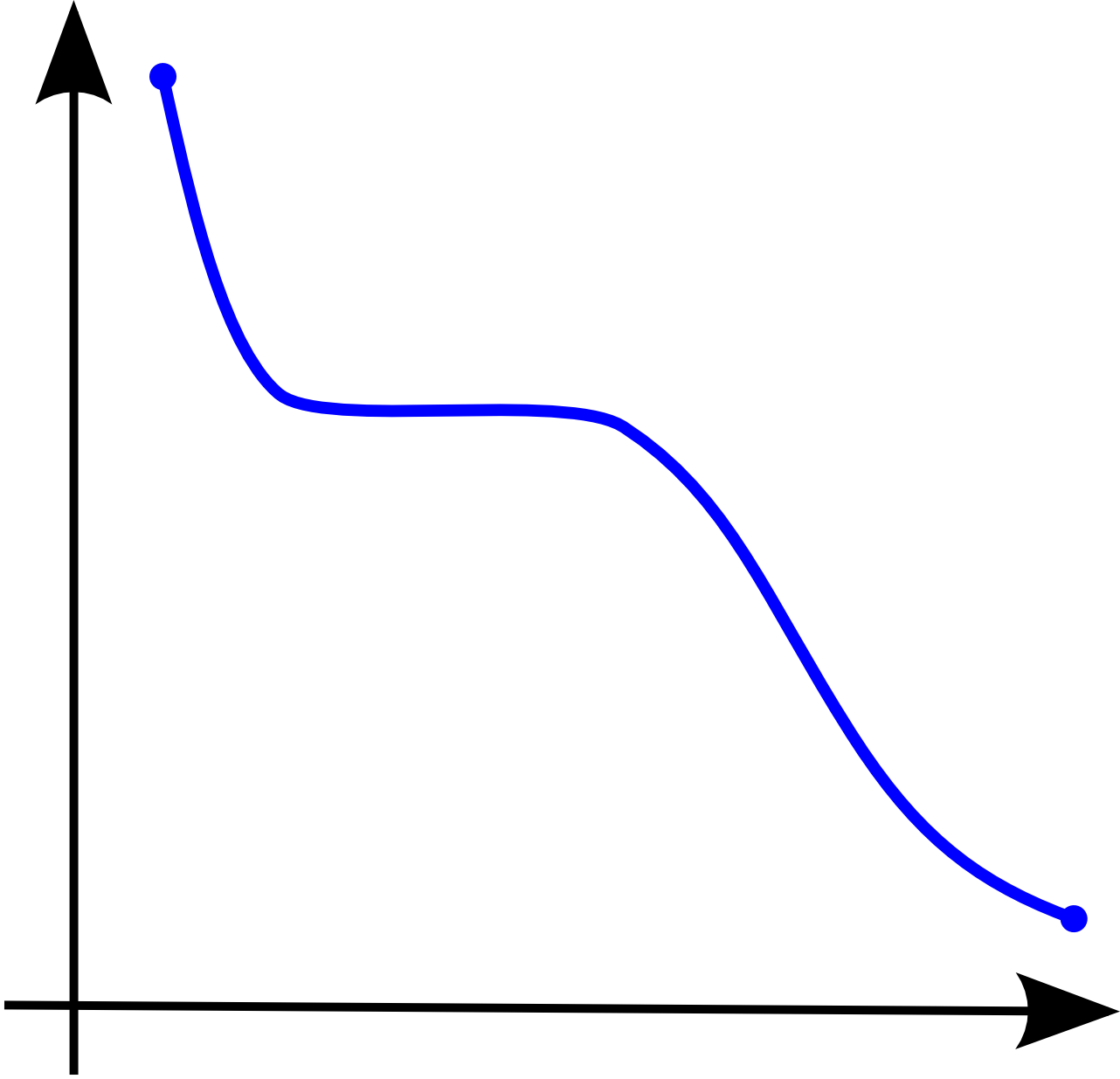
 An alternative way (see introduction) of defining a quasi-convex function
An alternative way (see introduction) of defining a quasi-convex function lower contour set In mathematics, contour sets generalize and formalize the everyday notions of
*everything superior to something
*everything superior or equivalent to something
*everything inferior to something
*everything inferior or equivalent to something.
For ...
s, while a (strictly) quasiconcave function has (strictly) convex upper contour set In mathematics, contour sets generalize and formalize the everyday notions of
*everything superior to something
*everything superior or equivalent to something
*everything inferior to something
*everything inferior or equivalent to something.
For ...
s.
A function that is both quasiconvex and quasiconcave is quasilinear.
A particular case of quasi-concavity, if Applications
Quasiconvex functions have applications inmathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (m ...
, in mathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
, and in game theory and economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analy ...
.
Mathematical optimization
In nonlinear optimization, quasiconvex programming studiesiterative method
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''n''-th approximation is derived from the pre ...
s that converge to a minimum (if one exists) for quasiconvex functions. Quasiconvex programming is a generalization of convex programming. Quasiconvex programming is used in the solution of "surrogate" dual problem
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then t ...
s, whose biduals provide quasiconvex closures of the primal problem, which therefore provide tighter bounds than do the convex closures provided by Lagrangian dual problems. In theory
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may ...
, quasiconvex programming and convex programming problems can be solved in reasonable amount of time, where the number of iterations grows like a polynomial in the dimension of the problem (and in the reciprocal of the approximation error tolerated); however, such theoretically "efficient" methods use "divergent-series" stepsize rules, which were first developed for classical subgradient method Subgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective funct ...
s. Classical subgradient methods using divergent-series rules are much slower than modern methods of convex minimization, such as subgradient projection methods, bundle method Subgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective funct ...
s of descent, and nonsmooth filter methods.
Economics and partial differential equations: Minimax theorems
In microeconomics, quasiconcaveutility function
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosoph ...
s imply that consumers have convex preferences. Quasiconvex functions are important
also in game theory, industrial organization
In economics, industrial organization is a field that builds on the theory of the firm by examining the structure of (and, therefore, the boundaries between) firms and markets. Industrial organization adds real-world complications to the perfe ...
, and general equilibrium theory
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an ov ...
, particularly for applications of Sion's minimax theorem
In mathematics, and in particular game theory, Sion's minimax theorem is a generalization of John von Neumann's minimax theorem, named after Maurice Sion.
It states:
Let X be a compact convex subset of a linear topological space and Y a convex su ...
. Generalizing a minimax theorem of John von Neumann
John von Neumann (; hu, Neumann János Lajos, ; December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. He was regarded as having perhaps the widest cove ...
, Sion's theorem is also used in the theory of partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to ...
s.
Preservation of quasiconvexity
Operations preserving quasiconvexity
* maximum of quasiconvex functions (i.e.Operations not preserving quasiconvexity
* The sum of quasiconvex functions defined on ''the same domain'' need not be quasiconvex: In other words, ifmathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
.
Examples
* Every convex function is quasiconvex. * A concave function can be quasiconvex. For example,monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of ord ...
is both quasiconvex and quasiconcave. More generally, a function which decreases up to a point and increases from that point on is quasiconvex (compare unimodality).
*The floor function See also
* Convex function *Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.
Definition
A real-valued function f on an ...
* Logarithmically concave function
* Pseudoconvexity in the sense of several complex variables (not generalized convexity)
* Pseudoconvex function
* Invex function In vector calculus, an invex function is a differentiable function f from \mathbb^n to \mathbb for which there exists a vector valued function \eta such that
:f(x) - f(u) \geq \eta(x, u) \cdot \nabla f(u), \,
for all ''x'' and ''u''.
Invex funct ...
* Concavification
References
External links
SION, M., "On general minimax theorems", Pacific J. Math. 8 (1958), 171-176.
Mathematical programming glossary
Concave and Quasi-Concave Functions
- by Charles Wilson, NYU Department of Economics
Quasiconcavity and quasiconvexity
- by Martin J. Osborne,
University of Toronto
The University of Toronto (UToronto or U of T) is a public research university in Toronto, Ontario, Canada, located on the grounds that surround Queen's Park. It was founded by royal charter in 1827 as King's College, the first institu ...
Department of Economics
{{Convex analysis and variational analysis
Convex analysis
Convex optimization
Generalized convexity
Real analysis
Types of functions