Quantum Systems

Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.

Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales.

Quantum systems have bound states that are quantized to discrete values of energy, momentum, angular momentum, and other quantities, in contrast to classical systems where these quantities can be measured continuously. Measurements of quantum systems show characteristics of both particles and waves (wave–particle duality), and there are limits to how accurately the value of a physical quantity can be predicted prior to its measurement, given a complete set of initial conditions (the uncertainty principle).

Quantum mechanics arose gradually from theories to explain observations that could not be reconciled with classical physics, such as Max Planck's solution in 1900 to the black-body radiation problem, and the correspondence between energy and frequency in Albert Einstein's 1905 paper, which explained the photoelectric effect. These early attempts to understand microscopic phenomena, now known as the "old quantum theory", led to the full development of quantum mechanics in the mid-1920s by Niels Bohr, Erwin Schrödinger, Werner Heisenberg, Max Born, Paul Dirac and others. The modern theory is formulated in various specially developed mathematical formalisms. In one of them, a mathematical entity called the wave function provides information, in the form of probability amplitudes, about what measurements of a particle's energy, momentum, and other physical properties may yield.

Overview and fundamental concepts

Quantum mechanics allows the calculation of properties and behaviour of physical systems. It is typically applied to microscopic systems: molecules, atoms and subatomic particles. It has been demonstrated to hold for complex molecules with thousands of atoms, but its application to human beings raises philosophical problems, such as Wigner's friend, and its application to the universe as a whole remains speculative. Predictions of quantum mechanics have been verified experimentally to an extremely high degree of accuracy. For example, the refinement of quantum mechanics for the interaction of light and matter, known as quantum electrodynamics (QED), has been shown to agree with experiment to within 1 part in 10¹² when predicting the magnetic properties of an electron.

A fundamental feature of the theory is that it usually cannot predict with certainty what will happen, but only give probabilities. Mathematically, a probability is found by taking the square of the absolute value of a complex number, known as a probability amplitude. This is known as the Born rule, named after physicist Max Born. For example, a quantum particle like an electron can be described by a wave function, which associates to each point in space a probability amplitude. Applying the Born rule to these amplitudes gives a probability density function for the position that the electron will be found to have when an experiment is performed to measure it. This is the best the theory can do; it cannot say for certain where the electron will be found. The Schrödinger equation relates the collection of probability amplitudes that pertain to one moment of time to the collection of probability amplitudes that pertain to another.

One consequence of the mathematical rules of quantum mechanics is a tradeoff in predictability between measurable quantities. The most famous form of this uncertainty principle says that no matter how a quantum particle is prepared or how carefully experiments upon it are arranged, it is impossible to have a precise prediction for a measurement of its position and also at the same time for a measurement of its momentum.

Another consequence of the mathematical rules of quantum mechanics is the phenomenon of quantum interference, which is often illustrated with the double-slit experiment. In the basic version of this experiment, a coherent light source, such as a laser beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate. The wave nature of light causes the light waves passing through the two slits to interfere, producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles. However, the light is always found to be absorbed at the screen at discrete points, as individual particles rather than waves; the interference pattern appears via the varying density of these particle hits on the screen. Furthermore, versions of the experiment that include detectors at the slits find that each detected photon passes through one slit (as would a classical particle), and not through both slits (as would a wave). However, such experiments demonstrate that particles do not form the interference pattern if one detects which slit they pass through. This behavior is known as wave–particle duality. In addition to light, electrons, atoms, and molecules are all found to exhibit the same dual behavior when fired towards a double slit.

Another non-classical phenomenon predicted by quantum mechanics is quantum tunnelling: a particle that goes up against a potential barrier can cross it, even if its kinetic energy is smaller than the maximum of the potential. In classical mechanics this particle would be trapped. Quantum tunnelling has several important consequences, enabling radioactive decay, nuclear fusion in stars, and applications such as scanning tunnelling microscopy, tunnel diode and tunnel field-effect transistor.

When quantum systems interact, the result can be the creation of quantum entanglement: their properties become so intertwined that a description of the whole solely in terms of the individual parts is no longer possible. Erwin Schrödinger called entanglement "...the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought". Quantum entanglement enables quantum computing and is part of quantum communication protocols, such as quantum key distribution and superdense coding. Contrary to popular misconception, entanglement does not allow sending signals faster than light, as demonstrated by the no-communication theorem.

Another possibility opened by entanglement is testing for " hidden variables", hypothetical properties more fundamental than the quantities addressed in quantum theory itself, knowledge of which would allow more exact predictions than quantum theory provides. A collection of results, most significantly Bell's theorem, have demonstrated that broad classes of such hidden-variable theories are in fact incompatible with quantum physics. According to Bell's theorem, if nature actually operates in accord with any theory of local hidden variables, then the results of a Bell test will be constrained in a particular, quantifiable way. Many Bell tests have been performed and they have shown results incompatible with the constraints imposed by local hidden variables.

It is not possible to present these concepts in more than a superficial way without introducing the mathematics involved; understanding quantum mechanics requires not only manipulating complex numbers, but also linear algebra, differential equations, group theory, and other more advanced subjects. Accordingly, this article will present a mathematical formulation of quantum mechanics and survey its application to some useful and oft-studied examples.

Mathematical formulation

In the mathematically rigorous formulation of quantum mechanics, the state of a quantum mechanical system is a vector $\psi$ belonging to a ( separable) complex Hilbert space $\mathcal H$. This vector is postulated to be normalized under the Hilbert space inner product, that is, it obeys $\langle \psi,\psi \rangle = 1$, and it is well-defined up to a complex number of modulus 1 (the global phase), that is, $\psi$ and $e^\psi$ represent the same physical system. In other words, the possible states are points in the projective space of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system – for example, for describing position and momentum the Hilbert space is the space of complex square-integrable functions $L^2(\mathbb C)$, while the Hilbert space for the spin of a single proton is simply the space of two-dimensional complex vectors $\mathbb C^2$ with the usual inner product.

Physical quantities of interestposition, momentum, energy, spinare represented by observables, which are Hermitian (more precisely, self-adjoint) linear operators acting on the Hilbert space. A quantum state can be an eigenvector of an observable, in which case it is called an eigenstate, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. More generally, a quantum state will be a linear combination of the eigenstates, known as a quantum superposition. When an observable is measured, the result will be one of its eigenvalues with probability given by the Born rule: in the simplest case the eigenvalue $\lambda$ is non-degenerate and the probability is given by $, \langle \vec\lambda,\psi\rangle, ^2$, where $\vec\lambda$ is its associated unit-length eigenvector. More generally, the eigenvalue is degenerate and the probability is given by $\langle \psi,P_\lambda\psi\rangle$, where $P_\lambda$ is the projector onto its associated eigenspace. In the continuous case, these formulas give instead the probability density.

After the measurement, if result $\lambda$ was obtained, the quantum state is postulated to collapse to $\vec\lambda$, in the non-degenerate case, or to $P_\lambda\psi\big/\! \sqrt$, in the general case. The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr–Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Newer interpretations of quantum mechanics have been formulated that do away with the concept of "wave function collapse" (see, for example, the many-worlds interpretation). The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wave functions become entangled so that the original quantum system ceases to exist as an independent entity (see ''Measurement in quantum mechanics'').

Time evolution of a quantum state

The time evolution of a quantum state is described by the Schrödinger equation:
$i\hbar \psi (t) =H \psi (t).$
Here $H$ denotes the Hamiltonian, the observable corresponding to the total energy of the system, and $\hbar$ is the reduced Planck constant. The constant $i\hbar$ is introduced so that the Hamiltonian is reduced to the classical Hamiltonian in cases where the quantum system can be approximated by a classical system; the ability to make such an approximation in certain limits is called the correspondence principle.

The solution of this differential equation is given by
$\psi(t) = e^\psi(0).$
The operator $U(t) = e^$ is known as the time-evolution operator, and has the crucial property that it is unitary. This time evolution is deterministic in the sense that – given an initial quantum state $\psi(0)$ – it makes a definite prediction of what the quantum state $\psi(t)$ will be at any later time.

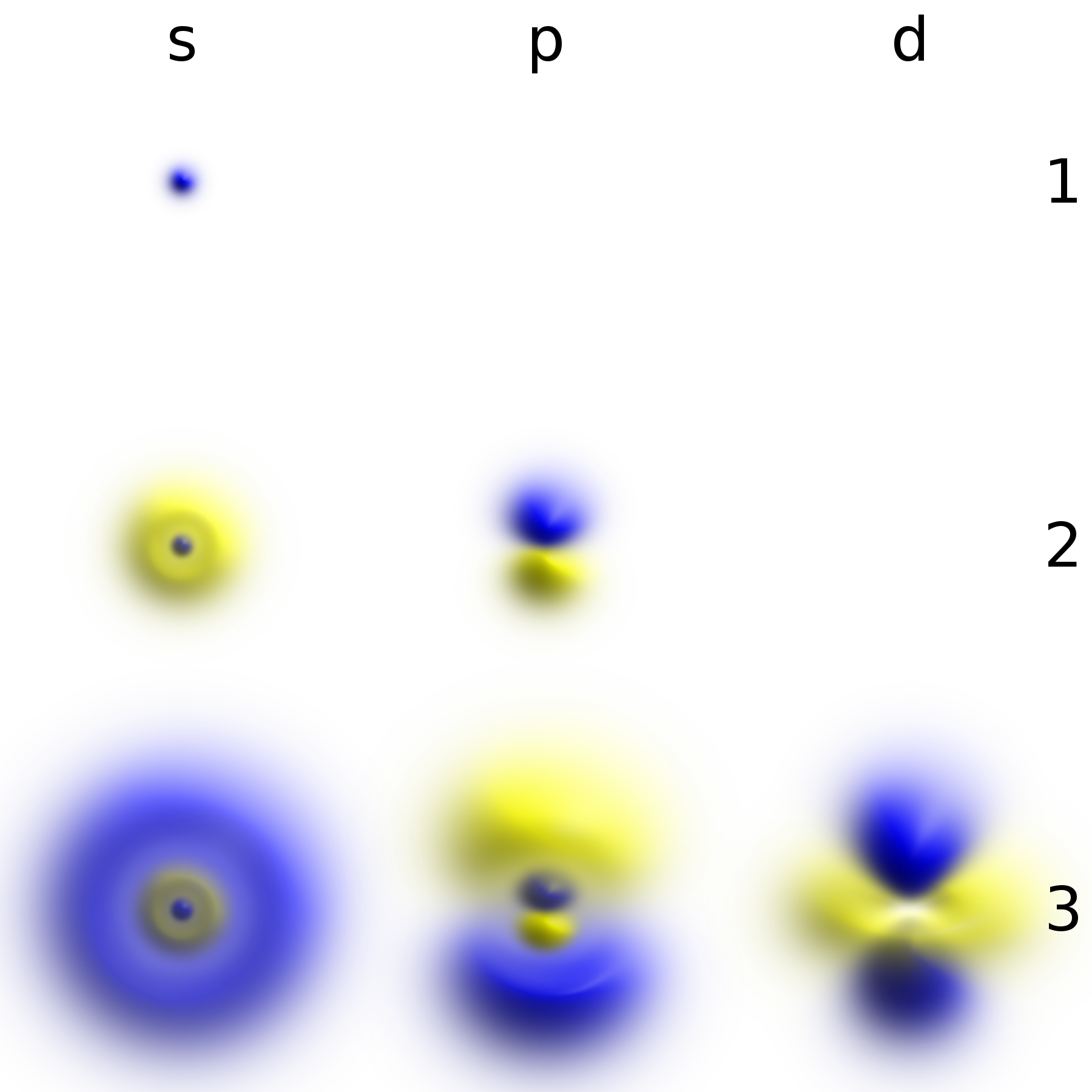
Some wave functions produce probability distributions that are independent of time, such as eigenstates of the Hamiltonian. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics, it is described by a static wave function surrounding the nucleus. For example, the electron wave function for an unexcited hydrogen atom is a spherically symmetric function known as an ''s'' orbital ( Fig. 1).

Analytic solutions of the Schrödinger equation are known for very few relatively simple model Hamiltonians including the quantum harmonic oscillator, the particle in a box, the dihydrogen cation, and the hydrogen atom. Even the helium atom – which contains just two electrons – has defied all attempts at a fully analytic treatment, admitting no solution in closed form.

However, there are techniques for finding approximate solutions. One method, called perturbation theory, uses the analytic result for a simple quantum mechanical model to create a result for a related but more complicated model by (for example) the addition of a weak potential energy. Another approximation method applies to systems for which quantum mechanics produces only small deviations from classical behavior. These deviations can then be computed based on the classical motion.

Uncertainty principle

One consequence of the basic quantum formalism is the uncertainty principle. In its most familiar form, this states that no preparation of a quantum particle can imply simultaneously precise predictions both for a measurement of its position and for a measurement of its momentum. Both position and momentum are observables, meaning that they are represented by Hermitian operators. The position operator $\hat$ and momentum operator $\hat$ do not commute, but rather satisfy the canonical commutation relation:
hat, \hat= i\hbar.
Given a quantum state, the Born rule lets us compute expectation values for both $X$ and $P$, and moreover for powers of them. Defining the uncertainty for an observable by a standard deviation, we have
$\sigma_X=,$
and likewise for the momentum:
$\sigma_P=\sqrt.$
The uncertainty principle states that
$\sigma_X \sigma_P \geq \frac.$
Either standard deviation can in principle be made arbitrarily small, but not both simultaneously.Section 3.2 of . This fact is experimentally well-known for example in quantum optics; see e.g. chap. 2 and Fig. 2.1 . This inequality generalizes to arbitrary pairs of self-adjoint operators $A$ and $B$. The commutator of these two operators is
$[A,B]=AB-BA,$
and this provides the lower bound on the product of standard deviations:
$\sigma_A \sigma_B \geq \tfrac12 \left, \bigl\langle[A,B]\bigr\rangle \.$

Another consequence of the canonical commutation relation is that the position and momentum operators are Fourier transform#Uncertainty principle, Fourier transforms of each other, so that a description of an object according to its momentum is the Fourier transform of its description according to its position. The fact that dependence in momentum is the Fourier transform of the dependence in position means that the momentum operator is equivalent (up to an $i/\hbar$ factor) to taking the derivative according to the position, since in Fourier analysis Fourier transform#Differentiation, differentiation corresponds to multiplication in the dual space. This is why in quantum equations in position space, the momentum $p_i$ is replaced by $-i \hbar \frac$, and in particular in the Schrödinger equation#Equation, non-relativistic Schrödinger equation in position space the momentum-squared term is replaced with a Laplacian times $-\hbar^2$.

Composite systems and entanglement

When two different quantum systems are considered together, the Hilbert space of the combined system is the tensor product of the Hilbert spaces of the two components. For example, let and be two quantum systems, with Hilbert spaces $\mathcal H_A$ and $\mathcal H_B$, respectively. The Hilbert space of the composite system is then
$\mathcal H_ = \mathcal H_A \otimes \mathcal H_B.$
If the state for the first system is the vector $\psi_A$ and the state for the second system is $\psi_B$, then the state of the composite system is
$\psi_A \otimes \psi_B.$
Not all states in the joint Hilbert space $\mathcal H_$ can be written in this form, however, because the superposition principle implies that linear combinations of these "separable" or "product states" are also valid. For example, if $\psi_A$ and $\phi_A$ are both possible states for system $A$, and likewise $\psi_B$ and $\phi_B$ are both possible states for system $B$, then
$\tfrac \left ( \psi_A \otimes \psi_B + \phi_A \otimes \phi_B \right )$
is a valid joint state that is not separable. States that are not separable are called quantum entanglement, entangled.

If the state for a composite system is entangled, it is impossible to describe either component system or system by a state vector. One can instead define reduced density matrix, reduced density matrices that describe the statistics that can be obtained by making measurements on either component system alone. This necessarily causes a loss of information, though: knowing the reduced density matrices of the individual systems is not enough to reconstruct the state of the composite system. Just as density matrices specify the state of a subsystem of a larger system, analogously, POVM, positive operator-valued measures (POVMs) describe the effect on a subsystem of a measurement performed on a larger system. POVMs are extensively used in quantum information theory.

As described above, entanglement is a key feature of models of measurement processes in which an apparatus becomes entangled with the system being measured. Systems interacting with the environment in which they reside generally become entangled with that environment, a phenomenon known as quantum decoherence. This can explain why, in practice, quantum effects are difficult to observe in systems larger than microscopic.

Equivalence between formulations

There are many mathematically equivalent formulations of quantum mechanics. One of the oldest and most common is the "transformation theory (quantum mechanics), transformation theory" proposed by Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics – matrix mechanics (invented by Werner Heisenberg) and wave mechanics (invented by Erwin Schrödinger). An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over all possible classical and non-classical paths between the initial and final states. This is the quantum-mechanical counterpart of the action principle in classical mechanics.

Symmetries and conservation laws

The Hamiltonian $H$ is known as the ''generator'' of time evolution, since it defines a unitary time-evolution operator $U(t) = e^$ for each value of $t$. From this relation between $U(t)$ and $H$, it follows that any observable $A$ that commutes with $H$ will be conserved: its expectation value will not change over time. This statement generalizes, as mathematically, any Hermitian operator $A$ can generate a family of unitary operators parameterized by a variable $t$. Under the evolution generated by $A$, any observable $B$ that commutes with $A$ will be conserved. Moreover, if $B$ is conserved by evolution under $A$, then $A$ is conserved under the evolution generated by $B$. This implies a quantum version of the result proven by Emmy Noether in classical (Lagrangian mechanics, Lagrangian) mechanics: for every differentiable Symmetry (physics), symmetry of a Hamiltonian, there exists a corresponding conservation law.

Examples

Free particle

The simplest example of a quantum system with a position degree of freedom is a free particle in a single spatial dimension. A free particle is one which is not subject to external influences, so that its Hamiltonian consists only of its kinetic energy:
$H = \fracP^2 = - \frac \frac .$
The general solution of the Schrödinger equation is given by
$\psi (x,t)=\frac \int _^\infty(k,0)e^\mathrmk,$
which is a superposition of all possible plane waves $e^$, which are eigenstates of the momentum operator with momentum $p = \hbar k$. The coefficients of the superposition are $\hat (k,0)$, which is the Fourier transform of the initial quantum state $\psi(x,0)$.

It is not possible for the solution to be a single momentum eigenstate, or a single position eigenstate, as these are not normalizable quantum states. Instead, we can consider a Gaussian wave packet:
$\psi(x,0) = \frace^$
which has Fourier transform, and therefore momentum distribution
$\hat \psi(k,0) = \sqrt[4]e^.$
We see that as we make $a$ smaller the spread in position gets smaller, but the spread in momentum gets larger. Conversely, by making $a$ larger we make the spread in momentum smaller, but the spread in position gets larger. This illustrates the uncertainty principle.

As we let the Gaussian wave packet evolve in time, we see that its center moves through space at a constant velocity (like a classical particle with no forces acting on it). However, the wave packet will also spread out as time progresses, which means that the position becomes more and more uncertain. The uncertainty in momentum, however, stays constant.

Particle in a box

The particle in a one-dimensional potential energy box is the most mathematically simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy everywhere inside a certain region, and therefore infinite potential energy everywhere outside that region. For the one-dimensional case in the $x$ direction, the time-independent Schrödinger equation may be written
$- \frac \frac = E \psi.$

With the differential operator defined by
$\hat_x = -i\hbar\frac$the previous equation is evocative of the Kinetic energy#Kinetic energy of rigid bodies, classic kinetic energy analogue,
$\frac \hat_x^2 = E,$
with state $\psi$ in this case having energy $E$ coincident with the kinetic energy of the particle.

The general solutions of the Schrödinger equation for the particle in a box are
$\psi(x) = A e^ + B e ^ \qquad\qquad E = \frac$
or, from Euler's formula,
$\psi(x) = C \sin(kx) + D \cos(kx).\!$

The infinite potential walls of the box determine the values of $C, D,$ and $k$ at $x=0$ and $x=L$ where $\psi$ must be zero. Thus, at $x=0$,
$\psi(0) = 0 = C\sin(0) + D\cos(0) = D$
and $D=0$. At $x=L$,
$\psi(L) = 0 = C\sin(kL),$
in which $C$ cannot be zero as this would conflict with the postulate that $\psi$ has norm 1. Therefore, since $\sin(kL)=0$, $kL$ must be an integer multiple of $\pi$,
$k = \frac\qquad\qquad n=1,2,3,\ldots.$

This constraint on $k$ implies a constraint on the energy levels, yielding
$E_n = \frac = \frac.$

A finite potential well is the generalization of the infinite potential well problem to potential wells having finite depth. The finite potential well problem is mathematically more complicated than the infinite particle-in-a-box problem as the wave function is not pinned to zero at the walls of the well. Instead, the wave function must satisfy more complicated mathematical boundary conditions as it is nonzero in regions outside the well. Another related problem is that of the rectangular potential barrier, which furnishes a model for the quantum tunneling effect that plays an important role in the performance of modern technologies such as flash memory and scanning tunneling microscopy.

Harmonic oscillator

As in the classical case, the potential for the quantum harmonic oscillator is given by
$V(x)=\fracm\omega^2x^2.$

This problem can either be treated by directly solving the Schrödinger equation, which is not trivial, or by using the more elegant "ladder method" first proposed by Paul Dirac. The eigenstates are given by
$\psi_n(x) = \sqrt \cdot \left(\frac\right)^ \cdot e^ \cdot H_n\left(\sqrt x \right), \qquad$
$n = 0,1,2,\ldots.$
where ''H_n'' are the Hermite polynomials
$H_n(x)=(-1)^n e^\frac\left(e^\right),$
and the corresponding energy levels are
$E_n = \hbar \omega \left(n + \right).$

This is another example illustrating the discretization of energy for bound states.

Mach–Zehnder interferometer

The Mach–Zehnder interferometer (MZI) illustrates the concepts of superposition and interference with linear algebra in dimension 2, rather than differential equations. It can be seen as a simplified version of the double-slit experiment, but it is of interest in its own right, for example in the delayed choice quantum eraser, the Elitzur–Vaidman bomb tester, and in studies of quantum entanglement.

We can model a photon going through the interferometer by considering that at each point it can be in a superposition of only two paths: the "lower" path which starts from the left, goes straight through both beam splitters, and ends at the top, and the "upper" path which starts from the bottom, goes straight through both beam splitters, and ends at the right. The quantum state of the photon is therefore a vector $\psi \in \mathbb^2$ that is a superposition of the "lower" path $\psi_l = \begin 1 \\ 0 \end$ and the "upper" path $\psi_u = \begin 0 \\ 1 \end$, that is, $\psi = \alpha \psi_l + \beta \psi_u$ for complex $\alpha,\beta$. In order to respect the postulate that $\langle \psi,\psi\rangle = 1$ we require that $, \alpha, ^2+, \beta, ^2 = 1$.

Both beam splitters are modelled as the unitary matrix $B = \frac1\begin 1 & i \\ i & 1 \end$, which means that when a photon meets the beam splitter it will either stay on the same path with a probability amplitude of $1/\sqrt$, or be reflected to the other path with a probability amplitude of $i/\sqrt$. The phase shifter on the upper arm is modelled as the unitary matrix $P = \begin 1 & 0 \\ 0 & e^ \end$, which means that if the photon is on the "upper" path it will gain a relative phase of $\Delta\Phi$, and it will stay unchanged if it is in the lower path.

A photon that enters the interferometer from the left will then be acted upon with a beam splitter $B$, a phase shifter $P$, and another beam splitter $B$, and so end up in the state
$BPB\psi_l = ie^ \begin -\sin(\Delta\Phi/2) \\ \cos(\Delta\Phi/2) \end,$
and the probabilities that it will be detected at the right or at the top are given respectively by
$p(u) = , \langle \psi_u, BPB\psi_l \rangle, ^2 = \cos^2 \frac,$
$p(l) = , \langle \psi_l, BPB\psi_l \rangle, ^2 = \sin^2 \frac.$
One can therefore use the Mach–Zehnder interferometer to estimate the Phase (waves), phase shift by estimating these probabilities.

It is interesting to consider what would happen if the photon were definitely in either the "lower" or "upper" paths between the beam splitters. This can be accomplished by blocking one of the paths, or equivalently by removing the first beam splitter (and feeding the photon from the left or the bottom, as desired). In both cases, there will be no interference between the paths anymore, and the probabilities are given by $p(u)=p(l) = 1/2$, independently of the phase $\Delta\Phi$. From this we can conclude that the photon does not take one path or another after the first beam splitter, but rather that it is in a genuine quantum superposition of the two paths.

Applications

Quantum mechanics has had enormous success in explaining many of the features of our universe, with regard to small-scale and discrete quantities and interactions which cannot be explained by Classical physics, classical methods. Quantum mechanics is often the only theory that can reveal the individual behaviors of the subatomic particles that make up all forms of matter (electrons, protons, neutrons, photons, and others). Solid-state physics and materials science are dependent upon quantum mechanics.

In many aspects, modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include quantum chemistry, quantum optics, quantum computing, superconducting magnets, light-emitting diodes, the optical amplifier and the laser, the transistor and semiconductors such as the microprocessor, medical imaging, medical and research imaging such as magnetic resonance imaging and electron microscopy. Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule DNA.

Relation to other scientific theories

Classical mechanics

The rules of quantum mechanics assert that the state space of a system is a Hilbert space and that observables of the system are Hermitian operators acting on vectors in that space – although they do not tell us which Hilbert space or which operators. These can be chosen appropriately in order to obtain a quantitative description of a quantum system, a necessary step in making physical predictions. An important guide for making these choices is the correspondence principle, a heuristic which states that the predictions of quantum mechanics reduce to those of classical mechanics in the regime of large quantum numbers. One can also start from an established classical model of a particular system, and then try to guess the underlying quantum model that would give rise to the classical model in the correspondence limit. This approach is known as Canonical quantization, quantization.

When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was theory of relativity, non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the harmonic oscillator, classical harmonic oscillator.

Complications arise with chaotic systems, which do not have good quantum numbers, and quantum chaos studies the relationship between classical and quantum descriptions in these systems.

Quantum decoherence is a mechanism through which quantum systems lose quantum coherence, coherence, and thus become incapable of displaying many typically quantum effects: quantum superpositions become simply probabilistic mixtures, and quantum entanglement becomes simply classical correlations. Quantum coherence is not typically evident at macroscopic scales, though at temperatures approaching absolute zero quantum behavior may manifest macroscopically.

Many macroscopic properties of a classical system are a direct consequence of the quantum behavior of its parts. For example, the stability of bulk matter (consisting of atoms and molecules which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of electric charges under the rules of quantum mechanics.

Special relativity and electrodynamics

Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein–Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field (rather than a fixed set of particles). The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction. Quantum electrodynamics is, along with general relativity, one of the most accurate physical theories ever devised.

The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one that has been used since the inception of quantum mechanics, is to treat electric charge, charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical $\textstyle -e^2/(4 \pi\epsilon_r)$ Electric potential, Coulomb potential. Likewise, in a Stern–Gerlach experiment, a charged particle is modeled as a quantum system, while the background magnetic field is described classically. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.

Field (physics), Quantum field theories for the strong nuclear force and the weak nuclear force have also been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of subnuclear particles such as quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory (known as electroweak theory), by the physicists Abdus Salam, Sheldon Glashow and Steven Weinberg.

Relation to general relativity

Even though the predictions of both quantum theory and general relativity have been supported by rigorous and repeated empirical evidence, their abstract formalisms contradict each other and they have proven extremely difficult to incorporate into one consistent, cohesive model. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those particular applications. However, the lack of a correct theory of quantum gravity is an important issue in physical cosmology and the search by physicists for an elegant "Theory of Everything" (TOE). Consequently, resolving the inconsistencies between both theories has been a major goal of 20th- and 21st-century physics. This TOE would combine not only the models of subatomic physics but also derive the four fundamental forces of nature from a single force or phenomenon.

One proposal for doing so is string theory, which posits that the Point particle, point-like particles of particle physics are replaced by Dimension (mathematics and physics), one-dimensional objects called String (physics), strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge (physics), charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries gravitational force.

Another popular theory is loop quantum gravity (LQG), which describes quantum properties of gravity and is thus a theory of quantum spacetime. LQG is an attempt to merge and adapt standard quantum mechanics and standard general relativity. This theory describes space as an extremely fine fabric "woven" of finite loops called spin networks. The evolution of a spin network over time is called a spin foam. The characteristic length scale of a spin foam is the Planck length, approximately 1.616×10⁻³⁵ m, and so lengths shorter than the Planck length are not physically meaningful in LQG.

Philosophical implications

Since its inception, the many counter-intuitive aspects and results of quantum mechanics have provoked strong philosophical debates and many interpretations of quantum mechanics, interpretations. The arguments centre on the probabilistic nature of quantum mechanics, the difficulties with wavefunction collapse and the related measurement problem, and quantum nonlocality. Perhaps the only consensus that exists about these issues is that there is no consensus. Richard Feynman once said, "I think I can safely say that nobody understands quantum mechanics." According to Steven Weinberg, "There is now in my opinion no entirely satisfactory interpretation of quantum mechanics."

The views of Niels Bohr, Werner Heisenberg and other physicists are often grouped together as the "Copenhagen interpretation". According to these views, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but is instead a final renunciation of the classical idea of "causality". Bohr in particular emphasized that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the complementarity (physics), complementary nature of evidence obtained under different experimental situations. Copenhagen-type interpretations were adopted by Nobel laureates in quantum physics, including Bohr, Heisenberg, Schrödinger, Feynman, and Anton Zeilinger, Zeilinger as well as 21st-century researchers in quantum foundations.

Albert Einstein, himself one of the founders of Old quantum theory, quantum theory, was troubled by its apparent failure to respect some cherished metaphysical principles, such as determinism and principle of locality, locality. Einstein's long-running exchanges with Bohr about the meaning and status of quantum mechanics are now known as the Bohr–Einstein debates. Einstein believed that underlying quantum mechanics must be a theory that explicitly forbids action at a distance. He argued that quantum mechanics was incomplete, a theory that was valid but not fundamental, analogous to how thermodynamics is valid, but the fundamental theory behind it is statistical mechanics. In 1935, Einstein and his collaborators Boris Podolsky and Nathan Rosen published an argument that the principle of locality implies the incompleteness of quantum mechanics, a thought experiment later termed the Einstein–Podolsky–Rosen paradox. In 1964, John Stewart Bell, John Bell showed that EPR's principle of locality, together with determinism, was actually incompatible with quantum mechanics: they implied constraints on the correlations produced by distance systems, now known as Bell inequalities, that can be violated by entangled particles. Since then Bell test, several experiments have been performed to obtain these correlations, with the result that they do in fact violate Bell inequalities, and thus falsify the conjunction of locality with determinism.

Bohmian mechanics shows that it is possible to reformulate quantum mechanics to make it deterministic, at the price of making it explicitly nonlocal. It attributes not only a wave function to a physical system, but in addition a real position, that evolves deterministically under a nonlocal guiding equation. The evolution of a physical system is given at all times by the Schrödinger equation together with the guiding equation; there is never a collapse of the wave function. This solves the measurement problem.

Everett's many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a multiverse composed of mostly independent parallel universes. This is a consequence of removing the axiom of the collapse of the wave packet. All possible states of the measured system and the measuring apparatus, together with the observer, are present in a real physical quantum superposition. While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we do not observe the multiverse as a whole, but only one parallel universe at a time. Exactly how this is supposed to work has been the subject of much debate. Several attempts have been made to make sense of this and derive the Born rule, with no consensus on whether they have been successful.

Relational quantum mechanics appeared in the late 1990s as a modern derivative of Copenhagen-type ideas, and QBism was developed some years later.

History

Quantum mechanics was developed in the early decades of the 20th century, driven by the need to explain phenomena that, in some cases, had been observed in earlier times. Scientific inquiry into the wave nature of light began in the 17th and 18th centuries, when scientists such as Robert Hooke, Christiaan Huygens and Leonhard Euler proposed a wave theory of light based on experimental observations. In 1803 English polymath Thomas Young (scientist), Thomas Young described the famous Young's interference experiment, double-slit experiment. This experiment played a major role in the general acceptance of the wave theory of light.

During the early 19th century, chemistry, chemical research by John Dalton and Amedeo Avogadro lent weight to the atomic theory of matter, an idea that James Clerk Maxwell, Ludwig Boltzmann and others built upon to establish the kinetic theory of gases. The successes of kinetic theory gave further credence to the idea that matter is composed of atoms, yet the theory also had shortcomings that would only be resolved by the development of quantum mechanics. Reprinted, Addison-Wesley, 1989, While the early conception of atoms from Greek philosophy had been that they were indivisible unitsthe word "atom" deriving from the Greek language, Greek for 'uncuttable'the 19th century saw the formulation of hypotheses about subatomic structure. One important discovery in that regard was Michael Faraday's 1838 observation of a glow caused by an electrical discharge inside a glass tube containing gas at low pressure. Julius Plücker, Johann Wilhelm Hittorf and Eugen Goldstein carried on and improved upon Faraday's work, leading to the identification of cathode rays, which J. J. Thomson found to consist of subatomic particles that would be called electrons.

The black-body radiation problem was discovered by Gustav Kirchhoff in 1859. In 1900, Max Planck proposed the hypothesis that energy is radiated and absorbed in discrete "quanta" (or energy packets), yielding a calculation that precisely matched the observed patterns of black-body radiation. The word ''quantum'' derives from the Latin, meaning "how great" or "how much". According to Planck, quantities of energy could be thought of as divided into "elements" whose size (''E'') would be proportional to their frequency (''ν''):
$E = h \nu\$,
where ''h'' is the Planck constant. Planck cautiously insisted that this was only an aspect of the processes of absorption and emission of radiation and was not the physical reality of the radiation. In fact, he considered his quantum hypothesis a mathematical trick to get the right answer rather than a sizable discovery. However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis local realism, realistically and used it to explain the photoelectric effect, in which shining light on certain materials can eject electrons from the material. Niels Bohr then developed Planck's ideas about radiation into a Bohr model, model of the hydrogen atom that successfully predicted the spectral lines of hydrogen. Einstein further developed this idea to show that an electromagnetic wave such as light could also be described as a particle (later called the photon), with a discrete amount of energy that depends on its frequency. In his paper "On the Quantum Theory of Radiation", Einstein expanded on the interaction between energy and matter to explain the absorption and emission of energy by atoms. Although overshadowed at the time by his general theory of relativity, this paper articulated the mechanism underlying the stimulated emission of radiation, which became the basis of the laser.

This phase is known as the old quantum theory. Never complete or self-consistent, the old quantum theory was rather a set of heuristic corrections to classical mechanics. The theory is now understood as a WKB approximation#Application to the Schrödinger equation, semi-classical approximation to modern quantum mechanics. Notable results from this period include, in addition to the work of Planck, Einstein and Bohr mentioned above, Einstein and Peter Debye's work on the specific heat of solids, Bohr and Hendrika Johanna van Leeuwen's Bohr–Van Leeuwen theorem, proof that classical physics cannot account for diamagnetism, and Arnold Sommerfeld's extension of the Bohr model to include special-relativistic effects.

In the mid-1920s quantum mechanics was developed to become the standard formulation for atomic physics. In 1923, the French physicist Louis de Broglie put forward his theory of matter waves by stating that particles can exhibit wave characteristics and vice versa. Building on de Broglie's approach, modern quantum mechanics was born in 1925, when the German physicists Werner Heisenberg, Max Born, and Pascual JordanDavid Edwards, "The Mathematical Foundations of Quantum Mechanics", ''Synthese'', Volume 42, Number 1/September, 1979, pp. 1–70.David Edwards, "The Mathematical Foundations of Quantum Field Theory: Fermions, Gauge Fields, and Super-symmetry, Part I: Lattice Field Theories", ''International Journal of Theoretical Physics'', Vol. 20, No. 7 (1981). developed matrix mechanics and the Austrian physicist Erwin Schrödinger invented Schrödinger equation, wave mechanics. Born introduced the probabilistic interpretation of Schrödinger's wave function in July 1926. Thus, the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth Solvay Conference in 1927.

By 1930, quantum mechanics had been further unified and formalized by David Hilbert, Paul Dirac and John von Neumann with greater emphasis on measurement in quantum mechanics, measurement, the statistical nature of our knowledge of reality, and Interpretations of quantum mechanics, philosophical speculation about the 'observer'. It has since permeated many disciplines, including quantum chemistry, quantum electronics, quantum optics, and quantum information science. It also provides a useful framework for many features of the modern periodic table of elements, and describes the behaviors of atoms during chemical bonding and the flow of electrons in computer semiconductors, and therefore plays a crucial role in many modern technologies. While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some macroscopic phenomena such as superconductors and superfluids.

See also

* Bra–ket notation
* Einstein's thought experiments
* List of textbooks on classical mechanics and quantum mechanics
* Macroscopic quantum phenomena
* Phase-space formulation
* Regularization (physics)
* Two-state quantum system

Explanatory notes

References

Further reading

The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus:
* Marvin Chester, Chester, Marvin (1987). ''Primer of Quantum Mechanics''. John Wiley.
*
* Richard Feynman, 1985. ''QED: The Strange Theory of Light and Matter'', Princeton University Press. . Four elementary lectures on quantum electrodynamics and quantum field theory, yet containing many insights for the expert.
* Giancarlo Ghirardi, Ghirardi, GianCarlo, 2004. ''Sneaking a Look at God's Cards'', Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
* N. David Mermin, 1990, "Spooky actions at a distance: mysteries of the QT" in his ''Boojums All the Way Through''. Cambridge University Press: 110–76.
* Victor Stenger, 2000. ''Timeless Reality: Symmetry, Simplicity, and Multiple Universes''. Buffalo, New York: Prometheus Books. Chpts. 5–8. Includes cosmological and philosophical considerations.

More technical:
*
*
*
*
* Bryce DeWitt, R. Neill Graham, eds., 1973. ''The Many-Worlds Interpretation of Quantum Mechanics'', Princeton Series in Physics, Princeton University Press.
*
*
* Daniel Greenberger, D. Greenberger, Klaus Hentschel, K. Hentschel, F. Weinert, eds., 2009. ''Compendium of quantum physics, Concepts, experiments, history and philosophy'', Springer-Verlag, Berlin, Heidelberg. Short articles on many QM topics.
* A standard undergraduate text.
* Max Jammer, 1966. ''The Conceptual Development of Quantum Mechanics''. McGraw Hill.
* Hagen Kleinert, 2004. ''Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets'', 3rd ed. Singapore: World Scientific
Draft of 4th edition.

*
Online copy
*
* Gunther Ludwig, 1968. ''Wave Mechanics''. London: Pergamon Press.
* George Mackey (2004). ''The mathematical foundations of quantum mechanics''. Dover Publications. .
*
* Albert Messiah, 1966. ''Quantum Mechanics'' (Vol. I), English translation from French by G. M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III
online
*
* Considers the extent to which chemistry and the periodic system have been reduced to quantum mechanics.
*
*
*
*
* Martinus J. G. Veltman, Veltman, Martinus J. G. (2003), ''Facts and Mysteries in Elementary Particle Physics''.

External links

Introduction to Quantum Theory at Quantiki.

Quantum Physics Made Relatively Simple
three video lectures by Hans Bethe.

Course material

Quantum Cook Book
an
PHYS 201: Fundamentals of Physics II
by Ramamurti Shankar, Yale OpenCourseware.
*
Modern Physics: With waves, thermodynamics, and optics
' – an online textbook.
* MIT OpenCourseWare
Chemistry
an
Physics
Se
8.04
an



Examples in Quantum Mechanics

Philosophy
*
*

{{Authority control

Quantum mechanics,