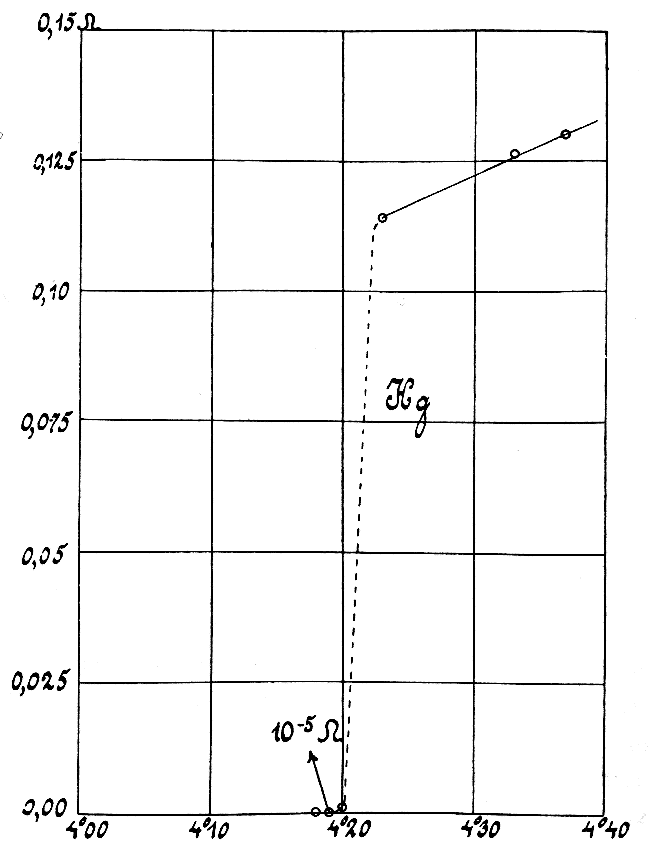
|
Potential Barrier
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left. Although classically a particle behaving as a point mass would be reflected if its energy is less than a particle actually behaving as a matter wave has a non-zero probability of penetrating the barrier and continuing its travel as a wave on the other side. In classical wave-physics, this effect is known as evanescent wave coupling. The likelihood that the particle will pass through the barrier is given by the transmission coefficient, whereas the likelihood that it is reflected is given by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Step Potential
In quantum mechanics and scattering theory, the one-dimensional step potential is an idealized system used to model incident, reflected and transmitted matter waves. The problem consists of solving the time-independent Schrödinger equation for a particle with a step-like potential in one dimension. Typically, the potential is modeled as a Heaviside step function. Calculation Schrödinger equation and potential function The time-independent Schrödinger equation for the wave function \psi(x) is \hat H\psi(x) = \left[-\frac \frac + V(x)\right]\psi(x) = E\psi(x), where ''Ĥ'' is the Hamiltonian (quantum mechanics), Hamiltonian, ''ħ'' is the reduced Planck constant, ''m'' is the mass, ''E'' the energy of the particle. The step potential is simply the product of ''V''0, the height of the barrier, and the Heaviside step function: V(x) = \begin 0, & x < 0 \\ V_0, & x \ge 0 \end The barrier is positioned at ''x'' = 0, though any position ''x''0 may be chosen w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morse/Long-range Potential
The Morse/Long-range potential (MLR potential) is an interatomic interaction model for the potential energy of a diatomic molecule. Due to the simplicity of the regular Morse potential (it only has three adjustable parameters), it is very limited in its applicability in modern spectroscopy. The MLR potential is a modern version of the Morse potential which has the correct theoretical long-range form of the potential naturally built into it. It has been an important tool for spectroscopists to represent experimental data, verify measurements, and make predictions. It is useful for its extrapolation capability when data for certain regions of the potential are missing, its ability to predict energies with accuracy often better than the most sophisticated ''ab initio'' techniques, and its ability to determine precise empirical values for physical parameters such as the dissociation energy, equilibrium bond length, and long-range constants. Cases of particular note include: # the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Potential Barrier (QM)
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential. The delta potential well is a limiting case of the finite potential well, which is obtained if one maintains the product of the width of the well and the potential constant while decreasing the well's width and increasing the potential. This article, for simplicity, only considers a one-dimensional potential well, but analysis could be expanded t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Of Variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary differential equation, ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation. Ordinary differential equations (ODE) A differential equation for the unknown f(x) is separable if it can be written in the form :\frac f(x) = g(x)h(f(x)) where g and h are given functions. This is perhaps more transparent when written using y = f(x) as: :\frac=g(x)h(y). So now as long as ''h''(''y'') ≠ 0, we can rearrange terms to obtain: : = g(x) \, dx, where the two variables ''x'' and ''y'' have been separated. Note ''dx'' (and ''dy'') can be viewed, at a simple level, as just a convenient notation, which provides a handy mnemonic aid for assisting with manipulations. A formal definition of ''dx'' as a differential (infinitesimal) is somewhat advanced. Al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scanning Tunneling Microscope
A scanning tunneling microscope (STM) is a type of scanning probe microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in Physics in 1986. STM senses the surface by using an extremely sharp conducting tip that can distinguish features smaller than 0.1 nm with a 0.01 nm (10 pm) depth resolution. This means that individual atoms can routinely be imaged and manipulated. Most scanning tunneling microscopes are built for use in ultra-high vacuum at temperatures approaching absolute zero, but variants exist for studies in air, water and other environments, and for temperatures over 1000 °C. STM is based on the concept of quantum tunneling. When the tip is brought very near to the surface to be examined, a bias voltage applied between the two allows electrons to tunnel through the vacuum separating them. The resulting ''tunneling current'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Mass (solid-state Physics)
In solid state physics, a particle's effective mass (often denoted m^*) is the mass that it ''seems'' to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors. For electrons or electron holes in a solid, the effective mass is usually stated as a factor multiplying the rest mass of an electron, ''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek alphabet, Greek letter (Rho (letter), rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the Electrical resistance, resistance between these contacts is , then the resistivity of the material is . Electrical conductivity (or specific conductance) is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter (Sigma (letter), sigma), but (kappa) (especially in electrical engineering) and (gamma) are sometimes used. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
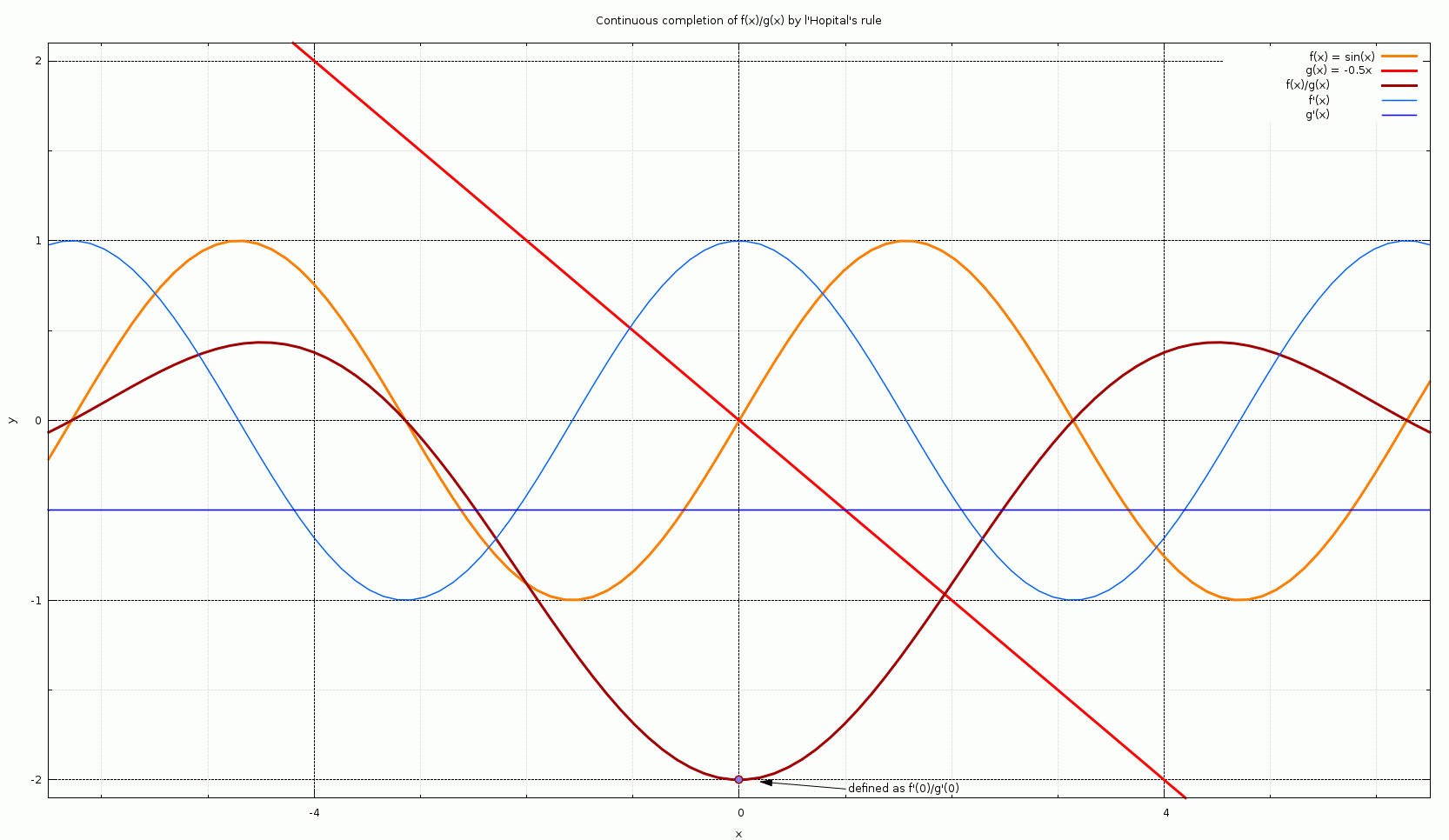
L'Hôpital's Rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli. L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on I\setminus \ for a (possibly infinite) accumulation point of , if \lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty, and g'(x)\ne 0 for all in I\setminus \, and \lim \limits_\frac exists, then :\lim_\frac = \lim_\frac. The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Function
Although the function is not defined at zero, as becomes closer and closer to zero, becomes arbitrarily close to 1. In other words, the limit of as approaches zero, equals 1. In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function. Formal definitions, first devised in the early 19th century, are given below. Informally, a function assigns an output to every input . We say that the function has a limit at an input , if gets closer and closer to as moves closer and closer to . More specifically, the output value can be made ''arbitrarily'' close to if the input to is taken ''sufficiently'' close to . On the other hand, if some inputs very close to are taken to outputs that stay a fixed distance apart, then we say the limit ''does not exist''. The notion of a limit has many applications in modern calc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |